
- •Тема V. : ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
- •Тема V: ЭЛЕМЕНТЫ
- •Введение. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПОЛЕ.
- •Глава I. Криволинейные интегралы.
- •где – дифференциал дуги. Функция
- •Свойства криволинейного интеграла совпадают со свойствами
- •§2. Вычисление криволинейных интегралов 1-го рода.
- •в) если кривая задана уравнением ( ) ( 1 2 ), то dl
- •Пример 1. Вычислить L xdl-y по отрезку прямой, соединяющему
- •Пример 2. Вычислить
- •§3. Криволинейные интегралы 2-го рода (по координатам).
- •Криволинейный интеграл от непрерывной в некоторой области
- •§4. Вычисление криволинейных интегралов 2-го рода.
- •Замечания. В случае замкнутой кривой берется направление
- •Пример. Вычислить
- •§5. Криволинейные интегралы 2-го рода по замкнутому контуру. Формула Грина.
- •п р е д е л е н и е. Циркуляцией векторного поля
- •5.2. Формула Грина. - устанавливает связь между криволинейными и
- •Найти циркуляцию векторного поля
- •§6. Условие независимости криволинейного интеграла 2-го рода от пути интегрирования .
- •Таким образом, в некоторых случаях величина криволинейного интеграла не зависит от пути интегрирования,
- •Замечание 1. На практике для проверки независимости интеграла от пути интегрирования проверяют условие

Тема V. : ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА |
Преподаватель:
Филипенко Николай Максимович
Доцент ОМИ
Тема V: ЭЛЕМЕНТЫ
ВЕКТОРНОГО АНАЛИЗА.
Криволинейные и поверхностные интегралы.
Лекция 1

Введение. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПОЛЕ.
Изучаемые в физике величины можно разделить на два вида: скалярные и векторные. Скалярными называют величины, характеризуемые одним числом – масса, энергия, температура, а векторные величины характеризуются как своим числовым значением, так и направлением в пространстве – сила, скорость. Скалярные и векторные величины могут быть функциями
координат точек пространства и времени. В этом случае их называют скалярными и векторными полями.
Определение. В пространстве задано поле некоторой величины, если в каждой точке пространства или некоторой его области определено значение этой величины U=f(x,y,z) или F=F(x,y,z).
Поля бывают стационарными, плоскими, нестационарными. Ранее для стационарного скалярного поля (не определяя его как
поле), мы ввели понятия производной по направлению и градиента для скалярного поля U=f(x,y,z):
Направление вектора-градиента при этом есть направление, в котором поле растет с наибольшей
скоростью. Скалярное поле U=f(x,y,z), образует вполне определенное векторное поле - градиент.
Характеристиками векторных полей являются: Поток (П), циркуляция (Ц), дивергенция и ротор, которые выражаются
через криволинейные и поверхностные интегралы.
Глава I. Криволинейные интегралы.
§1. Криволинейные интегралы 1-го рода (по длине дуги)
Схема построения криволинейного интеграла первого рода
аналогична схеме построения определенного интеграла. Пусть непрерывная функция z f (x; y) задана на непрерывной кривой L,
лежащей в плоскости x0y . Разобъем линию интегрирования на элементарные части li , вычислим значения функции в произвольной
точке каждого элементарного участка кривой и умножим значения функции в точках кривой на длины соответствующих элементарных дуг. Сумма таких произведений
n
f xi ; yi li
i 1
называется интегральной суммой.
Криволинейным интегралом первого рода от функции z f (x; y)
по кривой L называется предел интегральных сумм при условии max li 0, т. е. при неограниченном увеличении числа элементарных
частей, когда все элементарные участки стягиваются в точку:
|
|
f (x; y)dl lim f (xi ; yi ) li . |
|
L |
n n 1 |

где – дифференциал дуги. Функция
называется интегрируемой вдоль кривой L (AB), сама кривая (L) – контуром интегрирования; А – начальной, B
– конечной точкой интегрирования. Аналогично можно ввести криволинейный интеграл по пространственной кривой для функции 3-х переменных f(x,y,z).
Для существования криволинейного интеграла необходимо и достаточно, чтобы функция f(x,y) была непрерывна вдоль кривой АВ , а кривая АВ была «гладкой» или «кусочно-гладкой».
Определение Кривая, заданная уравнениями: x=φ(t); y=ψ(t), называется гладкой, если функции φ(t) и ψ(t) непрерывны и имеют производные, которые не обращаются в нуль одновременно (есть касательная). Непрерывная кривая, составленная из конечного числа «гладких кусков», называется «кусочно-гладкой».

Свойства криволинейного интеграла совпадают со свойствами
определенного интеграла (вынос постоянного множителя, почленное интегрирование, разбиение линии интегрирования на части).
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла.
Геометрически криволинейный интеграл первого рода от неотрицательной функции f (x; y) вдоль контура L есть площадь
цилиндрической поверхности (рис.)
Sцил.пов f (x; y)dl ,
L
если же подынтегральная функция f (x; y) 1, то криволинейный интеграл от элемента дуги dl есть длина кривой L:
dl .
L

§2. Вычисление криволинейных интегралов 1-го рода.
Для вычисления криволинейного интеграла по длине дуги используется одна из следующих формул:
а) если кривая задана уравнением |
|
|
|
y (x)(a x b), то |
|
|||||||||||
|
dl |
|
|
|
|
dx |
|
|
|
|
|
|||||
|
1 x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
dx; |
(2.1) |
|||
f (x; y)dl f (x; (x)) |
1 |
|
|
|
||||||||||||
(x) |
|
|||||||||||||||
L |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) если кривая задана параметрически |
|
|
|
|
|
|
|
|
||||||||
|
x x(t), |
y y(t) |
|
|
|
( t ) , то |
|
|||||||||
|
dl |
|
|
dt |
|
|
|
|
|
|||||||
|
xt' 2 yt' 2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xt' 2 yt' 2 dt ; |
(2.2) |
|||||||||
f (x; y)dl f (x(t), y(t)) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

в) если кривая задана уравнением ( ) ( 1 2 ), то dl 
 2 2 d
2 2 d
2 |
|
|
|
|
|
|
|
|
2 |
|
2 |
d . |
|||
f (x; y)dl f ( cos , sin ) |
|
||||||
|
( ) |
|
|||||
L 1
Замечания. Кривая в пространстве обычно задается параметрически:
|
x x(t), y y(t), z z(t), |
( t ) |
||
|
|
|
|
|
|
xt' |
2 yt' 2 zt' 2 dt . |
||
f (x; y; z)dl f (x(t); y(t); z(t)) |
||||
|
|
|
|
|
L |
|
|
|
|
г) Если АВ – не кривая, а отрезок прямой, с А – начальной, B – конечной точкой, расположенный параллельно оси 0Х, то f(x,y)=f(x,y0) и dl=dx, а криволинейный интеграл будет обычным определенным интегралом.
(2.3)
(2.4)

Пример 1. Вычислить L xdl-y по отрезку прямой, соединяющему
точки A(0; 2) и B(4; 0) .
Решение. Данный интеграл – криволинейный интеграл по длине дуги (первого рода).
Для данного интеграла запишем уравнение прямой, проходящей
через две точки: |
|
|
|
|
|
|
|
|
x 0 |
|
|
y 2 |
|
|
1 x 2. |
||||||||||||||
|
x xA |
|
y yA |
, |
|
|
|
y |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 2 |
||||||||||||||||||
|
xB xA |
yB yA |
|
4 0 |
|
|
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||
Для данной линии dl 1 |
|
|
dx |
|
|
|
|
|
|
|
|
dx. |
|
|
|||||||||||||||
|
|
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При движении от A к B x меняется от 0 до 4. По формуле (73) |
|||||||||||||||||||||||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
dl |
|
|
|
4 |
|
|
dx |
|
|
|
|
|
|
|
|
4 |
dx |
|
|
||||||||
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|||||||||||||||||
|
L x y |
|
0 x 0,5x 2 |
|
0 0,5x 2 |
||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||

 5 ln 0,5x 2 4
5 ln 0,5x 2 4
0

 5 ln 4 ln 2
5 ln 4 ln 2 
 5 ln 2.
5 ln 2.
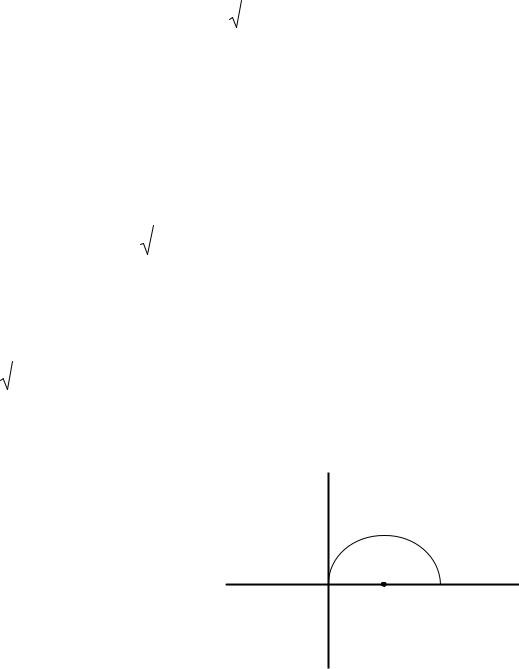
Пример 2. Вычислить |
|
|
x2 |
y2 |
dl , где L – верхняя половина |
||||||||||||||
|
|
x2 y2 ax |
|
L |
|
|
|
|
|
|
|
|
|||||||
окружности |
(a 0) (см. рис.). Перейдем |
к полярным |
|||||||||||||||||
координатам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x cos , |
y sin , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 y2 ax 2 cos2 2 sin 2 a cos , |
|
||||||||||||||||||
2 cos2 sin 2 a cos |
или |
|
acos , |
|
|||||||||||||||
' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
dl a |
2 |
cos |
2 |
a |
2 |
sin |
2 |
d ad . |
|
||||||||
asin |
|
|
|
|
|
|
|||||||||||||
Так как берется только верхняя часть окружности, то угол |
|||||||||||||||||||
меняется от 0 до |
. По формуле (2.2) имеем |
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dl 2 ad a2 |
2 cos d a2 sin |
|
||||||||||||||
|
|
2 a2 |
0 a2. |
||||||||||||||||
|
x2 y2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
L |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y
0 |
a |
a |
x |
|
2 |
||||
|
|
|
Рис.

|
Пример 3. Вычислить |
|
x2 |
y2 |
dl , где L – дуга |
|
|
|
|||||||||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a cost t sin t , |
y a(sin t t cost) |
(0 t 2 ). |
|||||||||||||||||||
|
Решение. Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
dl |
xt' 2 yt' 2 |
dt |
|
|
|
|
|
|
||||||||||
|
|
a sin t sin t t cost 2 |
a cost cost t sin t 2 |
dt |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a2t2 cos2 t a2t2 sin2 tdt at dt, |
|
|
|
|||||||||||||||||
то по формуле (2.2) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x2 |
y2 |
dl |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a2 cos2 t 2t sin t cost t2 sin2 t sin2 t 2t sin t cost t2 cos2 t atdt |
|||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 1 |
|
2 |
2 |
2 |
|
3 |
|
3 |
|
|
|||||||
|
|
1 t2tdt a2 1 |
|
a |
|
||||||||||||||||||
|
a |
t |
|
|
|
|
|
1 4 2 2 |
1 . |
||||||||||||||
0 |
2 |
|
|
|
|
3 |
|
|
|
|
0 |
|
3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||



