
- •Тема1: Неопределенный интеграл
- •Глава I. Понятие и свойства неопределенного интеграла.
- •Глава III. Методы и приемы интегрирования некоторых классов функций.
- •§1. Интегрирование рациональных дробей методом неопределенных коэффициентов
- •Схема интегрирования правильной рациональной дроби.
- •Примеры разложения дробей на сумму простейших дробей
- •Рассмотрим примеры.
- •§2. Интегрирование тригонометрических функций. 1.Универсальная тригонометрическая подстановка
- •2.Тангенциальная подстановка
- •4. Интегрирование тригонометрических функций
- •5. При решении интегралов применяются некоторые искусственные приемы, например
- •Интегрирование тригонометрических выражений
- •§3. Интегрирование иррациональных функций.
- •следующих примерах для того, чтобы избавиться т иррациональности применяются тригонометрические подстановк ри этом
- •Интегрирование иррациональных выражений
- •Интегрирование иррациональных выражений
- •Интегрирование иррациональных выражений
- •Не берущиеся интегралы

§2. Интегрирование тригонометрических функций. 1.Универсальная тригонометрическая подстановка
|
x |
|
x = 2arctg t, |
dx = |
2 |
dt; |
|
1 |
t2 |
|
|
2t |
||
tg |
|
= t |
|
cos x = |
|
|
, |
sin x = |
|
. |
||||
|
|
1 t2 |
|
|
||||||||||
2 |
|
1 |
t2 |
1 t2 |
||||||||||
С помощью универсальной подстановки находятся интегралы вида
|
|
|
|
dx |
|
|
|
|
|
, |
|
|
dx |
, |
|
|
|
dx |
|
|
|
|
, |
|
|
|
|
|
|
|
sin x dx |
2 |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
asin x bcos x c |
|
|
|
cos x |
|
|
|
2cos x 5 |
|
|
|
|
|
|
|
(3sin x 2) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
tg |
x |
= t, dx = |
2dt |
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1. |
|
= |
|
|
2 |
|
|
2t |
|
|
1 t |
2 |
|
|
= |
|
|
|
|
|
|
= |
|
|
= |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
2 |
|
8t 2 |
||||||||||||||||||||||||||||||||||||
|
|
|
2 4sin x |
|
|
sin x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 4 |
|
|
|
|
2t |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
dt |
|
|
dt |
|
|
|
|
|
1 |
|
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
tg(x/2) |
2 |
|
|
|
|
|||||||||||||
= |
|
|
= |
|
|
|
|
= |
|
|
ln |
|
3 |
|
|
|
= |
|
|
|
|
|
|
|
ln |
|
3 |
|
|
c |
|||||||||||||||||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4t |
1 |
2) |
3 |
2 3 |
t |
2 |
3 |
|
2 |
|
|
3 |
|
tg(x/2) |
2 |
3 |
|||||||||||||||||||||||||||||||||||||
t |
|
(t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
x |
= t |
|
|
cos x = |
|
1 |
t2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
2 |
|
|
|
1 t |
2 |
|
= |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
5sin x |
|
2cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
dx = |
|
|
|
|
sin x = |
|
2t |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t2 |
|
|
1 t2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
2 dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|||||||||
= |
|
|
|
1 t2 |
|
|
|
|
|
|
|
2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
== 2 |
|
|
|
= |
||||||||||||||||||||
|
|
2t |
|
|
|
|
1 |
t |
|
t |
2 |
) 10t |
|
2(1 |
t |
2 |
) |
2 |
|
|
10t 5 |
|||||||||||||||||||||||||||||||||
|
3 5 |
|
|
|
2 |
|
|
|
|
|
|
|
|
3(1 |
|
|
|
|
|
t |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 t2 |
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
dt |
|
|
|
|
= 2 |
|
|
1 |
|
|
ln | |
(t |
5) |
|
|
|
|
20 |
|
|
|
|= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5) |
2 |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
20 |
|
(t |
5) |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
(t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
tg |
|
5 |
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
ln | |
2 |
|
|
|
|
|
| C. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
5 |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

2.Тангенциальная подстановка
|
tg x = t, |
|
|
|
|
|
x = arctg t, |
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
dt |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
cos2 x = |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
, |
|
sin2 x = 1 |
cos2 x = 1 |
|
|
|
|
|
|
= |
|
|
. |
|||||||||||||||||||||||||||||||||||||||
1 tg2 x |
1 t2 |
|
|
1 t2 |
1 |
t2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Такая подстановка характерна для таких интегралов |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
, |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
, |
|
|
|
tgk x dx. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5sin |
x |
|
|
|
|
x bcos |
x c |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
asin |
|
|
|
|
|
a btg x c tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
tg x = t, |
|
|
|
dx = |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3. |
|
|
|
|
|
|
= |
|
|
|
1 t2 |
|
= |
1 t2 |
|
|
= |
|
|
|
= |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 cos |
x |
|
|
|
cos2 x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
3t |
4 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= 1 |
|
|
|
|
dt |
|
|
|
|
|
1 |
|
|
|
|
|
arctg t |
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|
|
= |
|
3 |
3 |
= |
|
|
|
|
3 |
|
3tg x |
c |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
4/3 |
3 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||

4. dx4 |
|
|
tg x = t |
cos2 x = |
1 |
|
|
|||
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
|
= |
1 t2 |
= |
|||||||
x |
|
|
dt |
|
||||||
cos |
|
dx = |
|
|
|
|
|
|
||
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
= (1 t2 ) dt = t t3 |
|
tg3x |
|
|
|
|
|
|
|
|
= tg x |
|
||||
= |
|
|
1 t2 |
C. |
|||||||
|
|
|
|
|
|
||||||
|
( |
1 |
)2 |
|
3 |
3 |
|
||||
|
|
|
|
|
|||||||
|
|
1 t2 |
|
|
|
|
|
|
|
||

3 x dx, |
|
5 x dx , |
|
|
4 x |
|
|
3 x dx, |
|
|
sin3 x dx, |
cos3 x |
||||||||
sin |
cos |
sin |
|
cos x |
||||||||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin4 x dx, |
||||||
характерной особенностью которых является наличие в числителе |
||||||||||||||||||||
sin x или cos xв |
н е ч е т н о й степени используется прием |
|||||||||||||||||||
|
|
|
|
подведения под знак дифференциала: |
||||||||||||||||
|
|
|
|
cos x dx = d(sin x) |
|
|
sin x dx = d(cos x), |
|||||||||||||
3. |
sin3 x dx = sin2 x(sin x dx) = sin2 x d(cos x) = |
|||||||||||||||||||
= (1 |
|
2 x) d(cos x) = |
(d(cos x) |
cos |
2 x d(cos x)) = |
|||||||||||||||
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
d(cos x) |
|
|
2 |
x d(cos x) = cos x |
|
cos3 x |
C. |
|
||||||||||
|
cos |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Интегрирование тригонометрических функций
В интегралах вида cos2 x dx, sin4 2x dx. |
|
cos2 x sin6 x dx, |
||||||||||
только с четными степенямиsin x, cos x |
|
|
|
|||||||||
применяются |
|
|
формулы |
понижения |
|
|
|
|||||
степени |
|
|
|
1 |
cos 2x |
|
|
|
1 cos 2x . |
|
||
sin2 x = |
, |
cos2 x = |
|
|||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
x |
|
1 |
cos x |
|
1 |
|
cos x |
|
||
1. sin |
|
|
dx = |
2 |
dx = |
|
dx |
|
2 |
dx |
||
|
||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|||
= |
1 |
dx 1 |
cos x dx = |
1 x |
1 sin x C. |
|
||||||
|
2 |
2 |
|
|
2 |
2 |
|
|
|
|
||

5. При решении интегралов применяются некоторые искусственные приемы, например
|
|
5. |
|
|
|
dx |
= |
|
sin2 x cos2 x |
dx |
= |
|
|
|
|
|
|
|||||||||||||
|
|
2 |
xcos x |
|
sin |
2 |
xcos x |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
sin2 x |
|
|
dx |
cos2 x |
|
|
dx = |
dx |
|
|
|
cos x |
dx = |
||||||||||||||||
|
2 |
xcos x |
|
2 |
xcos x |
|
|
|
|
|
2 |
x |
||||||||||||||||||
|
sin |
|
|
|
sin |
|
cos x |
|
|
|
sin |
|
|
|
||||||||||||||||
|
|
|
|
|
dx |
|
|
|
d(sin x) |
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= |
|
|
|
|
|
|
|
|
|
= ln |
tg |
|
|
|
|
|
|
|
|
|
|
|
|
C. |
||||||
cos x |
sin2 x |
|
2 |
|
|
sin x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||||||||

Интегрирование тригонометрических выражений
5) cos2x sin3x dx 12 sin5x sin x dx 101 cos5x cos x C
Формулы преобразования произведения в сумму: sin cos 12 (sin( ) sin( ))
cos cos 12 (cos( ) cos( )) sin sin 12 (cos( ) cos( ))

§3. Интегрирование иррациональных функций.
Дифференциальный бином. Теорема Чебышева.
и решении большинства типов интегралов от иррациональных функций именяется метод замены переменной (или подстановки).
лью замены является избавление от иррациональности.
|
|
|
|
|
x = t4 , dx = 4t3dt |
|
|
t2 |
4t3dt |
t5 dt |
|
|||
|
|
|
|
|
|
|
||||||||
1. 1 4x |
|
|
|
|
||||||||||
|
|
dx = |
1 4 |
|
= 1 t, t4 |
|
|
|
= |
1 t |
= 4 1 t |
= |
||
|
|
x |
x |
|||||||||||
x |
||||||||||||||
= 4 t4
|
|
t |
5 |
|
t |
4 |
|
|
|
|
|
||
= 4 |
5 |
4 |
||||
|
|
|
||||
|
|
|
|
|
|
|
t3
t3
3
t2
t2
2
|
|
1 |
|
|
|
|
5 |
|
|
t 1 |
|
|
|
|
|
dt = (здесь выполнено делениеt |
|
на |
|
1 |
|
|
|
||||||
|
|
t |
(1 t) ) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
t ln |1 |
|
|
|
|
|||||
t | = |
|
x |
|
||||||
|
|
|
|
|
|
(возвращаемся к переменной ) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
x |
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|||||||
= 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
x |
ln |1 |
4 |
x |
| |
c |
||||
|
5 |
|
|
4 |
|
3 |
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

2. |
x2 |
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) Применим подстановку |
|
|
|
|
= t |
|
|
|
|
|
||||||||||
|
|
|
x 7 |
|
|
|
|
|
||||||||||||
2) Найдем |
x 7 = t |
2 |
, x = t |
2 |
7, |
dx = (t |
2 |
|
||||||||||||
|
|
|
7) dt = 2t dt |
|||||||||||||||||
3) Подставим в исходный интеграл и проинтегрируем |
||||||||||||||||||||
= |
(t2 7)2 |
t 2t dt = 2 t2 (t2 |
7)2 dt = 2 t2 |
(t4 |
14t2 49) dt = |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= 2 (t6 |
|
|
|
|
|
|
|
7 |
14 t |
5 |
49 t |
3 |
|
|
|
|
|||
|
14t4 49t2 ) dt = 2 t |
|
|
|
|
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
7 |
|
5 |
3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4)Возвращаемся к старой переменнойx
спомощью обратной замены: t = 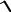
 x 7
x 7
x2 |
|
dx = 2 |
|
28 |
|
98 |
|
C. |
|
(x 7)7 |
(x 7)5 |
(x 7)3 |
|||||
x 7 |
||||||||
|
7 |
5 |
3 |
|
|
|||
|
|
|
||||||
