Для нахождения ординат нижней и верхней точек области решаем систем
x y2 = 12, |
x = 12 y2 |
, |
|
12 y2 = 4 y, |
|
y1= 2, |
|
|
|
y2 4 y 12 = 0, |
y2 = 6. |
||
x 4 y = 0, |
x = 4 y, |
|
|
|
||
Итак, проекцией области на ось |
OYбудет отрезок [ 2; 6]. |
|||||
аким образом, для расстановки пределов интегрирования в повторном |
|||||||||
нтеграле мы имеем: при изменении переменнойy в интервале [ 2; 6]. |
|||||||||
|
x |
|
|
|
|
|
|
|
|
значения переменной будут находиться в пределахот x1( y) = 4 y |
|||||||||
(линия входа в область) до |
|
|
|
2 |
(линия |
|
|
|
|
|
x2 ( y) = 12 y |
|
выхода). |
12 y2 |
|
||||
апишем повторный |
|
d |
x ( y) |
|
|
6 |
|
||
f (x, y)dx dy = |
dy |
2 |
f (x, y) dx = |
dy |
|
f (x, y) dx. |
|||
интеграл |
|
|
|
|
|
|
|
||
|
(D) |
c |
x1( y) |
|
|
2 |
4 y |
|
|
Вычисление двойного интеграла в декартовой системе координат
Вычислить интеграл от функцииz = ограниченной указанными линиями.
z f (x, y) = x y, (D) : 2x 3y 6 = 0, 2x 3y 2 = 0,
y = 2, y = 3.
f (x, y) по области (D) , 1) Строим область
2) При построении повторного интеграла внутреннее интегрирование целесообразно проводить по переменной
x, а внешнее -- по y
|
|
d |
x2 ( y) |
|
(x, y) dx dy = |
|
|
f (x, y) dx |
|
f |
dy |
|
( D2 ) |
c x1( y) |
3) Для расстановки пределов заметим, что переменнаяy
y = 2(ордината крайней нижней границы) доy = крайней верхней границы).
Внутренняя переменнаяx при этом меняется отx1(
(на входе )-- левой границе области до 3
x2 ( y) = 2 y 1
изменяется от 3 ( ордината
y) = 32 y 3
(на выходе) -- правой границе.
Эти пределы мы получили, выражая переменнуюxиз уравнений прямых.
4) Записываем интеграл в виде повторного и вычисляем его
|
|
|
3 |
|
3 y 1 |
|
3 |
|
(x y)2 |
3 y 1 |
|
||
|
|
|
|
2 |
|
|
|||||||
(x y) dx dy = dy (x y) dx dy |
|
|32 y 3 |
|
= |
|||||||||
2 |
|||||||||||||
( D) |
|
|
2 |
|
3 |
|
2 |
|
2 |
|
|
||
|
|
|
|
|
2 y 3 |
|
|
|
|
|
|
|
|
= 1 |
3 |
3 y 1 y |
2 |
|
3 y 3 y |
|
2 dy = |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
3 |
25 |
y |
2 |
5 y 1 |
25 |
y |
2 |
15y 9 |
|
1 |
3 |
10 y 8 dy = |
|
|
|
|
|
|
dy = |
|
|
||||||
|
2 |
|
4 |
|
|
|
4 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|||||
= |
3 |
|
|
5 |
y |
2 |
|
3 |
5 |
(9 4) 4 (3 2) = |
17 |
= 8,5. |
|
|
|||||||||||
|
5y 4 dy = |
|
|
4 y |
| = |
|
|
|||||
|
|
|
2 |
|
|
|
2 |
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||||
ычисление двойного интеграла можно проводить не только в декартовой, |
|
о и в других криволинейных координатах. Наиболее часто используются |
|
олярные координаты на плоскости. Переходить к полярным координатам |
|
меет смысл в тех случаях, когда область интегрирования представляет |
|
бой круг или его часть, а подынтегральная функция содержит сумму |
|
вадратов переменных |
x2 y2 |
Итак, перейдем к рассмотрению вопроса о замене переменных в двойном интеграле.
Двойной интеграл в полярных
координатах
Полярная система координат включает в себя полюс (точка О) и полярную ось (выходящий из точки О горизонтальный луч ОА) Положение любой точки М на плоскости в полярной системе координат задается двумя числами:
=| OM-- полярный| радиус, равный расстоянию от полюса до точки
--полярный угол, измеряемый в радианах
= AOMв направлении против движения часовой стрелки.
Полярные и декартовы координаты одной и той же точки М связаны равенствами:
|
|
|
|
|
|
|
|
|
|
|
2 |
y |
2 |
, |
|
x = cos , |
= x |
|
|
||||
|
y . |
|
|
||||
y = sin . |
tg = |
|
|
||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||
ть имеется двойной интеграл, записанный в декартовой системе координ
f (x, y) dx dy
( D)
При вычислении двойного интеграла в полярной системе координат следует
придерживаться следующей схемы.
1)Построить область интегрирования.
2)В подынтегральной функцииf (x, y) заменить согласно формулам
замены переменных при переходе к полярным координатам
x = cos , y = sin .
Тогда f (x; y) = f ( cos , sin ).
3) Записать элемент площадивполярной системе координат
ds = dxdy d d
4)Уравнения линий, ограничивающих областьD* записываются
вполярных координатах
Таким образом, получим двойной интеграл, записанный в полярной системе координат
f (x, y) dxdy = f ( cos , sin ) d d
(D) |
(D*) |
|
|
Этот интеграл необходимо свести к повторному. Для этого |
|||
|
|
и |
|
5) Определяются пределы изменения переменных |
|
||
и строится соответствующий повторный интеграл. |
|
|
|
При этом следует иметь ввиду, что уравнения линий в |
|||
полярных координатах, как правило, имеют вид |
|
||
, |
= ( ) |
|
|
|
|
|
|
поэтому внутренний интеграл практически всегда вычисляется |
|
по переменной |
, а внешний -- по |
В полярной системе координат при расстановке пределов интегрирования удобно использовать стрелку, пересекающую область. Такой стрелкой является луч, выходящий из полюса и пересекающий границы области на линии входа и выхода.
Подавляющее большинство областей интегрирования в полярной системе координат можно соотнести с одной из 4-х приведенных схем, где для каждого случая записаны соответствующие повторные интеграл
Полюс внутри или на границе области интегрирования
2 |
( ) |
2 |
( ) |
d f ( cos , sin ) d |
d f ( cos , sin ) d |
||
0 |
0 |
1 |
0 |
|
Полюс вне области интегрирования |
||
2 |
2 ( ) |
2 |
2 ( ) |
||
d |
f ( cos , sin ) d |
d |
f ( cos , sin ) d |
||
0 |
|
1( ) |
1 |
|
1( ) |
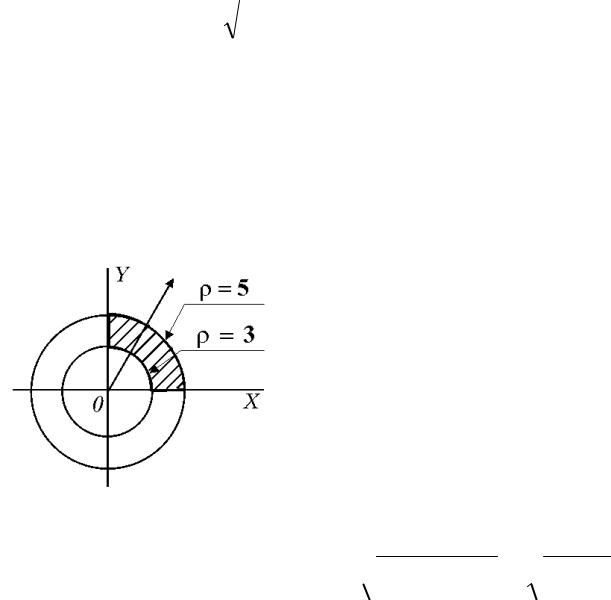
1. Вычислить интеграл, перейдя к полярным координатам
|
|
|
|
|
|
x2 y2 |
9 dxdy |
|
|
||
(D) |
|
|
|
|
|
по области (D) :{x2 y2 |
9, x2 y2 25, |
x 0, |
y 0}. |
||
1) Построим область.Она. представляет собой кольцо, образованное двумя окружностями с центром в начале координат и радиусами 3 и 5
Условия x 0, y 0
означают, что из кольца остается только часть, лежащая в I-ой четверти.
Подынтегральная функция содержит сумму |
||||
квадратов x |
2 |
y |
2 |
поэтому имеет смысл |
|
|
, |
||
перейти в исходном интеграле к полярным координатам.
2)Элемент площади ds = dx dy = d d .
3)Подынтегральная функция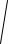
x2 y2 9 = 
2 9.
4) Уравнение границы области также записываем в полярной системе координат
x2 y2 = 9 2 = 9 = 3.
x2 y2 = 25 z 2 = 25 = 5.
Переменная изменяется в пределах от0 до /2.
Так как в данном примере полюс полярной системы координат- вне области интегрирования, то переменная внутреннего интеграла
изменяется в пределах от 1 = 3 (линия входа луча в область)
до |
|
2 |
= 5 |
|
|
|
|
|
|
|
|
|
(линия выхода луча из области). |
|
|
|
|
|
|||||
|
|
|
5) Строим повторный интеграл |
||||||||
|
|
|
|
|
|
|
/2 |
5 |
|
|
|
|
|
|
|
x2 |
y2 9 dxdy = |
2 |
9 d = |
||||
|
|
|
|
d |
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(D) |
|
|
|
0 |
3 |
|
|
|
Так как пределы внутреннего и внешнего интегралов постоянные, то можно вычислить внешний и внутренний интегралы независимо друг от друга и результаты перемножить.
|
/2 |
|
|
|
|
5 |
|
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
||
|
|
|
2 |
|
/2 |
|
2 |
|
|
2 |
||||||||||||
= |
|
d |
|
|
|
|
9 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
d = |0 |
|
2 |
|
|
9 d( |
9) = |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
= 1 |
2 ( 2 |
9)3/2 |5 |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
2 |
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|||||
|
|
[ (25 9)3/2 (9 9)3/2 |
] = |
|
163/2 |
= |
. |
|||||||||||||||
|
6 |
|
||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|