Добавил:

PickyEater13 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

Высшая математика

Файл:

Математика / Комплексные числа и функции.ppt

Скачиваний:

Добавлен:

27.11.2024

Размер:

838.14 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 44

Дифференцирование функций

Пусть функция w = f (z)	определена в	z	0
	точке		0

инекоторой ее окрестности.

Оп р е д е л е н и е. Производной функции в точкеz0 называется

конечный предел отношения приращения функции к приращению

аргумента при стремлении последнего к нулю

	\|z			d	f (z0 ) = lim z 0	f (z0 )	,

w		0	= f (z0 ) =	dz		z

Правила и формулы дифференцирования те же, что и для функции.

действительного переменного.
									z 2									1	1
			2										3
			2										3
	1. z			4z 5 =
	1. z			4z 5 =					z2 4z 5 .		2.	(ln				z )	=	3	z .
					1									2						2
	3.	tg e2 z			=				e2 z 2.		4.	e z			=		2z e z				.
	3.	tg e2 z			=	cos2 e2 z			e2 z 2.		4.	e z			=		2z e z				.
	5.	arcctg z3 =						1		3z2 .
	5.	arcctg z3 =						6		3z2 .
							1 z

Таблица производных

1. zk

= k zk 1

10.

(tg z)' =

cos2 z

' =

11. (ctg z)' =

sin2 z

12.

(arcsin z)

4. az

= az ln a

13.

(arccos z)'

1 z2

= ez

14.

(arctg z)' =

1 z2

loga z '

15.

(arcctg z)'

z ln a

1 z2

ln z

' =

16.

(sh z)' = ch z

(ch z)' = sh z

8. (sin z)' = cos z

17.

(cos z)'

= sin z

18.

(th z)' =

ch2 z

п р е д е л е н и е. Однозначная функция называется аналитической данной точке, если она дифференцируема в этой точке и ее окрестности.

ункция, дифференцируемая во всех точках некоторой области, азывается аналитической в этой области.

Геометрический смысл производной

Пусть аналитическая функция w = f (z)множество точек из области определения функции z = x iyна множество точек плоскости

w = u iv .	f (z0 ) = lim z 0	w	,
Если в точке z0существует производная
		z

то модуль производной функции в точкеесть коэффициент растяженияk плоскости z = x iy в точке z0при данном отображении

| f (z0 ) |= k.

Аргумент производной функцииесть угол поворота плоскости z = x iy в точке z = z0 при данном отображении

arg f (z0 ) =

адача. Найти коэффициент растяжения и угол поворота комплексной
лоскости	z = x iy в точке z0	при отображении w = f (z).
1. f (z) = z2 (1 i)z,		z0 = 1 i.

Находим производную функции

w = 2z (1 i)

Вычисляем значение производной в точке z0 = 1 2i

w'(z0 ) 2(1 2i) 1 i = 3 3i

Получили комплексное число. Находим его модуль и аргумент и определяем коэффициент растяжения и угол поворота

k=| 3 3i |= 32 32 = 3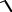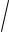2 4,24.

= arg(3 3i) = /4.

Отметим, что значениюk 1соответствует растяжение комплексной плоскости в точке, а значению k 1 -- сжатие.

Интегрирование функций

Пусть функция w = f (z) определена в	z0	и	некоторой	ее
точке		окрестности.

Рассмотрим интеграл f(z)dz

(L)

Re z Im z dz,где L ломаная 0; 1; 1 2i

поэтом Re z Im z dz (x y)d(x iy)

Re z Im z x y

Разбиваем контур интегрирования на два участка:

На отрезке

L1 (z 0; z 1) имеем

y 0,

dy 0,

0 x 1

(x y)d x iy

xdx

( L1 )

На отрезке

(z 1;

z 1 2i)

имеем x 1,

dx 0,

0 y 2

(x y)d x iy

i 2 (1 y)dy i(y

)

i(2 2) 4i

(L2 )

В итоге

Re z Im z)dz 1 4i

(L)

dz	,где L:	z	1,Im z 0
dz	,где L:	z	1,Im z 0
L z
L z

Воспользуемся показательной формой представления функции.

e i / 2

iei d

1,dz iei d , 0

На контуре (L) имеем:

1 e i / 2iei d ei / 2id 2 ei / 2 d i 2ei / 2

2e0

2e i / 2

2 2cos

isin

2 i

Вычислить, используя интегральную формулу Коши:

1) L:

Т.о.

дынтегральная функция имеет 2 особые точки: z=3 и z=2 Эти точки не попадают внутрь контура интегрирования

2)				z 3
		z	2	5z 6
	z 1 1,5	z		5z 6

Подынтегральная функция имеет 2 особые точки (в данном случае точки разрыва):

z1 2,	z2 3 , но только		z1 2

находится внутри рассматриваемого контура интегрирования. Таким образом, в

качестве аналитической функции здесь выступает z 3 f2 z z 3

и по формуле	f z	dz 2 i f z0 имеем
	Г z z0	dz 2 i f z0 имеем

	z	2	z 3	2 i z 3	2 i 2 3	10 i
z 1 1,5	z		5z 6	z 3 z 2	2 3

3)	z 3
	z 4 z2 5z 6	0

В данном случае внутрь контура интегрирования попадают все особые точки.

По одной точке	z1 2 интеграл уже вычислен. В точке			z2 3
решение аналогично предыдущему случаю, только теперь в качестве
аналитической функции будет выступать функция				z 3
и по формуле	f z	dz 2 i f z0	f3	z z 2
	Г z z0
пол
	z 3	z 3	3 3
учим
	z 4 z2 5z 6	2 i z 2 z 3	2 i 3 2 12 i

Окружим каждую точку контурами и представим интеграл в виде суммы двух интегралов, каждый из которых уже вычислен:

	z	2	z 3	f2 z dz f3 z dz 10 i 12 i 2 i
z 4	z		5z 6	z 4	z 4

<<< < Предыдущая 1 2 34 / 44

Соседние файлы в папке Математика

#
27.11.2024539.76 Кб6ДИ-2 предел функции-22.pptx
#
27.11.2024585.64 Кб3ДИ-3 непрерывность функции-22.pptx
#
27.11.2024527.72 Кб3ДИ-4-производная-22.pptx
#
27.11.2024845.46 Кб4ДИ-5-Осн теоремы-22.pptx
#
27.11.20241.53 Mб4ДИ-6-Прилож производных-22.pptx
#
27.11.2024838.14 Кб3Комплексные числа и функции.ppt
#
27.11.2024188.43 Кб3Кратные инт-практика.pptx
#
27.11.20241.08 Mб4Кратные интегралы 2-3.ppt
#
27.11.2024995.84 Кб3Кратные интегралы 4.ppt
#
27.11.2024954.37 Кб4Кратные интегралы-14-ВК.ppt
#
27.11.2024100.35 Кб7Криволинейный и поверхностный интегралы, элементы теории поля, таблица формул.DOC

Дифференцирование функций

Таблица производных

адача. Найти коэффициент растяжения и угол поворота комплексной

Интегрирование функций

Вычислить, используя интегральную формулу Коши: