Аналитическая геометрия в пространстве
ПоверхностиПреподаватель:
Филипенко Николай Максимович
доцент ОМИ ШБИП ТПУ
Раздел «Аналитическая геометрия в пространстве» курса «Линейная алгебра и аналитическая геометрия» включает две основные темы:
1.Плоскость и прямая в пространстве
2.Поверхности 2-го порядка
Глава II. Поверхности 2-го порядка
Общее уравнение плоскости или прямой в пространстве
– есть уравнения линейные относительно переменныхx,y z
и
Уравнение поверхности 2-го порядка
Ax2 By2 Cz2 Dx Ey Fz G 0
Ax2 By2 Cz2 квадратичная часть
Dx Ey Fz G линейная часть
поверхностям . 2-го порядка относятся :
ера, эллипсоид, гиперболоиды, конусы, параболоиды и цилиндры
новная задача состоит в умении по уравнению определить тип верхности, привести само уравнение к каноническому виду и строить поверхность в системе координат.
§2. Центральные поверхности. 1.Сфера
Определение. Сферой называется множество точек пространства, равноудаленных от одной точки, называемой центром
Уравнение сферы с центром в начале координат
x2 y2 z2 R2
Уравнение сферы со смещенным центром O' (x0 ; y0 ; z0 )
(x x0 )2 ( y y0 )2 (z z0 )2 R2
В!уравнение сферы входят квадраты трех переменных, причем коэффициенты при квадратах и знаки при них одинаковые.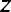 
Построение сферы
Построить сферуx2 y2 z2 6 y
ное уравнение определяет сферу, так как |
|
|||||
ются квадраты всех переменных, знаки и коэффициенты при кото |
||||||
наковые. |
|
|
|
|
|
|
построения сферы необходимо знать координаты центра и радиу |
||||||
ичие слагаемого с первой степенью переменной y указывает на |
||||||
ичие смещения центра сферы по оси OY |
|
|||||
ля приведения уравнения к каноническому виду |
||||||
(x x ) |
2 ( y y |
)2 (z z |
)2 |
R2 |
|
|
0 |
0 |
0 |
|
|
|
|
необходимо выполнить преобразования, |
3 |
|||||
связанные с выделением полного квадрата |
||||||
|
||||||
x2 y2 6 y z2 0 |
|
|
|
|||
x2 ( y2 6 y 9) 9 z2 0 |
|
|
|
|||
x2 |
( y 3)2 |
z2 9 |
|
O' (0;3;0) |
- центр сферы |
|
|
|
|
|
R 3 |
- радиус сферы |
|
Построение сферы
2. Построить сферуx2 y2 z2 2 y 9z 1
е уравнение определяет сферу, так как тся квадраты всех переменных, знаки и коэффициенты при которы ковые.
ичие слагаемых с первой степенью переменных z и y указывает на чие смещения центра сферы по осям OY и OZ
ля приведения уравнения к каноническому виду
(x x )2 ( y y |
)2 (z z |
)2 R2 |
|
|
||||
|
0 |
0 |
|
|
0 |
|
|
|
еобходимо выполнить преобразования, |
|
|||||||
вязанные с выделением полного квадрата |
4,5 |
|||||||
x2 ( y2 2 y 1) 1 (z2 |
9z 4,52 ) |
4,52 1 |
|
|||||
x2 |
( y 1)2 |
(z |
4,5) |
2 |
1 4,52 1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
x2 |
( y 1)2 |
(z |
4,5) |
2 |
22,25 |
O' (0;1;4,5) - центр сферы |
||
R 
22,25- радиус сферы
2. Эллипсоид
Каноническое уравнение трехосного эллипсоида имеет |
||||||||||||||||
вид |
|
x2 |
|
|
y2 |
|
z2 |
1 |
|
|
|
|||||
|
|
|
a2 |
b2 |
c2 |
|
|
c |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, |
b, |
c |
|
|
полуоси |
|
|
|||||||||
|
|
|
|
|
||||||||||||
|
эллипсоида. |
b |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
Центр этого эллипсоида находится |
|
a |
||||||||||||||
|
|
|||||||||||||||
|
|
|
||||||||||||||
в начале координат. |
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение эллипсоида с центром в точкеO' (x0 ; y0 ; z0 ) |
имеет вид |
|||||||||||||||
|
(x x |
)2 |
|
|
( y y |
)2 |
|
(z z |
)2 |
1 |
|
|||||
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
||||
|
|
a2 |
|
|
b2 |
|
|
c2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Признаки уравнения эллипсоида:
1. Наличие квадратов всех трех переменных
2. Одинаковые знаки при квадратах переменных
3. Разные коэффициенты при квадратах переменных
|
Построить поверхностьx2 16y2 4z2 8z 5 |
авнении есть квадраты переменных, знаки при которых одинаковы эффициенты разные. Это эллипсоид, причем со смещенным центр внение нужно привести к каноническому виду
(x a2x0 )2 ( y b2y0 )2 (z c2z0 )2 1 x2 16y2 4z2 8z 5
x2 16y2 4(z2 2z) 5
x2 16y2 4(z2 2z 1 1) 5
x2 16y2 4(z 1)2 4 5
x2 16y2 4(z 1)2 9
x2 |
|
|
16y2 |
4(z 1)2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
|
9 |
|
|
|
9 |
||||||
|
|
|
|
|
|
|
|
|||||
|
x2 |
|
|
|
y2 |
|
|
|
(z 1)2 |
1 |
||
|
9 |
|
9 /16 |
|
9 / 4 |
|||||||
|
|
|
|
|
|
|||||||
3
O' (0;0;1-) центр эллипсоида
Полуоси эллипсоида
a 3, b 3/ 4, c 3/ 2
3. Гиперболоиды
Канонические уравнения гиперболоидов
|
x2 |
|
y2 |
|
z2 |
1 |
|
|
a2 |
b2 |
c2 |
|
|||
|
|
|
|
|
|||
В зависимости от знака перед единицей в |
|
||||||
правой части гиперболоиды делятся на |
|
||||||
одно и двуполостные. |
|
|
|
|
|
||
Каноническое уравнение однополостного |
b |
||||||
гиперболоида |
|
|
|
|
a |
||
|
x2 |
|
y2 |
|
z2 |
1 |
|
a2 |
b2 |
c2 |
|||
|
|
|
|
|||
a, b, |
c |
полуоси |
||||
Признаки уравнения однополостного гиперболоида: личие квадратов всех трех переменных зные знаки при квадратах переменных
дин знак минус при квадрате переменной в левой части уравнения, авой части плюс 1.
Разные ориентации однополостных гиперболоидов
Ориентация гиперболоида зависит от того, перед какой |
|||||||||||||
переменной в каноническом уравнении стоит знак |
|||||||||||||
минус. |
|
|
|
|
Однополостный гиперболоид |
||||||||
Однополостный гиперболоид |
|||||||||||||
с осью симметрии OY |
с осью симметрии OX |
||||||||||||
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|||
|
x2 |
|
y2 |
|
z2 |
1 |
|
x |
|
y |
|
z |
1 |
|
2 |
2 |
2 |
||||||||||
|
|
b2 |
|
||||||||||
|
a2 |
|
c2 |
|
a |
|
b |
|
c |
||||
c