Построить поверхности

1)3z 6 y2 y2 6 3z

y2 3(z 2)

ь цилиндра – OX,

правляющей является парабола сью симметрии OZ , смещенной

2 единицы вверх по оси OZ вершиной ветвями, направленными вниз, ршина O' (0;0;2)

2) y 5 x2

x2 y 5

Ось цилиндра – OZ, направляющей является парабола с осью симметрии' OY, вершинойO (0;5;в0)точке

и ветвями, направленными вправо

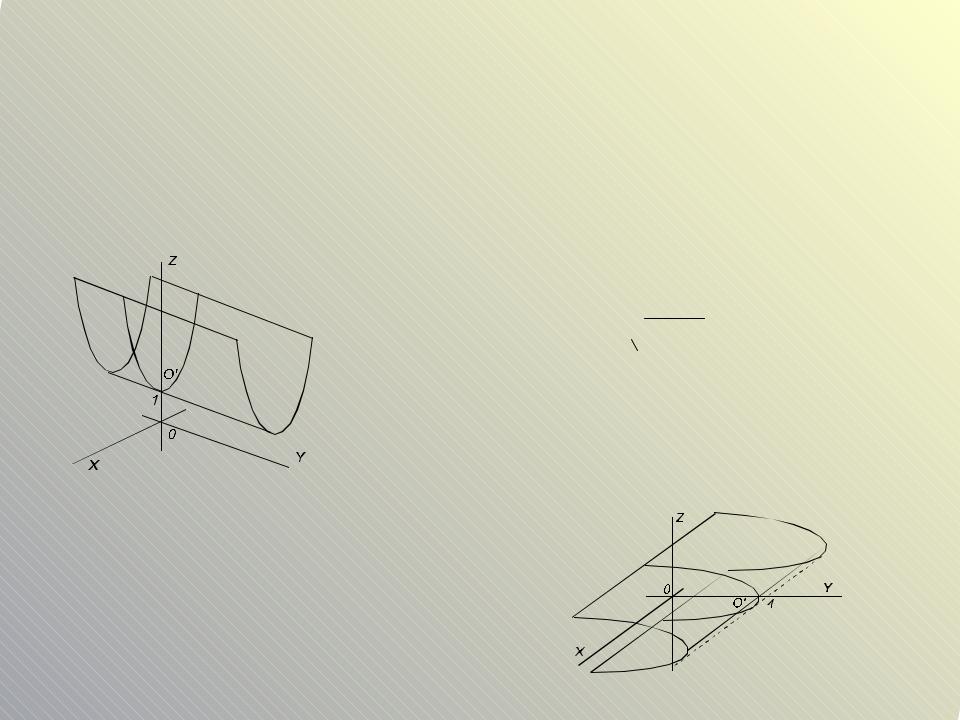
Построить поверхности

4)z 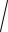4 y, z2 4 y

z2 ( y 4),

сь цилиндра – OX, направляющей является арабола с осью симметрии OY, вершиной точке O' (0;4;0)

ветвями, направленными влево

z 0

Верхняя

половинка