Различные ориентации эллиптических параболоидов
Характерным признаком уравнения эллиптического параболоида является присутствие всех трех переменных, но одно из них входит в уравнение только в первой степени, т.е. в уравнении параболоида отсутствует квадрат одной переменной. Ось симметрии параболоида параллельна той оси, координата которой в yура2 внz2 ении только в первой степени.
b2 c2 2 pxпараболоид с осью симметрии OX
x2 z2 2 pyпараболоид с осью симметрии OY
a2 c2
озможна также смена направления чаши параболоида.
ли в каноническом уравнении в правой части стоит знак минус, параболоид направлен в отрицательном направлении оси симмет
Можно записать один из видов параболоидов со смещенной верши
x |
2 |
2 |
|
|
|
|
|
y |
2 p(z z0 ), |
гдеO' (0;0; z-0 )вершина параболоид |
|
a |
2 |
2 |
|||
|
|
b |
|
|
|
Для построения эллиптического параболоида нужно знать:
1. |
Координаты вершины |
|
|
|||
2. |
Ось симметрии (определяется по переменной, |
|||||
3. |
квадрата которой нет в уравнении) |
|||||
Направление чаши параболоида (определяется по |
||||||
|
знаку |
|
|
|
|
|
|
переменной в правой части канонического |
|||||
• Построить поверхностьx |
2 |
z |
2 |
y 2 |
||
|
уравнения) |
|
|
|||
|
|
|
|
|
||
Уравнение определяет круговой параболоид с осью симметрии OY |
||||||
и смещенной также по оси OY вершиной |
||||||
Приведем уравнение к каноническому виду |
||||||
|
x2 z2 |
2 y |
|
|
|
|
x2 z2 |
( y 2) |
|
|
|
|
|
O' (0;2;0-)вершина параболоида
аша параболоида направлена влево, т.е. в отрицательном аправлении оси симметрии
Построить поверхность |
2x |
2 |
5y |
2 |
3z 1 |
|
|
авнение определяет эллиптический параболоид (так как |
|||||
ффициенты при квадратах переменных различные) с осью симме |
|||||
к как отсутствует квадрат переменной z) и смещенной также |
|||||
оси OZ вершиной |
|
|
|
||
Проведем необходимые преобразования уравнения |
|||||
к каноническому виду x2 |
|
y2 |
2 p(z z0 ), |
||
|
|
a2 |
b2 |
||
|
|
|
|
||
2x2 5y2 1 3z |
|
|
|
||
2x2 5y2 3(z 1/ 3) |
|
|
|||
' |
) |
|
|
|
|
O |
(0;0;1/ 3- вершина параболоида |
||||
Чаша параболоида направлена вниз, т.е. в отрицательном направлении оси симметрии
Замечание: наличие коэффициентов при квадратах переменных при таком схематичном построении можно не принимать во внимание.
Гиперболический параболоид
Каноническое уравнение гиперболического параболоида имеет вид
|
x2 |
|
y2 |
2 pz |
|
a2 |
b2 |
||||
|
|
|
личительным признаком уравнения гиперболического параболоид ляется то что в левой части уравнения между квадратами ременных знак минус. 
аки уравнения гиперболического параболоида: утствие квадрата одной из переменных ные знаки при квадратах переменных в левой ти уравнения
Эта поверхность имеет форму седла.
Возможны различные варианты ориентации гиперболического параболоида в зависимости от оси симметрии, знаков при квадратах.
Цилиндрические поверхности
Цилиндрическая поверхность-это поверхность, которую описывает прямая линия (образующая), которая оставаясь параллельно самой себе движется вдоль некоторой кривой, называемой направляющей. По названию направляющей получают свое название и цилиндры.
Если образующая параллельна какой-либо оси координат, то каноническое уравнение цилиндра не содержит в уравнении соответствующую переменную. В этом случае уравнение цилиндра повторяет уравнение своей направляющей. Вариантов различных уравнений цилиндров достаточно много.
Для построения цилиндра нужно построить направляющую в той плоскости, в которой она задана, а затем «тянуть» эту линию вдоль той оси, Признакикоординатауравнениякоторойцилиндрическойотсутствует в уравнповерхности:нии.
В уравнении цилиндрической поверхности отсутствует одна переменная.
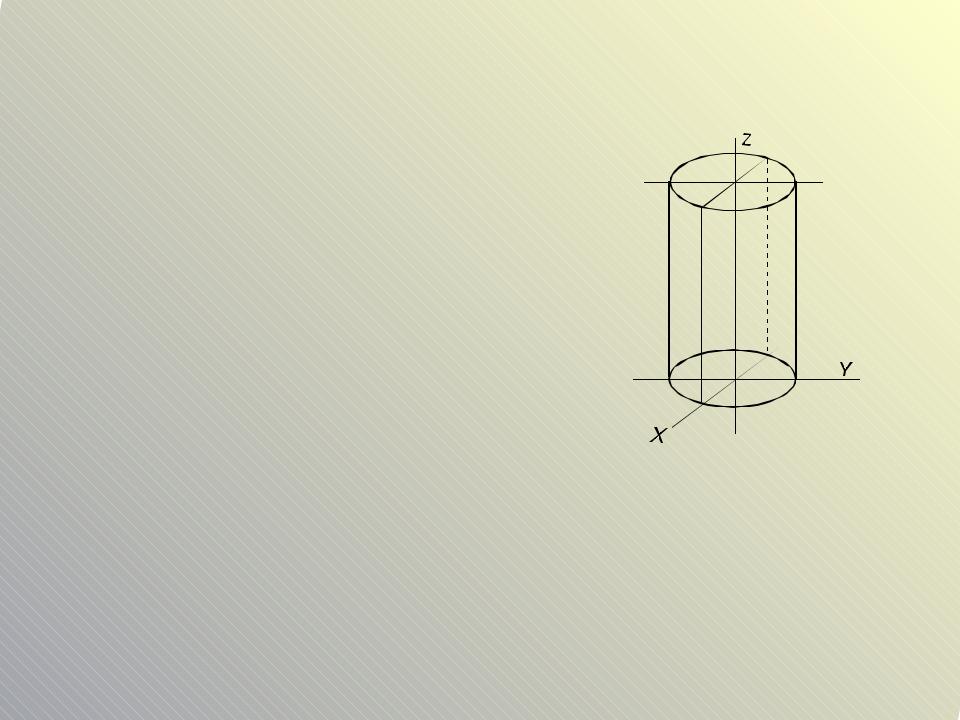
Виды цилиндров
Круговые цилиндры:
Направляющей линией является окружность. x2 y2 R2 ось симметрии OZ
y2 z2 R2 ось симметрии OX x2 z2 R2 ось симметрии OY
рисунке изображен цилиндр с осью симметрии OZ. |
R |
R |
|
построения цилиндра строим окружность радиуса R в плоскости XO ем «превращаем» эту окружность в цилиндр, вытягивая ь оси симметрии.
но построить цилиндр и таким способом: нарисовать две или неско аковых окружностей параллельных друг другу на разной высоте, ем соединить их образующими параллельными оси симметрии.
Эллиптические цилиндры
Направляющей кривой являются эллипсы
x2 |
|
y2 |
|
1 ось симметрии OZ |
|
|
|||||||
a2 |
b2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|||
y |
|
|
z |
|
1 |
ось симметрии OX |
|
|
|||||
2 |
|
2 |
|
|
|
||||||||
b |
|
|
c |
|
|
|
|
|
|||||
x2 |
|
|
|
z2 |
|
1 |
ось симметрии OY |
|
b |
||||
a2 |
c2 |
|
a |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строения цилиндра строим эллипс с полуосями a и b в плоскости м «превращаем» этот эллипс в цилиндр, вытягивая вдоль оси симм
нешнему виду при схематическом построении эллиптический и кру ндры выглядят одинаково.
|
|
|
|
|
Построить поверхности |
|
|
|
|||
x2 z2 2z |
|
y |
2x x2 |
|
|||||||
уравнении отсутствует переменнаяВy.уравнении отсутствует |
|||||||||||
о круговой цилиндр с осью |
переменная z. |
|
|
|
|||||||
мметрии OY. Приводим уравнение |
Это круговой цилиндр с осью |
||||||||||
аноническому виду |
симметрии OZ. |
|
к |
||||||||
x2 z2 |
2z 0 |
Приводим2 |
уравнение2 |
||||||||
x2 z2 |
2z 1 1 0 |
y |
2x |
x |
|
|
|||||
каноническому2 2 |
виду |
|
|
||||||||
x2 (z 1)2 1 0 |
x y 2x |
|
|
||||||||
x |
2 |
(z |
1) |
2 |
1 |
(x 1)2 y2 1, |
y 0 |
||||
|
|
|
|
|
|
|
|
||||
O' (0;0;1) |
R 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Правая |
||
|
|
|
|
|
|
|
|
|
половинка |
||
|
|
|
|
|
|
|
|
|
цилиндра |
||
Гиперболические цилиндры
Вкачестве направляющей этих цилиндров служит гипербола.
|
x2 |
|
|
y2 |
1 ось симметрии OZ |
|
x2 |
y2 |
1 |
||
a2 |
|
|
b2 |
|
|
a2 |
b2 |
|
|||
y2 |
|
|
z2 |
|
1 ось симметрии OX |
|
|
|
|
||
b2 |
|
|
c2 |
|
|
|
|
|
|
||
x2 |
|
|
z2 |
1 ось симметрии OY |
|
|
|
|
|||
a |
2 |
|
c |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
построении гиперболических цилиндров обязательно нужно вильно определить мнимую и действительную оси гиперболы и ось метрии самого цилиндра.
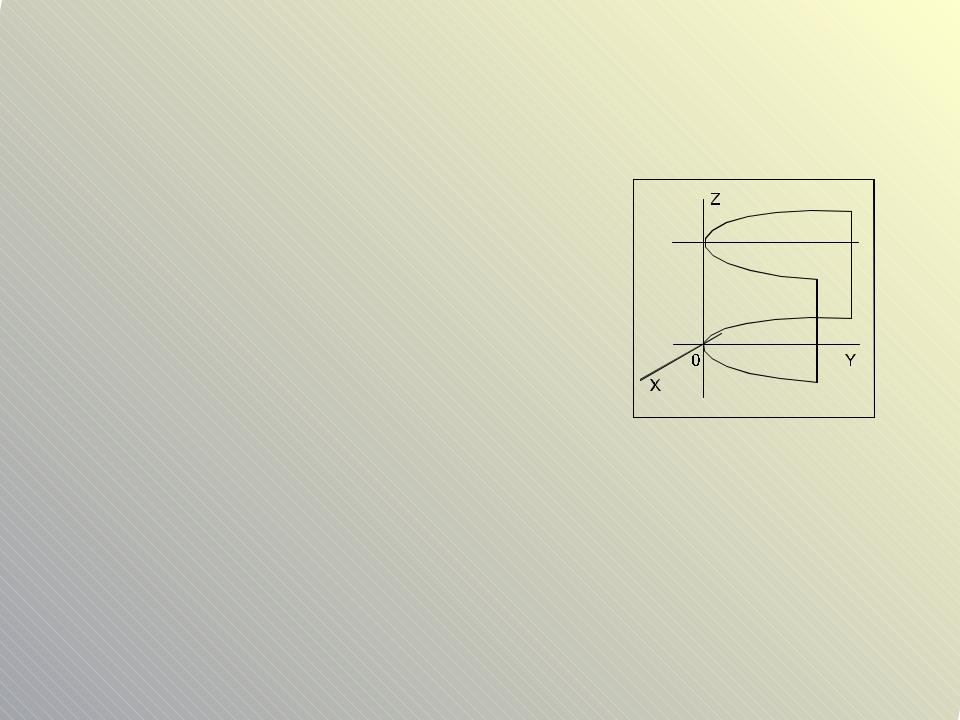
Параболические цилиндры |
|
Направляющей этих цилиндров является парабола. |
|
x2 |
x2 2 py |
2 py |
|
|
ось симметрии OZ |
y2 |
2 px ось симметрии OZ |
y2 |
2 pz ось симметрии OX |
z2 |
2 py ось симметрии OX |
x2 |
2 pz ось симметрии OY |
z2 |
2 px ось симметрии OY |
построении цилиндра нужно определить основные параметры пар |
|
динаты вершины, ось симметрии и направление ветвей, построить |
|
болу, а затем уже строить цилиндр с соответствующей осью симм |
|