Нахождение точки пересечения прямой и
плоскости
Для нахождения точки пересечения прямой и плоскости нужно составить систему из уравнений прямой и плоскости
x x0 |
|
y y0 |
|
z z0 |
t |
|
m |
n |
p |
||||
|
|
|
Ax By Cz D 0
Для того, чтобы решить систему, переводим уравнение прямой в
параметрический вид x mt x0
y nt y0z pt z0
Подставляем эти уравнения в уравнение плоскости
A(mt x0 ) B(nt y0 ) C( pt z0 ) D 0
Из этого уравнения находим параметр t и подставляем его значение в параметрические уравнения , получим координаты точки пересечения
4. Найти точку пересечения и угол между прямой
x 3 |
|
y 5 |
|
|
z 2 |
|
4 |
|
1 |
|
|
||
|
|
3 |
||||
и плоскостью5x 3y 4z 2 0
Для нахождения точки пересечения преобразуем канонические уравнени прямой к параметрическому виду
x 3 |
|
y 5 |
|
|
z 2 |
t, |
|
4 |
|
1 |
|
|
|||
|
|
3 |
|
||||
x 4t 3y t 5
z 3t 2
Подставляем в уравнение плоскости и находим параметр t
5(4t |
3) 3( t 5) 4(3t 2) 2 0 |
|
20t 3t 12t 15 15 8 2 0 |
||
5t 10 |
0, |
t 2 |
Подставляем t в параметрические уравнения
x 8 3 11 |
|
|
Итак, координаты точки пересечения |
y 2 5 7 |
|
|
M ( 11;7; 8) |
z 6 2 8 |
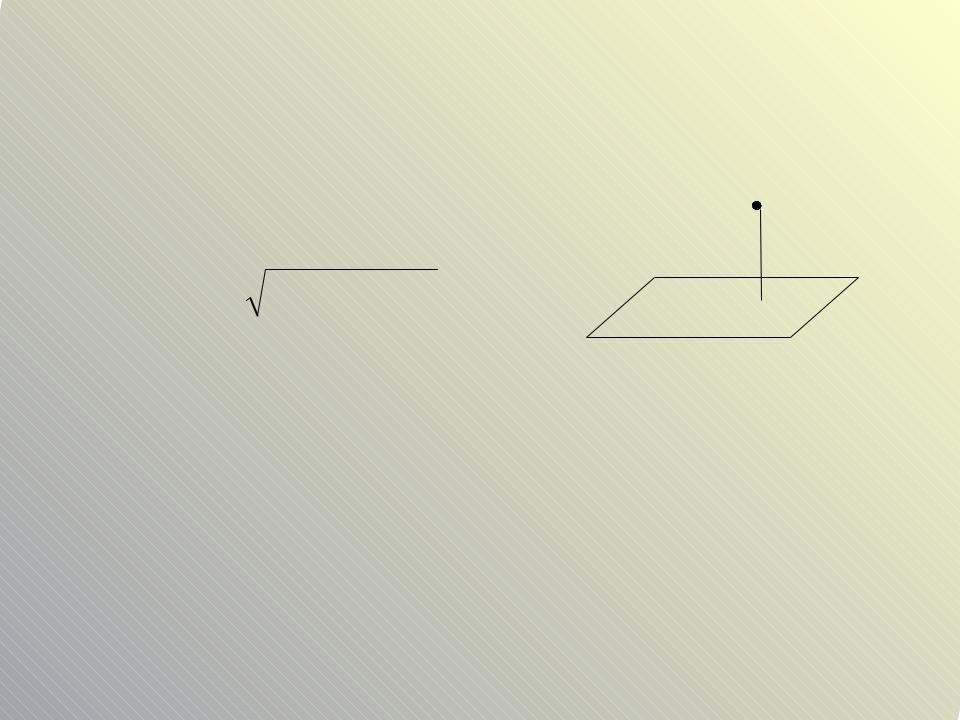
Расстояние от точки до плоскости |
|
|||||
Расстояние от точки1 |
1 |
1 |
1 |
до плоскости |
|
|
|
M |
(x |
; y |
; z ) |
|
|
Ax By Cz D 0 |
|
находится по формуле |
|
|||
| Ax1 By1 Cz1 D | |
|
M1 (x1 |
; y1; z1 ) |
|||
|
d |
|
||||
d |
A2 B2 C 2 |
|
|
|
|
|
|
|
|
|
|
||
тояние – это длина перпендикуляра, опущенного из точки на плос
авило: для нахождения расстояния от точки до плоскости нужно ординаты точки подставить в левую часть уравнения плоскости, зделить на длину вектора нормали плоскости и полученное значен ять по абсолютной величине.
!Расстояние – величина всегда положительная
5. Найти расстояние от точки |
до плоскости |
M (5;3; 2) |
|
3x 4 y z 9 0 |
|
Используем формулу расстояния от точки до плоскости
|
|
|
|
| Ax1 By1 Cz1 D | |
|
|
|
|
|
|
||||||
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C 2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
d |
|
|
3 5 4 3 1 ( 2) 9 |
|
|
|
| 4 | |
|
4 |
|
||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
32 ( 4)2 ( 1)2 |
|
|
|
26 |
26 |
||||||||
Расстояние от точки до прямой в пространстве
Задача о нахождении расстояния от точкиM1 (x1; y1; z1 ) |
|||||||
до прямой |
x x0 |
|
y y0 |
|
z z0 |
|
|
m |
n |
p |
|||||
|
|
|
|||||
шается так же, как в векторной алгебре находилась высота раллелограмма, построенного на двух известных векторах.
M1 |
(x1; y1 |
; z1 ) |
На векторах |
|
|
|
d |
s |
M0 M1 x1 x0 ; y1 y0 ; z1 z0 |
||
и |
s m;n; p строим |
|||
M0 (x0 ; y0 ; z0 ) |
||||
|
параллелограмм. |
|||
Высота этого параллелограмма и есть искомое расстояние.
у находим как отношение площади параллелограмма не основания. Площадь параллелограмма – это модуль векторного ведения векторов, а длина основания – это длина вектораs
d M 0 M1 s s
5. Найти расстояние от точкиM ( 1;4; 2) |
до прямой в |
||||||
пространстве |
x 2 |
|
y 4 |
|
z |
|
|
|
3 |
5 |
1 |
|
|
||
M ( 1;4; 2)
d |
s 3; 5;1 |
|
M0 (2; 4;0)
Искомое расстояние – это высота |
|
параллелограмма, построенного на |
|
векторах |
и M0 M 3;8; 2 |
s 3; 5;1 |
|
Площадь параллелограмма находим, используя векторное произведен
|
|
s M0 M |
|
i |
j |
k |
|||||||
S |
|
|
3 |
5 |
1 |
|
2i 3 j 9k |
|
|
|
|||
|
|
|
|
22 32 92 |
|
|
|
||||||
|
|
|
94 |
||||||||||
|
|
|
|
3 |
8 |
2 |
|||||||
Длина основания – это длина вектораs 3; 5;1
s 
32 ( 5)2 12 
35
Расстояние от точки до прямой d Ss 
9435
Взаимное расположение прямой и плоскости в пространстве
1. Условие параллельности прямой и плоскости
N A; B;C |
s m;n; p |
s |
N |
(N s) 0 |
|
Am Bn Cp 0
. Условие перпендикулярности прямой и плоскости
s m;n; p |
N A; B;C |
|
|
|
|
|
|
|
|
|
N || s |
A |
B |
C |
|
|
|||
|
|
|||
|
|
m |
n |
p |
|
|
Взаимное расположение прямой и плоскости в |
||
|
|
пространстве |
3. Нахождение угла между прямой и плоскостью |
||
N A; B;C |
s m;n; p |
Углом между прямой и плоскостью |
|
считается угол между этой прямой |
|
|
|
и ее ортогональной проекцией на |
|
|
|
|
эту плоскость. На рисунке это угол |
|
|
|
Из уравнений прямой и плоскости |
|
|
известны направляющий вектор |
|
|
прямой и вектор нормали плоскости. |
синус угла |
между этими векторами легко можно найти. |
|
|
|
и в сумме дают 90 градусов, а знач |
гко заметить, что углы |
||
cos sin |
|
|
Поэтому при нахождении угла между прямой и плоскостью |
||||||||||||||||||
находят |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не косинус, а синус угла. Кроме того, в формуле стоит |
||||||||||||||||||
| (N s) | |
|
|
|
| |
Am Bn Cp | |
|
|
|
|
|||||||||
модуль, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin |
|
данно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
синус угла в |
|
й ситуации может быть только |
||||||||||||||||
положительным |
|
N s |
|
|
A |
2 |
B |
2 |
C |
2 |
m |
2 |
n |
2 |
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нахождение точки пересечения прямой и
плоскости
Для нахождения точки пересечения прямой и плоскости нужно составить систему из уравнений прямой и плоскости
x x0 |
|
y y0 |
|
z z0 |
t |
|
m |
n |
p |
||||
|
|
|
Ax By Cz D 0
Для того, чтобы решить систему, переводим уравнение прямой в
параметрический видx mt x0
y nt y0z pt z0
одставляем эти уравнения в уравнение плоскости
A(mt x0 ) B(nt y0 ) C( pt z0 ) D 0
этого уравнения находим параметр t и подставляем его значение араметрические уравнения , получим координаты точки пересечен
Составление уравнений плоскости
Составить уравнение плоскости, проходящей через точку
M0 ( 1;3; 5) a 3; 2;4
перпендикулярно вектору Исходное уравнение:
A(x x0 ) B( y y0 ) C(z z0 ) 0
Подставляем координаты точки и вектора
3(x 1) 2( y 3) 4(z 5) 0
Раскрываем скобки
3x 3 2 y 6 4z 20 0
Приводим подобные
3x 2 y 4z 29 0
Получили общее уравнение плоскости.