Добавил:

PickyEater13 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

Физика общая

Файл:

3 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ НА ТЕМУ ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

.pdf

Скачиваний:

Добавлен:

27.11.2024

Размер:

560.91 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

Q U , т.е. подведенное к газу тепло целиком идет на изменение внутренней энергии газа. Интенсивность теплового движения молекул газа увеличивается, внутренняя энергия газа увеличивается.

Рассмотрим процесс АВ2. это процесс изобарический, т.е. идущий при постоянном давлении p=Const.

Записываем первое начало термодинамики Q U A . При p=Const газ совершает работу A p V , где V - изменение объема газа, но и внутренняя энергия газа тоже увеличивается.

Изменение внутренней энергии газа U	m	i	R T , где ∆Т –	изменение
Изменение внутренней энергии газа U	2		R T , где ∆Т –	изменение
	2
температуры газа. Запишем уравнение Менделеева - Клапейрона				pV	m	RT .
температуры газа. Запишем уравнение Менделеева - Клапейрона				pV		RT .

При процессе АВ2	увеличивается объем, а при увеличении объема V
увеличивается температура Т, следовательно, увеличивается внутренняя
энергия газа.
Рассмотрим процесс АВ3. Это изотермический процесс, т.е. процесс, идущий
при постоянной	температуре, Т=Const. Запишем первое начало

термодинамики Q U A .			Изменение	внутренней	энергии газа
выражается формулой U	m	i	R T , ∆U=0,	так как при	изотермическом
	2

процессе равно нулю изменение температуры, ∆T=0. Тогда ∆Q=∆A, т.е. все количество теплоты, подведенное к газу, идет на совершение газом работы.

Внутренняя энергия газа, выражается формулой U	m	i	R T , остается при
	2

этом постоянной.
Ответ: Процесс АВ1: нет, увеличивается;
Процесс АВ2: да, увеличивается;
Процесс АВ3: да, остается постоянной.

Задача 7

Молярная теплоемкость идеального газа при некотором процессе изменяется по закону C T , где α – постоянная величина.

Найти: а) работу А, совершаемую киломолем газа при его нагревании от температуры Т1 до температуры Т2=2Т1; б) уравнение, связывающие параметры p и V при этом процессе. Коэффициент Пуассона для данного газа равен γ.

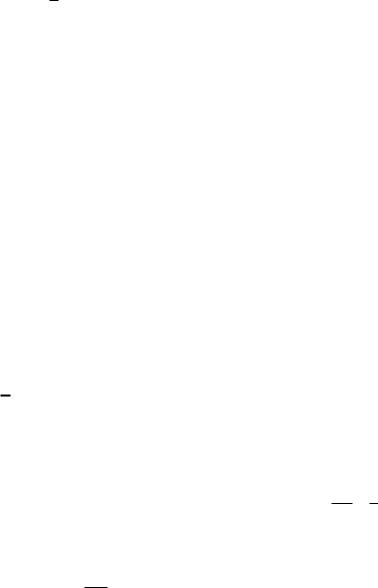
Дано:									Решение:
	m	1кмоль					а)		запишем	первое	начало
		1кмоль					термодинамики в дифференциальной
							термодинамики в дифференциальной
							форме dQ dU dA .
С Т							dQ	-	бесконечно	малое	количество
Const							теплоты, подведенное к данной массе
T2 2T1							газа;
А=?							dU -бесконечно малое изменение
внутренней энергии данной массы газа;
dA - бесконечно малая работа, совершаемая газом при его нагревании.
dA dQ dU , dQ			m	CdT , где	m	1кмоль		по	условию	задачи,	молярная
dA dQ dU , dQ				CdT , где		1кмоль		по	условию	задачи,	молярная

теплоемкость C T , dT – бесконечно малое изменение температуры. Для одного кмоля газа dU 2i RdT , где i – число степеней свободы данного

идеального

газа.

Тогда

dA CdT

RdT

RdT , R –

универсальная

газовая постоянная.

Вся работа А, совершаемая газом при его нагревании от температуры T1 до

температуры Т2, выражается формулой

dT ln

R(T T ) . Учитывая, что Т =2Т

, получим

A ln 2

. Число степеней свободы i в данной задаче не указано, но

коэффициент Пуассона γ дан. Коэффициент Пуассона

i 2

или 1

отсюда

. Тогда работа

A ln 2

RT1

б) запишем первое начало

термодинамики в

дифференциальной

форме

dQ dU dA.

Учитывая,

что

1кмоль по

условию

задачи,

имеем

dQ CdT T dT , dU 2i RdT . Бесконечно малую работу dA при бесконечно

малом изменении объема ∆V газа можно находить по формуле dA pdV , считая, что давлеение газа р не успеет измениться за то бесконечно малое время, в течении которого изменяется объем газа. Теперь, учитывая, что

C T , первое начало термодинамики можно записать так dTT 2i RdT pdV ,

но в этом уравнении три переменные величины T, p и V. Пользуясь уравнением Менделеева-Клапейрона для одного киломоля pV=RT, выражаем

р через переменные Т и V: p RTV . Тогда первое начало термодинамики будет

выглядеть

так

RdT

dV .

Делим на

RT все

члены

уравнения

. Берем

интеграл

от

левой

правой

частей

уравнения

2 T

dV 1

1 i

ln T2

ln T1 ln V2 ln V1

;

R T1 T

2 T1

V R

или

ln T

ln V

ln T

ln V

Как

видно

из

вышесказанного

RT1

RT2

ln T ln V

является

постоянной

величиной.

По

условию задачи,

RT1

требуется найти уравнение, связывающие параметры p и V, поэтому параметр Т надо исключить. Из уравнения Менделеева-Клапейрона pV=RT. Находим

. Тогда

ln V C

, где С

– постоянная величина. Находим

число степеней свободы i. Коэффициент Пуассона

i 2

, отсюда

ln V C

. Так как

логарифм произведения

равен

сумме

логарифмов

сомножителей,

то

ln( pV ) ln V C

. Или

ln( pV )

ln( pV ) ln V C

Выражение C

является постоянной величиной. C

Const

1 R

. Тогда

ln( pV ) ln V Const ,

или

( 1) ln( pV ) ( 1) ln V Const ,

или

( 1)

ln( pV ) ln V 1 Const ,

( 1) ln( pV ) Const .

Потенцируем

( 1)

pV e pV

Const . Получим уравнение, связывающие параметры p и V в

данном процессе, е – основание натурального логарифма.

	RT1		( 1)
Ответ: A ln 2		,	pV e pV
	1

Const .

Задача 8

Один киломоль идеального одноатомного газа расширяется по политропе с показателем n=1,5, причем его температура уменьшается на один градус. Определить:

а) молярную теплоемкость С газа при этом процессе; б) количество тепла ∆Q, полученного газом;

в) работу А, совершаемую газом. За счет, каких источников энергии совершается эта работа?

Дано:

Решение:

1кмоль

а) так как газ одноатомный, то число

степеней свободы для i=3, что можно

n 1,5

вписать в данные задачи. Молярная

T 1K

теплоемкость С идеального

газа в

политропическом

процессе

R 8,3 103 Дж

выражается

формулой

кмоль К

i 3

C R

C= ? А=? Q=?

( 1)(n 1)

где R-универсальная газовая постоянная, n-показатель политропы, γ-

i 2

коэффициент Пуассона. Так как

i 2

, то C R

. Подставим

(

i 2

1)(n 1)

1,5

i=3. C R

0,5R, C 0,5R . Подставляя численное значение

(

1)(1,5 1)

универсальной газовой постоянной R, получим

C 0,5 8,3 103

Дж

4,15 103

Дж

;

кмоль К

кмоль

б) количество теплоты Q, полученное одним киломолем идеального газа,

подсчитывается по формуле Q=C T,

где C-молярная теплоемкость газа.

Так как

C 0,5R ,

то Q 0,5R T .

Подставлим

численные

данные

Q 0,5 8,3 103 ( 1) кмольДж 4,15 103 кмольДж ;

в) запишем первое начало термодинамики Q U A . Отсюда A Q U


Изменение внутренней энергии для одного киломоля газа U		i	R T , так как

	2
i=3, то U 1,5R T . Подставляя U и	Q в формулу для работы, получим
A 0,5R T 1,5R T 2,0R T, A 2,0R T .	Знак «минус» имеет		физический

смысл. Работа совершается за счет поглощения тепла и за счет уменьшения

внутренней		энергии				газа.			Подставим							численные	значения
A 2,0 8,3 103 ( 1)				Дж	16,6 103				Дж	.
A 2,0 8,3 103 ( 1)					16,6 103					.
				кмоль				кмоль
Ответ: 4,15 10	3			Дж		, 4,15 10	3		Дж		, 16,6	10	3		Дж	.
Ответ: 4,15 10						, 4,15 10					, 16,6	10				.
			кмоль К						кмоль					кмоль

Задача 9

Некоторое количество идеального газа расширяется так, что процесс на диаграмме p,V изображается прямой линией, проходящей через начало координат.

а) чертим диаграмму p, V.

Решение:

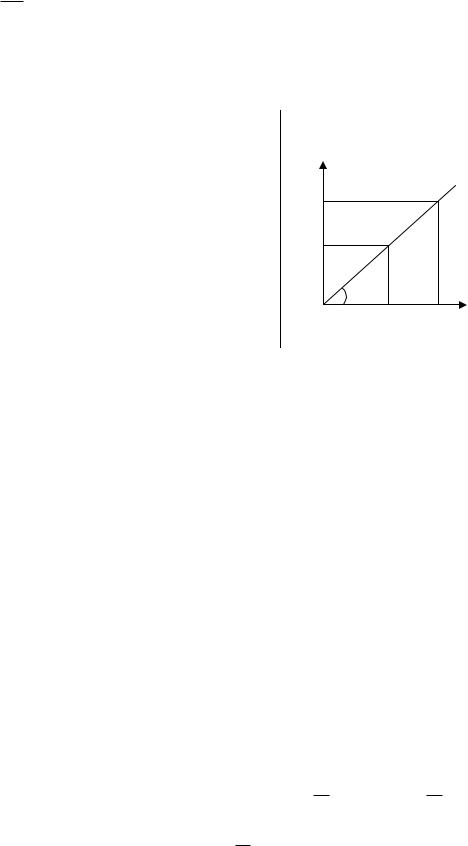
Известны: начальный объём газа V1, начальное давление p1 и отношениеСрСv . В результате расширения объём газа увеличился в три раза.

Найти: а) показатель политропы n,

б) приращение внутренней энергии ∆U газа, в) работу A, совершаемую газом,

г) молярную теплоемкость C газа при этом процессе. Дано:

p1	p
γ	p2
V2=3V1	p2
V2=3V1
n=?	p1
∆U=?	p1
∆U=?
A=?
C=?	α
	рис.9	V1 V2	V
	рис.9

Уравнение политропического процесса записывается формулой pVn=const или p1V1n= p2V2n, где n –показатель полиропы. Согласно условию задачи зависимость p от V изображается прямой линей. Уравнение прямой линии p=αV, где коэффициент α равнее тангенсу угла наклона прямой к оси V. a=tgα. Соответственно p1=aV1 и p2=aV2. Подставив значение p1 и p2 в

уравнение политропы: aV1 V1n aV2V2 n , получаем V1n 1 V2 n 1 .

По условию задачи V2 3V1 . Тогда V1n 1 3V1 n 1 или 1 3n 1 . Приравниваем показатели степеней 0=n+1. Отсюда показатель политропы n=-1. Уравнение рассматриваемого процесса теперь можно записать так: pV1 const или

	p	const .
		const .
V
б) Приращение внутренней энергии газа
U			m		i	R T , где i- число степеней свободы,	m	- число кмолей,
U						R T , где i- число степеней свободы,		- число кмолей,
				2			1
R – универсальная газовая постоянная, рассчитанная на кмоль газа,
- изменение температуры газа в данном							процессе. Величину		m	R T
- изменение температуры газа в данном							процессе. Величину			R T

можно найти, записав уравнение Менделеева-Клапейрона для начального и конечного состояния газа, а именно p1V1 m RT1 , p2V2 m RT2 . вычитая одно

уравнение из другого ,получим m R(T2 T1 ) p2V2 p1V1 . Объем V2 3V1 по условию задачи. Находим соотношение между р1 и р2.

Для рассматриваемого процесса									p1		p2	. Отсюда			p		p1V2			p1 3V1	3 p .
Для рассматриваемого процесса												. Отсюда			p	2					3 p .
									V1		V2					2		V1		V1		1
									V1		V2							V1		V1
Давление			p		3 p . Тогда	m	R(T T ) 3 p 3V p V 9 p V p V 8 p V и
Давление			p		3 p . Тогда		R(T T ) 3 p 3V p V 9 p V p V 8 p V и
				2	1			2		1	1		1	1	1		1	1	1	1	1	1
				2	1			2		1	1		1	1	1		1	1	1	1	1	1
U	i	8 p V			. Находим i. Коэффициент Пуассона											C p	равен отношению


	2	1	1													CV
	2															CV

теплоемкостей газа (удельных или молярных соответственно) при постоянном давлении и при постоянном объеме. Учитывая, что удельные

C p

i 2

теплоемкости c

и c

, и что молярные теплоемкости C

R и

R , имеем

i 2

. Отсюда

и U

8 p1V1

в) бесконечно малая работа dA, совершаемая газом, выражается формулой dA=pdV. Вся работа А газа равна сумме элементарных работ, т.е. A dA pdV . Но под знаком интеграла стоят две переменные величины p

и V. Находим зависимость давления p от объема V.

Рассматриваемый процесс изображается на диаграмме p, V прямой линией,

т.е. p=aV,

где a=tgα (см. рис.9). Из чертежа видно,

что

Тогда

p1V2

V .

Теперь

A pdV

VdV

(V2

V1 )

(9V1 V1 )

4 p1V1 .

1 V

A=4p1V1.

г) количество тепла, сообщенного газу,

C T . Из этой формулы можно

найти молярную теплоемкость С газа, но для этого надо знать, чему равны

величины

Q и

T .

R T было уже найдено в данной задаче в пункте б).

R T 8 p V . Отсюда

8 p1V1

. Находим

Запишем первое начало

термодинамики

Q U A .

данной

задаче

уже было

найдено, что

8 p1V1

A=4p1V1.

Тогда

8 p1V1

4 p V

Подставляем

1 1

1 1 1

найденные

значения

формулу

C T , получим

4 p V

8 p1V1

. Отсюда

1 1 1

2 1

Ответ: а)n=-1; б) U

8 p1V1

; в) A=4p1V1; г) C

2 1

<<< < Предыдущая 12 / 22

Соседние файлы в папке РАЗДЕЛ №2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

#
27.11.20241.05 Mб91 Презентация лекции по теме МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ.pdf
#
27.11.2024403.4 Кб72 Конспект лекции на тему ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ ИДЕАЛЬНОГО ГАЗА.pdf
#
27.11.2024400.13 Кб82 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ НА ТЕМУ СТАТИСТИЧЕСКАЯ ФИЗИКА.pdf
#
27.11.20241.14 Mб72 Презентация лекции по теме ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ.pdf
#
27.11.2024339.75 Кб83 Конспект лекции на тему ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ.pdf
#
27.11.2024560.91 Кб73 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ НА ТЕМУ ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ.pdf
#
27.11.20241.2 Mб83 Презентация лекции по теме ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ.pdf
#
27.11.20241.12 Mб83 Презентация лекции по теме ЦИКЛИЧЕСКИЕ ПРОЦЕССЫ. ТЕПЛОВАЯ МАШИНА.pdf
#
27.11.2024469.91 Кб74 Конспект лекции на тему ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.pdf
#
27.11.2024477.35 Кб74 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ НА ТЕМУ ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.pdf
#
27.11.20241.27 Mб74 Презентация лекции по теме ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.pdf