В соответствии с преобразованиями Галилея скорость тела относительно Земли будет:
x ' 4 105 км/с,
Положение СТО: скорость света
является предельной скоростью переноса информации, вещества и взаимодействий:
с 2,998 108 м с 1.
Оценим скорость тела, используя преобразования Лоренца.
Внутри корабля перемещение dx' за время dt' равно dx' 'dt'.
С точки зрения наблюдателя на Земле:
't' dt |
dy = dy'; dz = dz'; |
||||||||
dx |
|
|
|
||||||
1 2 |
dt' |
'dt' |
|||||||
|
|
|
|
||||||
|
|
|
|
c2 |
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
dt |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 2 |
|||||
Так как x |
|
dx |
|
то: |
|
|
|
'dt' dt' |
|
|||
dt |
x |
|
; |
|||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
'dt' |
|||||||
|
|
|
|
|
|
|
dt' |
|
||||
|
|
|
|
' |
|
|
c2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
1 ' |
|
|
|
|
|
|
|||
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
Правило сложения скоростей в
релятивистской кинематике.
В нашем примере в соответствии полученной формулой:
x |
|
2 105 2 105 |
2,8 10 |
5 |
км/с. |
||
|
|
10 |
|
||||
|
|
1 |
4 |
10 |
|
|
|
|
|
|
9 |
1010 |
|
|
|
При медленных движениях ( c) получаем нерелятивистские формулы, соответствующие преобразованиям Галилея.
При движении со скоростью света:
c cc2 c. 1 c2
Одновременность событий в СТО
По Ньютону, если два события происходят одновременно, то это будет одновременно для любой системы отсчета (время абсолютно). Эйнштейн задумался, как доказать одновременность?
Возьмем два источника света на Земле А и
В.
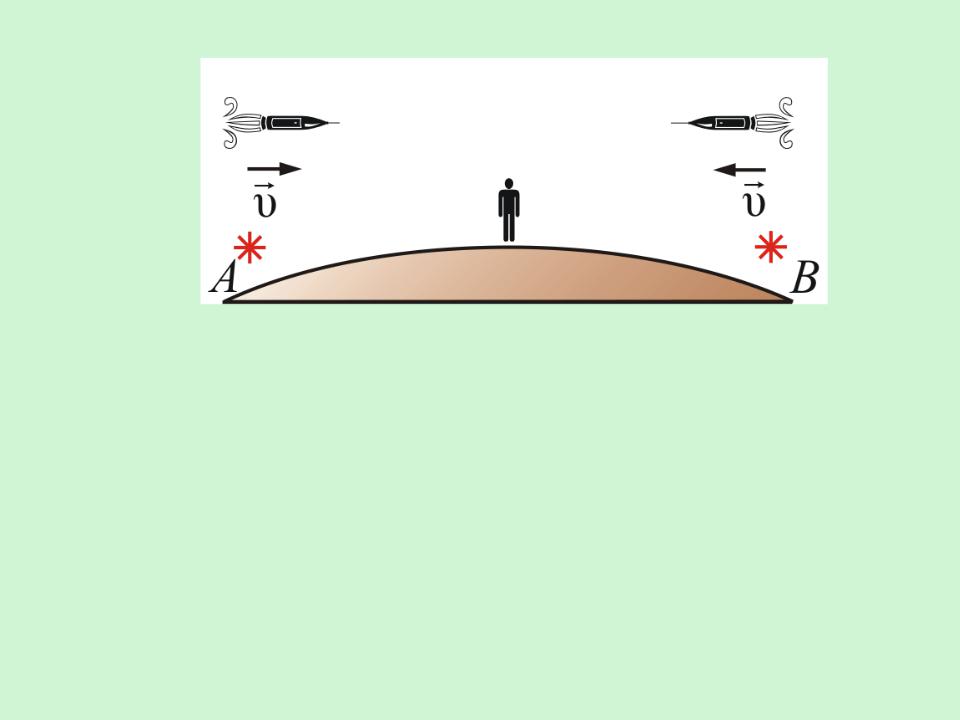
Если свет встретится на середине АВ, то вспышки для человека находящегося на Земле, будут одновременны. Но со стороны пролетающих мимо космонавтов со скоростью υ вспышки не будут казаться одновременными, т.к. . c const
Рассмотрим это более подробно.
Пусть в системе k (на Земле) в точках x1 и x2
происходят одновременно два события в момент
времени t1 t2 t.
Будут ли эти события одновременны в k' (в пролетающей мимо ракете)?
Для определения координат в k' воспользуемся преобразованиями Лоренца
x' |
|
|
x t |
x'2 |
x2 t |
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
||||||||||||||
1 2 |
|
|
||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
соответствии |
с преобразованиями |
||||||||||||||||||||||||
Лоренца для времени в системе k' получим: |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
t |
|
x1 |
|
|
t |
x2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|||||||||
t'1 |
|
c2 |
t'2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
2 |
|
1 2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
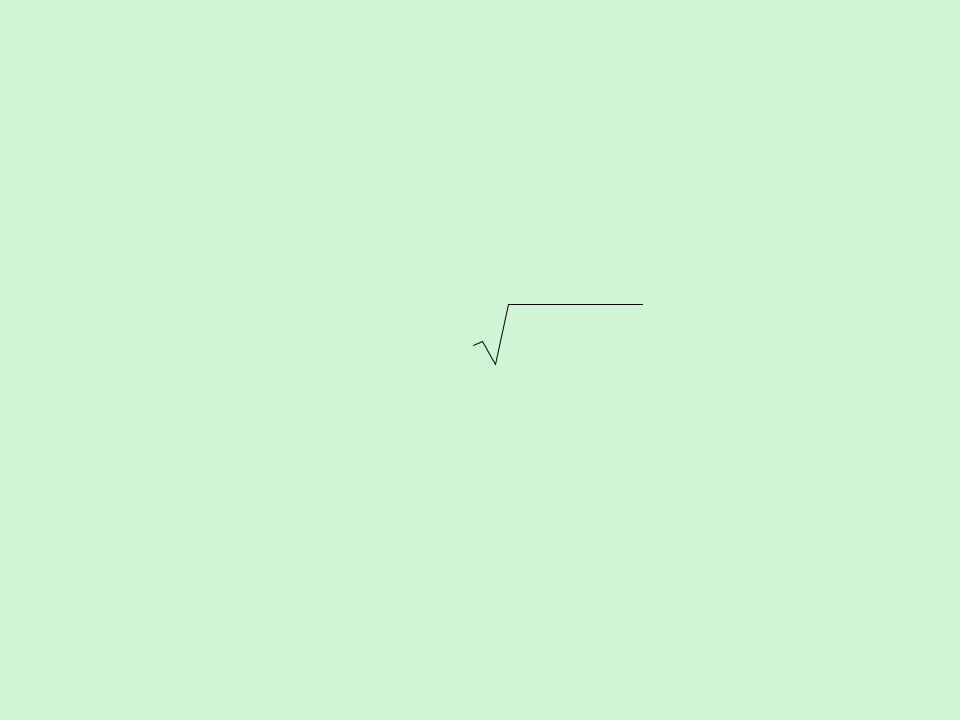
Определим интервал времени между событиями в k':
t' t' (x1 x2 )
2 1 c2 1 2
.
Разница во времени будет зависеть от υ и она может отличаться по знаку (ракета подлетает с той или другой стороны).