Сегодня: среда, 27 Ноябрь, 2024

Динамика вращательного движения твердого тела

Вращательным движением твердого тела будем называть такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и ой же прямой, называемой осью вращения.

Для изучения динамики вращательного движения к известным кинематическим величинам добавляются ещё три величины:

момент инерции (J), момент силы (M) и

момент импульса (L)

Момент инерции

Разобьем тело на такие малые части, что каждую из них можно считать материальной точкой. Пусть mi – масса i – ой

материальной точки, ri – ее

расстояние до некоторой оси O.

Величина, равная произведению массы материальной точки на квадрат расстояния ее до данной оси, называется моментом инерции

материальной точки относительно оси:

Ii miri2

Сумма моментов инерции всех материальных точек тела называется

моментом инерции тела

относительно некоторой оси:

n

I miri2

i 1

интегрального исчисления согласно формуле I r2dm

где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами x,y,z.

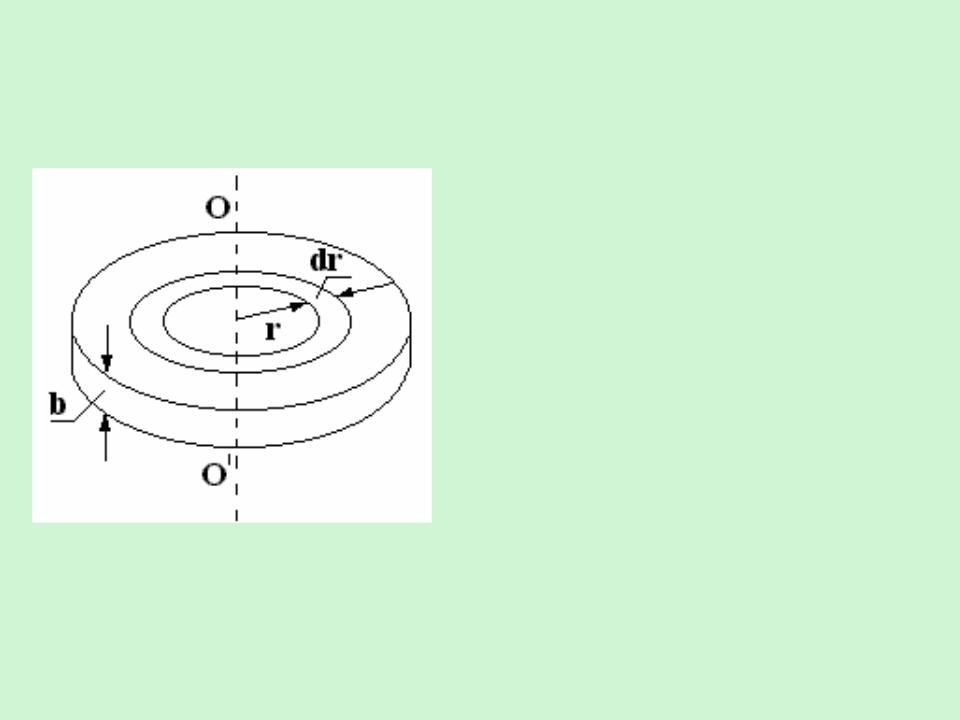
В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр.

где b - толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова и масса

элементарного слоя

dm 2 rb dr

находим момент инерции

R

I r2b2 rdr