Файловый архив студентов. Файловый архив студентов.
1295 вузов, 5022 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Томский Политехнический Университет
Предмет:
Физика общая
Файл:

Физика / 1 семестр / РАЗДЕЛ №1. МЕХАНИКА / 5 Конспект лекции на тему ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

.pdf
Скачиваний:
4
Добавлен:
27.11.2024
Размер:
425.25 Кб
Скачать
☆

Тема 5 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

5.1. Момент инерции твердого тела

При изучении вращения твердых тел будем пользоваться понятием момента инерции.

Разобьем тело на такие малые части, что каждую из них можно считать материальной точкой (рис. 5.1). Пусть mi – масса i-й материальной точки, ri – ее расстояние до некоторой оси O O .

Величина, равная произведению массы материальной точки на квадрат кратчайшего расстояния ее до данной оси, называется моментом инерции материальной точки относительно оси:

I

i

m r2 .

(5.1)

 

i i

 

Сумма моментов инерции всех материальных точек тела называется

моментом инерции тела относительно некоторой оси:

 

 

n

 

 

 

I miri2 .

 

 

(5.2)

i 1

Момент инерции твердого тела зависит, как нетрудно видеть, от распределения масс относительно интересующей нас оси.

Если тело представляет собой обруч массы m, толщина которого мала по сравнению с радиусом R,

то момент его инерции относительно оси, b проходящей через центр и перпендикулярной к плоскости обруча, равен

I miri2 mi R2 R2 mi mR2

O

i

i

i

 

.

 

 

 

 

O

dr

r

O’

Рис. 5.2

(5.3)

 

Для тел более сложной формы суммирование

ri

выражения

(5.2)

производится

методами

mi

интегрального исчисления согласно формуле

 

I r 2dm ,

 

(5.4)

 

V

 

 

 

O’

где интегрирование производится по всему объему тела.

Рис. 5.1

Величина r

в этом случае есть функция

положения

точки с координатами x, y, z.

 

 

 

В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 5.2). Разобьем диск на кольцевые слои толщиной dr.

Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r. Объем такого слоя равен

dV b 2 r dr ,

где b – толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова и

dm dV 2 r b dr ,

где dm – масса кольцевого слоя.

Теперь по формуле (5.4) находим момент инерции

R

 

 

 

I r2 b 2 r dr ,

 

 

 

0

 

 

 

 

 

где R – радиус диска;

 

 

 

R

R

4

 

I 2 b r3dr 2 b

 

.

4

0

 

 

 

 

 

 

 

 

Наконец, введя массу диска m, равную произведению плотности на

объем диска b R2 , получим

 

 

 

I

mR2

.

 

(5.5)

 

 

2

 

 

 

 

Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр масс тела, приведены в табл. 5.1.

 

 

Таблица 5.1

 

 

 

 

Твердое тело

Ось вращения

Момент инерции

 

Тонкий стержень длины

Перпендикулярна стержню

1 12 m 2

 

и проходит через центр тяжести

 

 

 

 

Сплошной цилиндр

Совпадает с осью цилиндра

1 2 mR2

 

радиуса R

и проходит через центр тяжести

 

 

 

Тонкий диск радиуса R

Совпадает с диаметром диска

1 4 mR2

 

Шар радиуса R

Проходит через центр тяжести

2 5 mR2

 

 

шара

 

 

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то можно найти момент инерции относительно любой другой параллельной оси. Для этого надо воспользоваться теоремой Гюйгенса – Штейнера:

момент инерции тела I относительно произвольной оси равен моменту его инерции Ic относительно параллельной ей оси, проходящей через центр масс C тела, сложенному с произведением массы тела m на квадрат расстояния a между осями:

I I

c

ma2 .

(5.6)

 

 

 

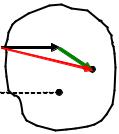
Найдем связь между моментами инерции тела относительно двух параллельных осей, одна из которых проходит через центр масс. Найдем момент инерции тела относительно оси z, параллельной оси zC. Ось zC проходит через центр масс тела. Разделим мысленно тело на частицы массой mi, где i – порядковый номер. Определим положение каждой частицы относительно осей z

и zC. В соответствии с определением момента инерции Ii miri2 , где ri – это

кратчайшее расстояние до оси вращения (радиус окружности, которую описывает точка при своем движении вокруг оси вращения).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

На рис. 5.3 видно, что

ri ri r0

,

 

тогда момент инерции точки массой mi

относительно оси z

равен I

i

m r 2 ,

а для всего тела

 

z

 

zC

 

 

 

 

 

 

 

 

 

i i

 

 

 

 

 

 

 

 

 

момент

инерции относительно

оси

 

 

z

 

равен

сумме

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

моментов инерции всех частиц тела относительно этой

 

r0

 

 

же оси:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ri

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ri

 

mi

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

C

I z Ii miri

 

mi (ri r0 )

 

 

 

а

 

 

 

 

i

i

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

miri2 mir02

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 mi (ri r0 ).

 

 

 

 

 

 

 

i

 

i

 

 

 

i

 

 

 

 

 

 

 

 

 

 

Рис. 5.3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(5.7)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

По определению I z

C

miri2

 

– момент инерции тела относительно оси zC,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

проходящей через центр масс тела;

mi

m , тогда mir02

ma2 . Выражение

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 mi (ri

r0 )

можно преобразовать:

 

2 mi (ri r0 ) 2( miri r0 ) .

 

Величина,

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

равная miri

mrC

, определяет положение центра масс тела относительно оси

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

zC. Из рисунка видно, что

0 , т.к. центр масс лежит на оси zC.

 

 

rC

 

 

Тогда получим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

z

I

z

 

ma2

 

 

 

(5.8)

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

– момент инерции Iz тела относительно произвольной оси равен сумме момента инерции тела I zC относительно параллельной ей оси zC, проходящей через

центр масс, и величины ma2, где m – масса тела, a – расстояние между осями.

Пример 1. Момент инерции тонкого стержня (массы m и длины ) относительно оси, перпендикулярной стрежню и проходящей через его конец, равен

 

1

 

2

 

2

 

1

 

 

2

 

 

I

 

 

m

 

m

 

 

 

 

 

m

 

.

(5.9)

 

 

 

 

 

 

 

 

12

 

 

 

2

 

3

 

 

 

 

 

 

В

 

5.2. Кинетическая энергия

 

 

 

 

 

вращательного движения твердого тела

r

 

 

 

 

 

 

 

 

 

 

 

 

M

 

 

 

Пусть твердое тело вращается вокруг неподвижной оси

 

 

 

 

О

d

 

 

ОО (рис. 5.4). Мысленно разобьем тело на материальные точки

 

 

 

массой mi. Каждая материальная точка движется по окружности

 

 

F

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 5.5

 

радиуса ri с линейной скоростью vi . Кинетическая энергия

 

 

 

 

вращающегося тела равна сумме кинетических энергий

 

O

 

 

этих точек:

 

 

 

 

m v 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Eк

 

 

 

 

 

m1

 

 

 

 

 

i

i

.

 

(5.10)

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Линейная скорость материальной точки зависит

 

 

r1

 

 

 

 

от расстояния до оси вращения ri:

 

 

 

 

 

 

 

vi

 

 

 

 

 

 

 

 

 

 

vi ri ,

 

 

 

(5.11)

 

 

ri

mi

где – угловая скорость тела.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

n

 

 

 

 

vi

 

Отсюда Eк

 

2

, т.к. I

 

 

2

, то

 

 

 

 

2

miri

miri

 

 

 

 

 

i

 

 

 

 

 

i 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

O

 

 

 

 

Eк

I

2

 

 

 

 

 

 

 

 

 

 

 

,

 

 

 

(5.12)

 

Рис. 5.4

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где I – момент инерции тела относительно оси

 

 

 

 

вращения; – его угловая скорость.

 

 

 

 

 

 

 

 

 

 

В

случае плоского движения тела,

например

шара,

скатывающегося с

наклонной плоскости без скольжения, энергия складывается из энергии поступательного движения и энергии вращения:

E

mvc2

 

Ic 2

,

(5.13)

 

 

к

2

2

 

 

 

 

 

где m – масса тела; vc – скорость центра масс тела; Ic – момент инерции тела

относительно оси, проходящей через его центр масс; – угловая скорость тела.

 

5.3. Момент силы

 

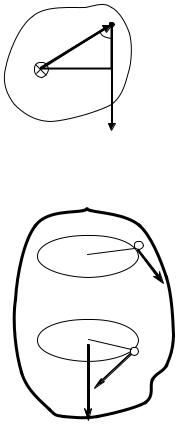
Рассмотрим вращение тела вокруг неподвижной оси (рис. 5.5). Пусть сила

 

F

лежит в плоскости, перпендикулярной к оси вращения 0; r – радиус-вектор

точки приложения силы относительно оси вращения; d – кратчайшее расстояние от оси вращения до линии действия силы, называемое плечом силы.

Векторная величина, численно равная произведению силы на плечо,

называется моментом силы относительно оси вращения:

 

M F d .

(5.14)

Как видно из рисунка:

d r sin ;

M F r sin ,

т.е. в векторном виде

 

 

 

 

 

.

(5.15)

 

 

M rF

 

 

 

 

 

 

Направление M совпадает

с

направлением

 

поступательного

движения

 

 

 

 

 

 

 

винта при его вращении от r к

F (в нашем примере вдоль оси вращения «от

нас»).

 

 

 

 

 

 

В частном случае, когда 0,

M 0 (линия действия силы пересекает ось

вращения). Такая сила уравновешивается реакцией опоры и вращения не вызывает.

5.4. Уравнение динамики вращательного движения твердого тела

Пусть тело вращается вокруг оси О под действием силы F (рис. 5.6). Найдем работу этой силы.

При повороте тела на бесконечно малый угол d точка приложения силы B проходит путь

d r d ,

где r – радиус окружности, описываемой точкой B. Элементарная работа равна

 

 

 

 

 

dA F r d F r dt .

 

(5.16)

 

 

B

Эта

работа идет на увеличение

кинетической

O

r

 

 

 

 

 

 

 

 

 

I 2

d

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Eк

 

 

энергии

вращающегося

тела. Так как

 

, а

 

d

2

 

F

dA dEк , то

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I 2

 

 

 

 

 

 

 

 

 

dE

d

 

 

I

d .

 

(5.17)

 

 

 

 

 

 

 

Рис. 5.6

 

 

к

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

Поэтому F r dt I d.

 

 

 

Радиус окружности r является плечом силы F, следовательно, M F r и

 

 

 

 

Mdt Id,

 

 

 

(5.18)

или

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M I

d

I .

 

 

(5.19)

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

 

 

 

 

 

 

имеют одинаковое направление, придем к

Учитывая, что векторы M

и

соотношению

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(5.20)

 

 

 

 

M

I .

 

 

 

Это – основное уравнение динамики вращательного движения вокруг неподвижной оси. Оно напоминает второй закон Ньютона для поступательного

L

miv i

О ri

Рис. 5.7

(сравним

с формулой

 

 

 

dA (F

dr ) ).

движения. Роль массы играет момент инерции I, роль

линейного ускорения – угловое ускорение , роль

силы – момент силы M .

Из этого уравнения, в частности, видно, что момент инерции I определяет инерционные

свойства тела при вращении: при одном и том же

значении момента сил M тело с большим моментом инерции приобретает меньшее угловое

ускорение . Заметим, что работа при вращении тела согласно (5.16) равна dA F r d F r dt .

На

 

 

 

 

 

 

или

рис. 5.6 сила F r , поэтому

M rF

M F r . С другой стороны,

 

 

– угловое

d dt

 

 

 

 

направлены по

перемещение. Векторы M и

d

 

 

 

 

или

 

 

 

одной прямой, поэтому dA (M d )

 

 

 

 

dA M d

 

 

 

 

 

(5.21)

для

работы при поступательном движении

тела

5.5. Момент импульса

Рассмотрим движение отдельных точек тела, вращающегося вокруг неподвижной оси (рис. 5.7). Каждая из них массой mi движется по окружности

 

 

 

постоянного радиуса ri. Ее линейная скорость vi , импульс

mi vi . Скорость и

 

 

 

импульс перпендикулярны радиусу, т.е. радиус является плечом вектора

mi vi .

Поэтому можно записать, что момент импульса данной точки равен

Li mi vi ri ,

и направлен по оси вращения в сторону, винта. Учитывая, что vi ri , получим

L r P

(5.22)

i

i i

 

определяемую

правилом правого

L m r2 I

,

(5.23)

i

i i

i i

 

 

где Ii – момент инерции материальной точки mi

относительно оси вращения.

Момент импульса твердого тела относительно оси равен сумме моментов импульсов всех его точек:

L Ii ,

i

или

L miri2 miri2 I .

(5.24)

i

i

Итак, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно этой же оси на угловую

скорость.

 

 

 

 

 

 

придем

Учитывая, что векторы L

и имеют одинаковое направление,

к соотношению

 

 

 

 

 

 

(5.25)

 

 

L I .

При описании динамики вращательного движения момент импульса играет такую же роль, что и импульс при поступательном движении.

Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (табл. 5.2).

Таблица 5.2

Поступательное движение

Вращательное движение

 

 

 

 

Масса

m

 

 

 

 

Момент инерции

 

I

 

 

Скорость

 

 

 

 

 

Угловая скорость

 

 

 

 

 

 

dr

 

 

d

 

v

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

dt

Ускорение

 

 

 

 

 

 

Угловое ускорение

 

 

 

 

 

 

dv

 

d

 

a

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

dt

Сила

 

 

 

 

 

 

 

Момент силы

 

 

 

 

 

 

 

F

 

 

 

 

 

M

 

 

 

 

Импульс

 

 

 

 

 

 

Момент импульса

 

 

 

 

 

P

mv

 

L I

Основное уравнение

 

 

 

 

 

 

Основное уравнение динамики

 

 

 

 

 

F

ma

 

M I

динамики

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Работа

dA FS dS

Работа

dA Md

 

 

 

 

 

 

 

 

 

 

Кинетическая энергия

 

mv 2

 

Кинетическая энергия

 

I 2

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 
Соседние файлы в папке РАЗДЕЛ №1. МЕХАНИКА
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности