Добавил:

PickyEater13 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

Физика общая

Файл:

4 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ НА ТЕМУ РАБОТА И ЭНЕРГИЯ

.pdf

Скачиваний:

Добавлен:

27.11.2024

Размер:

844.36 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

РАБОТА СИЛЫ. МОЩНОСТЬ

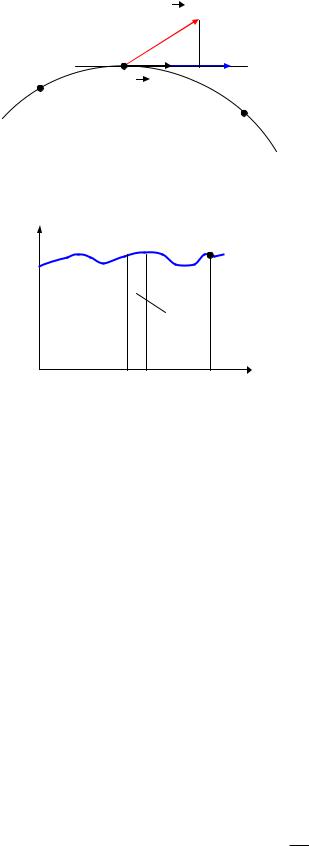
Пусть тело под действием силы F совершает перемещение по некоторой

траектории 1 – 2. В общем случае сила F

в про-

цессе движения тела может меняться как по моду-

лю, так и по направлению.

Рассмотрим

элементарное

перемещение,

пределах которого силу F можно считать посто-

янной.

Элементарной работой силы

F на перемеще-

нии dr называется скалярная величина

(1)

dA F dr F cos dS F dS ,

где – угол между векторами

–

и dr , dS

F cos .

элементарный путь,

FS – проекция вектора F

на вектор dr ,

Сила

, действующая на материальную точку, как правило, изменяется по

мере перемещения материальной точки по траектории относительно системы

отсчета (сила может зависеть как от координат x, y, z точки, так и от скорости

движения точки). Таким образом, сила					F в общем случае – функция несколь-
ких переменных.			Поэтому элементарная работа силы				не является полным
ких переменных.			Поэтому элементарная работа силы			F	не является полным
дифференциалом какой-либо функции координат точки.							Чтобы это подчерк-
нуть, элементарная работа обозначается символом A , а не dA .

	В	прямоугольных декартовых			координатах	F	Fxi	Fy j	Fz k ,	а

dr	dxi	dyj dzk . Поэтому согласно правилу скалярного умножения векто-
				равна: A Fx dx Fy dy Fz dz , где Fx , Fy , Fz
ров, элементарная работа силы F				равна: A Fx dx Fy dy Fz dz , где Fx , Fy , Fz

– проекции силы			F на оси координат, dx,dy,dz – проекции вектора перемеще-
		на оси координат.
ния dr		на оси координат.

	Работа А, совершаемая силой			F на конечном перемещении материальной
точки из положения 1 в положение 2, равна сумме элементарных работ силы
										F
на всех малых участках траектории материальной точки от 1 до 2.									Суммируя

(интегрируя) выражение (1) по всем элементарным участкам пути от точки 1 до точки 2, найдем работу силы F на данном пути:

2		2
A Fdr		FS dS .	(2)
1		1
Если сила имеет постоянные величину и направление, а движение прямо-
линейное, то проекцию вектора силы FS	в выражении для работы можно выне-
сти за знак интеграла, в результате чего получится формула:
	2
A FS dS FS S F S cos .			(3)
	1

Движение по участку траектории.

		F
		FS
	dr	v
1	dr
1		2
		2

r2	2
A12 Fdr	FS dS.
r1	1
FS – проекция вектора			на вектор
FS – проекция вектора		F	на вектор

перемещения dr

Единица работы в СИ – джоуль (Дж). 1 Дж – работа, совершаемая силой

1 Н на пути 1 м (1 Дж = 1 Н м ).

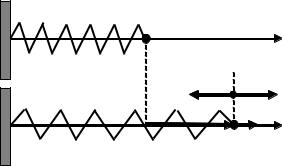
		При графическом изображении FS(S) ра-
F S		бота равна площади под кривой.
		бота равна площади под кривой.

		d A
0
0	d S	S
	d S

Для характеристики скорости, с которой совершается работа, вводят вели-

чину, называемую мощностью. Мощность – это работа, совершаемая силой

за единицу времени. Средняя мощность за промежуток времени

ср

Если за время dt сила F

совершает работу F dr , то мощность, развивае-

мая этой

силой в данный

момент времени (мгновенная мощность)

есть

(Fdr )

. Учитывая, что

v , получим:

(4)

N F

Таким образом, мгновенная мощность, развиваемая силой

F ,

равна

скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения данной силы.

Как и работа, мощность – скалярная величина. Единица мощности в СИ – ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж

(1 Вт = 1 Дж/с).

Выразим работу А силы на конечном пути через мгновенную мощность N.

Так как мгновенная мощность N dtA , то элементарная работа A Ndt , тогда

2	t2

A (Fdr ) Ndt , где t1		и t2 – моменты времени, соответствующие пребыва-
1	t1

нию материальной точки в точках 1 и 2 траектории движения.

Работа силы тяжести. Пусть тело массой m перемещается вдоль произвольной траектории из точки 1 в точку 2. При этом на тело (материальную точку) действует постоянная сила тяжести

mg .

Работа

силы

тяжести

равна:

Мысленно разделим всю

A (mg dr ) .

траекторию на элементарные участки и

вычислим

элементарную

работу

на

одном из

них:

A (mg dr )

cos mg dz ,

A (mg

dr ) mg

где α – угол между векторами

, dz – приращение координаты z тела, со-

g и

, При перемещении тела из точки 1 в точку

ответствующее его перемещению dr

2 траектории координата z изменяется в пределах от z1

до z2. Тогда работа силы

mg dz mg(z1

z2 ) .

тяжести равна: A A (mg

dr )

Из полученной формулы видно, что работа силы тяжести не зависит от формы траектории движения тела, а определяется только ее координатой z

в начальном и конечном положении.

Работа гравитационной силы. Пусть в точке О пространства находится тело (материальная точка) массы M, которое действует на тело (материальную точку) массой m с силой гравитационного

									Mm
						взаимодействия Fгр :		Fгр			r ,
	m					взаимодействия Fгр :		Fгр	r	2	r ,
1	m		dr						r
						где r – единичный вектор, направленный
		F			2		, γ – гравитационная посто-
r		гр	r	dr	2	по вектору r	, γ – гравитационная посто-
						янная.
r1						янная.
r						Если тело переместилось из точки 1
				r2		в точку 2 траектории под действием гра-
						в точку 2 траектории под действием гра-
О M						витационной	силы	взаимодействия, то
О M						работа гравитационной силы на этом пу-
						работа гравитационной силы на этом пу-

		2		Mm
ти равна:	A		(Fгрdr )		( r dr ) .
				r 2

		1
Работа δА гравитационной силы на элементарном перемещении
из	элементарных					участков	траектории)

dr (одном равна

A (Fгрdr )

( r dr )

cos

где величина

r 2

cos

равна приращению dr модуля радиус-вектора r .

При перемещении тела из точки 1 в точку 2 модуль его радиус-вектора из-

меняется от

до r2

, поэтому работа гравитационной силы на пути между точ-

ками 1 и 2 равна:

(Fгрdr )

dr Mm

(

r 2

) .

Работа гравитационной силы не зависит от формы траектории, а определяется только начальным и конечным положением тела относительно другого тела.

				Работа	упругой	силы.	Рас-
О	Fупр 0			смотрим пружину, один конец кото-
			x
				рой закреплен, а другой может пере-
				мещаться горизонтально под дей-
Fупр kr		Fвнешн		ствием внешней силы. Направим ко-
				ординатную ось x параллельно оси
		dr		пружины и выберем начало отсчета
О			x
				координаты x (x = 0) в положении
	r

				незакрепленного конца		недеформи-
				рованной пружины (точка О).

При растяжении или сжатии			пружины возникает упругая сила Fупр				kr ,

где r – радиус-вектор, проведенный из точки О к незакрепленному концу де-

формированной пружины. Под действием внешней силы Fв неш, работу которой

рассматривать не будем, незакрепленный конец пружины, к которому прило-

жена также	Fупр , переместится на	dr . Если незакрепленный конец пружины

переместился вдоль оси x из точки с координатой x1 в точку с координатой x2,

				2	2
то работа	Fупр	равна: A A				(Fупрdr )
				1	1
2		x2	k
			k
A ( krdr ) kxdx				(x12	x22 ) .
A ( krdr ) kxdx			2	(x12	x22 ) .
1		x1	2
1		x1

( krdr ) или в проекции на ось x

Из полученного выражения видно, что работа упругой силы на конечно

пути зависит только от начальной x1 и конечной x2 координат точки приложения силы.

Работа силы трения скольжения. Рассмотрим тело массой m, движущееся по горизонтальной поверхности под действием внешней силы Fв неш по про-

извольной криволинейной траектории из точки 1 в точку 2. При перемещении тела относительно поверхности между соприкасающимися телами возникает

сила трения скольжения Fтр.ск N mg , где – коэффициент трения скольжения, а N – модуль силы нормальной реакции опоры ( N mg ).


	N
Fтр	N
Fтр
1		Fвнеш 2

	mg

		Fвнеш	2
			2
Fтр
		dr

вид сверху

Работа силы трения скольжения на одном из элементарных участков траектории равна:

			A (F	dr ) F		dr	cos1800 mg dS ,
			A (F	dr ) F		dr	cos1800 mg dS ,
			тр.ск	тр.ск
где	dr	dS – модуль вектора элементарного перемещения равен элемен-
где	dr	dS – модуль вектора элементарного перемещения равен элемен-
тарному пути			dS . В любой момент времени вектор силы трения скольжения

Fтр.ск направлен противоположно dr					. Если тело перемещается из точки 1 в

точку 2, то работа силы трения будет равна:

A A

(Fтр.ск dr ) kmg ds kmgS ,

где S – пройденный телом путь по траектории.

В отличие от работы силы тяжести, гравитационной силы и упругой силы,

работа силы трения зависит от длины пройденного телом пути S, и, следовательно, зависит от формы траектории.

Таким образом, среди рассмотренных сил можно выделить такие, работа которых не зависит от формы траектории и характера движения тела, а определяется только начальным и конечным положением относительно других тел. Это – сила тяжести, гравитационная сила, упругая сила.

Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положением относительно других тел, называются консервативными.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ

Следствием действия силы на материальную точку является приобретение


			dv
материальной точкой ускорения: ma	F	или m		F	,
			dt

где F – результирующая сила, действующая на материальную точку.

Пусть частица массы m движется под действием

некоторой силы

F .

Найдем элементарную работу этой силы на перемещении dr .

A F dr m a dr

dr m v dv

так как F

m a ,

dv v dv .

Таким образом,

mv 2

A mv dv d

Если материальная точка перемещается из состояния 1 в состояние 2. Состояние 1 материальной точки характеризуется скоростью v1 , а состояние 2 ха-

рактеризующееся скоростью v2 . Работа результирующей силы при переходе

материальной

точки

из

состояния

состояние

равна:

A A mvdv mv2

mv1

Выражение

mv 2

называется

кинетической

энергией

материальной

точки. Кинетическая энергия является скалярной мерой движения.

Итак, работа результирующей силы равна приращению кинетической энергии материальной точки.

В интегральной форме данное утверждение записывается в виде:

		mv 2	mv 2					E
A		2			1	или A					.
A						или A				к	.
1 2		2		2		1 2				к
		2		2
						mv 2
									или			A dEк .

В дифференциальной форме – в виде: A d							2
							2
Уравнения A1 2 Eк	и A dEк			называются теоремами об изменении

кинетической энергии (в интегральной и дифференциальной формах соответственно).

Согласно теореме, изменение кинетической энергии материальной точки обусловлено тем, что результирующая сила совершает работу. Изменение кинетической энергии означает изменение модуля скорости тела.

Таким образом, кинетическая энергия это механическая энергия, которой

обладает тело массой m, движущееся со скоростью v .

E			mv 2	.
	K
		2

При конечном перемещении из точки 1 в точку 2 работа силы идет на приращение кинетической энергии:

2	2
A12 dA dEК EК 2 EК1 ,
1	1

A12 EK 2 EK1 .

(5)

Если A12 0, то EK 2 EK1 , т.е. кинетическая энергия частицы увеличивается; если же A12 0 , то кинетическая энергия уменьшается.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Если на тело (материальную точку) в каждой точке пространства действует определенная сила, то всю совокупность сил называют силовым полем. Если силы не зависят от времени, силовое поле называется стационарным.

Пусть взаимодействие между телами осуществляется с помощью силовых полей (например, поле гравитационных сил, поле упругих сил), которые обладают следующим свойством: работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от траектории тела, а зависит только от начального и конечного положения тела. Такие силы называются консервативными. Поле консервативных сил называется консервативным.

Если работа, совершаемая силой, зависит от траектории тела, то такая сила называется неконсервативной; ее примером является сила трения.

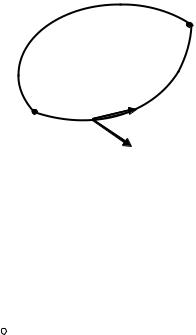
Покажем, что при перемещении тела в консервативном поле работа консервативных сил по замкнутой траектории равна нулю.

Работа консервативной силы не зависит от вида траектории точки между ее начальным (1) и конечным (2) положениями, ни от закона движения матери-

a		альной точки по траектории: A1 a 2 A1 b 2 A1 2 ,
a		где A1 a 2 и A1 b 2 – работа консервативной сила
	2	где A1 a 2 и A1 b 2 – работа консервативной сила
	2	при перемещении материальной точки из 1 в 2 по
		при перемещении материальной точки из 1 в 2 по
		траекториям 1–а–2 и 1–b–2. Изменение направле-
		ния движения материальной точки на противопо-

1			ложное вызывает изменение знака проекции кон-
1	dr	b
		b	сервативной силы F на направление перемеще-
			сервативной силы F на направление перемеще-
			ния, поэтому знак элементарной работы также из-
	F		меняется		Следовательно,
			меняется	A (Fdr ) .	Следовательно,

A1 b 2 A2 b 1 , поэтому работа консервативной силы вдоль замкнутой траектории 1–b–2–a–1 равна нулю:

A1 b 2 a 1 A1 b 2 A2 a 1 A2 b 1 A2 a 1 0 .

Точки 1 и 2, а также участки замкнутой траектории 1–a–2 и 2–b–1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы на произвольной замкнутой траектории L материальной точки равна нулю:

(Fdr ) 0 . В этой формуле кружок на знаке интеграла показывает, что инте-

грирование производится по замкнутому контуру L.

Пусть имеется консервативное силовое поле. Материальная точка (тело)
		расположена в точке N(x,y,z) этого поля.
N(x,y,z)		Выберем произвольную точку О этого поля
N(x,y,z)	Произвольная	(ее координаты x0,y0,z0), и назовем ее нача-
	Произвольная
	траектория
	траектория	лом отсчета потенциальной энергии. В точ-
		лом отсчета потенциальной энергии. В точ-
		ке О потенциальная энергия материальной
		точки равна нулю.
	O(x0,y0,z0)	Потенциальной энергией матери-
		альной точки в точке N консервативно-

го поля называется работа сил поля, совершаемая при перемещении материальной точки из точки N в точку О, принятую за начало отсчета потен-

O
циальной энергии: EП	(Fdr ) , где	F	– сила поля; интеграл вычисляется по

произвольной траектории между точками N и О.

Так как поле консервативное, то потенциальная энергия является только функцией координат x,y,z точки поля, в которой расположена материальная точка.

1		Если	материальная точка под	дей-
	2	ствием консервативных сил поля		пере-

		мещается	из произвольного начального

		положения 1 в произвольное конечное по-
		ложение 2, то работа этих сил равна убы-
	O	ли потенциальной энергии материальной
	O	точки: A1 2 EП1 ЕП 2 , где EП1 и EП 2 –
		точки: A1 2 EП1 ЕП 2 , где EП1 и EП 2 –

потенциальная энергия материальной точки в начальном и конечном положениях. Так как работа консервативных сил не зависит от формы траектории, то найдем работу консервативных сил по двум траекториям, одна из которых проходит через точку О – начало отсчета потенциальной энергии. Обозначим A1 2

– работа по траектории 1-2, A1 O 2 – работа по траектории 1–О–2. Так как поле консервативное, то A1 2 A1 O 2 .

Представим A1 O 2 как сумму работ на участках 1–О и О–2 по траектории

1–О–2, получим A1 2		A1 O 2	A1 O AO 2	A1 O A2 O .
Из определения		потенциальной энергии A1 O EП1,			A2 O EП 2 , тогда
A1 2 EП1 EП 2	(EП 2 EП1) EП . Элементарная работа консервативных
сил A dEП .	(6)
Уравнения A EП			и A dEП	определяют связь работы консер-

вативных сил с изменением потенциальной энергии поля (в интегральной и дифференциальной формах соответственно).

Итак, работа консервативной силы, определяется разностью потенциальной энергии тела в начальной и конечной точках пути. При элементарном перемещении работа равна минус изменению потенциальной энергии.


dA Fdr dEП .
Знак минус говорит о том, что работа совершается за счет убыли потенци-
альной энергии.
Работа консервативных сил на конечном участке пути 1 – 2:
2	EП 2 .
A12 Fdr EП 2 EП1 EП1	EП 2 .	(7)
1

Потенциальная энергия – функция, которая определяется с точностью некоторой произвольной постоянной, определяющей нулевой уровень потенциальной энергии. Так как в формулу работы консервативной силы входит только разность значений EП в двух положениях частицы, то нулевой уровень отсчета энергии выбирают произвольно. То есть потенциальную энергию тела в какомто определенном положении считают равной нулю. Энергию тела в других положениях отсчитывают относительно нулевого уровня. Тело, находящееся в

поле консервативных сил, обладает потенциальной энергией EП относительно нулевого уровня потенциальной энергии.

Конкретный вид функции EП зависит от характера силового поля.

Для определения потенциальной энергии тела (материальной точки) в консервативном силовом поле, необходимо выбрать положение начала отсчета нулевого уровня потенциальной энергии и вычислить работу силы при перемещении по произвольной траектории в этом поле из данной точки поля в точку отсчета нулевого уровня потенциальной энергии.

Пример 1: потенциальная энергия тела массы m, поднятого на высоту h над поверхностью Земли.

	z				Пусть материальная точка (тело) мас-
	z				сой m находится в точке N(x,y,z) однородно-
					сой m находится в точке N(x,y,z) однородно-
	z			N(x,y,z)	го поля силы тяжести. В качестве начала от-
		dr	α		счета потенциальной энергии выберем точ-
					счета потенциальной энергии выберем точ-

	h			mg	ку О начала декартовой системы координат.
				mg	ку О начала декартовой системы координат.
					Плоскость xOy	совместим с поверхностью
					Плоскость xOy	совместим с поверхностью
	O				Земли.
	O			x	Потенциальная энергия материальной
y	Нулевой уровень			x	Потенциальная энергия материальной
y	Нулевой уровень				точки (тела) в точке N поля равна работе си-
	потенциальной энергии				точки (тела) в точке N поля равна работе си-
					лы тяжести, совершаемой при перемещении
тела	из точки	N		с координатами x, y, z в		точку	O с координатами
x0 y0 z0 0.				Тогда	элементарная		работа	равна:
			cos mgdz , где dz dr cos .
A mgdr mg dr			cos mgdz , где dz dr cos .

При перемещении тела из точки N в точку О работа силы тяжести равна:

A mgdz mg(0 z) mgz mgh .

Работа силы тяжести при падении тела на Землю равна потенциальной энергии

EП mgh ,

если за нуль принята потенциальная энергия тела, лежащего на Земле.

Пример 2: потенциальная энергия тела массой m, находящегося в точке N

на расстоянии r от тела массой M. Тело массой M

является источником грави-

тационного поля.

За

начало

отсчета

потенциальной

энергии выберем точку О (на бесконечно

большом удалении

rO от тела массой

Fгр

M). Потенциальная энергия материальной

точки (тела) в точке N равна работе АNO

гравитационной силы, совершаемой при

перемещении тела из точки N в точку O по

произвольной траектории.

Вычислим работу гравитационной силы:

dr Mm (

)

(Fгрdr )

r 2

Как следует из полученного выражения, если начало отсчета потенциаль-

ной энергии – точка О – выбрано «в бесконечности» ( rO ), то потенциальная

энергия тела (материальной точки) во всех точках пространства вокруг тела

массой М отрицательна.

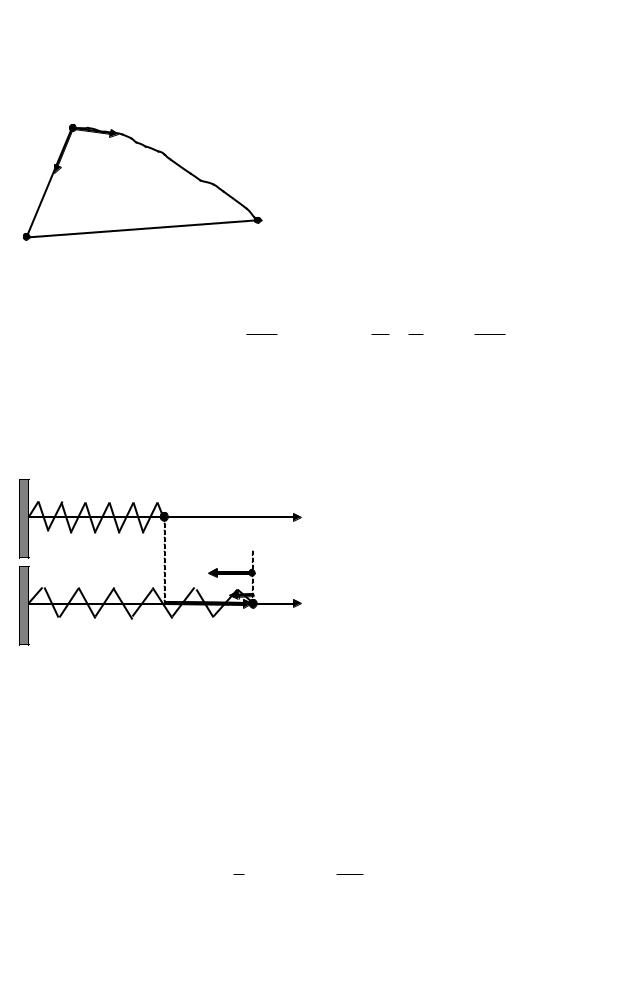
Пример

потенциальная

Fупр 0

энергия

упруго

деформированной

пружины.

Рассмотрим пружину, один ко-

Fупр kr

нец которой закреплен, а другой

может перемещаться горизонтально

под

действием

внешней

силы.

Направим координатную ось x па-

раллельно оси пружины и выберем

начало отсчета координаты x (x0 = 0)

в положении незакрепленного конца недеформированной пружины (точка О).

Когда пружина не деформирована, тело (материальная точка) массой m

находится в точке с координатой x = 0. Примем точку О за начало отсчета по-

тенциальной энергии.

Потенциальная энергия материальной точки (тела массой m) в произволь-

ном положении N с координатой x равна работе АNO упругой силы, совершае-

мой при перемещении тела из точки N в точку О.

Вычислим работу упругой силы при перемещении тела из точки N в точку

x0 0

kxdx

(x2 x02 )

О:

A ( krdr )

Как следует из полученного выражения, материальная точка, находящаяся

на

конце

деформированной

пружины

обладает

потенциальной

энергией

1 / 21 2 > Следующая >>>

Соседние файлы в папке РАЗДЕЛ №1. МЕХАНИКА

#
27.11.20247.79 Mб43 ВЫБИВАНИЕ ПЛАСТИНКИ, ВЫДЕРГИВАНИЕ СКАТЕРТИ.mp4
#
27.11.2024490.13 Кб43 Конспект лекции на тему ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ.pdf
#
27.11.20241.05 Mб43 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ НА ТЕМУ ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ.pdf
#
27.11.2024343.04 Кб43 Презентация лекции по теме ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ.ppt
#
27.11.2024619.38 Кб44 Конспект лекции на тему РАБОТА И ЭНЕРГИЯ.pdf
#
27.11.2024844.36 Кб44 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ НА ТЕМУ РАБОТА И ЭНЕРГИЯ.pdf
#
27.11.2024347.14 Кб44 Презентация по теме РАБОТА И ЭНЕРГИЯ.ppt
#
27.11.2024425.25 Кб45 Конспект лекции на тему ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.pdf
#
27.11.2024800.26 Кб55 Презентация лекции по теме ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.ppt
#
27.11.2024738.61 Кб86 Конспект лекции на тему ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ.pdf
#
27.11.202468.64 Mб46 МАЯТНИК МАКСВЕЛЛА.mp4