Лабораторная работа 1.2 Криптоанализ шифров табличной перестановки
Описание задания
В шифрах табличной перестановки криптограмма (зашифрованный текст) может быть получена разными способами. Для открытого текста длиной N подбирается таблица размером mхn, m∙n≥ N, символы текста записываются в ячейки таблицы. Запись может производиться как построчно, так и в столбец. В простейшем варианте текст из таблицы считывается в направлении, отличном от записи (например, по столбцам, если записывался по строкам).
Для усиления шифра перед считыванием текста из таблицы возможны перестановка столбцов/строк таблицы либо совместная перестановка строк и столбцов (двойная перестановка). Порядок считывания текста в этом случае может и не меняться.
Пусть текст записывается в таблицу построчно, затем производится перестановка столбцов таблицы, текст из таблицы считывается также построчно. Ключом такого шифра будет размер шифрующей таблицы и порядок следования ее столбцов.
При решении задачи криптоанализа необходимо восстановить начальный порядок следования букв текста. Таким образом, необходимо произвести действия, обратные шифрованию.
Для выяснения правильного порядка следования столбцов может быть использован частотный анализ буквосочетаний. Например, для русского языка характерно чередование гласных и согласных букв: после гласной чаще встречается согласная, а после согласной — гласная буква. Таблицы сочетаемости букв русского языка, чередования гласных и согласных, частотные таблицы биграмм можно найти в литературе.
Знание частот встречаемости пар букв (биграмм) позволяет легко вскрывать шифры табличной перестановки. Истинный порядок следования столбцов/строк в таблице можно восстановить, рассматривая и исключая маловероятные сочетания бук в. Кроме того, на основе вероятностей появления биграмм можно рассчитать вероятность следования одного столбца (строки) шифрующей таблицы за другим.
Чтобы оценить вероятность p(i,j) следования столбца j непосредственно за столбцом i, надо для каждой строки рассмотреть сочетания символов из этих столбцов. Получим m вероятностей p(eki, екj) биграмм, где m — число строк шифрующей таблицы; eki, екj — символы, стоящие в шифрующей таблице на пересечении строки k и столбца i,j соответственно. Окончательно получим
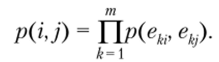
Пользуясь этой формулой, можно вычислить вероятности следования друг за другом всех возможных пар столбцов p(i,j), i ≠ j: i,j = 1,..., n, n — число столбцов шифрующей таблицы. Если в исходном тексте столбец j действительно стоит после i-го, то вероятность p(i,j) должна быть, в принципе, больше вероятностей p(i, k), k≠j и p(k,j), k ≠ i. Руководствуясь этими соображениями, для таблиц небольшого размера несложно восстановить истинный порядок следования столбцов.
Предположим теперь, что в шифрующей таблице была произведена перестановка не только столбцов, но и строк. Ключом такого шифра будет размер шифрующей таблицы, порядок следования ее столбцов и строк. Тогда при дешифровании следует сначала восстановить исходный порядок следования столбцов. Получив фрагменты связного текста внутри каждой строки, можно восстановить порядок следования самих строк.
Задание
Дешифровать криптограммы, полученные методом столбцовой и двойной перестановки. Известно, что запись и считывание текста осуществляется построчно, пробелы в тексте сохранены и обозначены знаком подчеркивания. Численные оценки возможности взаимного следования столбцов шифрующей таблицы считаются известными (заданы).
Технология выполнения задания
Задание 1. Дешифровать криптограмму, полученную шифром столбцовой перестановки.