
3к5с Архитектура информационных систем / Архитектура информационных систем / МУ 2 Архт ИС
.docxПрактическая работа по дисциплине «Архитектура ЭВМ»
Работа и особенности логических элементов ЭВМ.
Цель работы: Освоить работу логических элементов.
ОСНОВНЫЕ ПОНЯТИЯ
Диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна - наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств. Количество пересечений (областей) n определяется по формуле:
n=2N,
где N - количество множеств.
Таким образом, если в задаче используется два множества, то n=2*2=4, если три множества, то n=2*3=8, если четыре множества, то n=2*4=16. Поэтому диаграммы Эйлера-Венна используются в основном для двух или трех множеств.
Множества изображаются в виде кругов (если используется 2-3 множества) и эллипсов (если используется 4 множества), помещенных в прямоугольник (универсум).
Универсальное множество (универсум) U (в контексте задачи) - множество, содержащее все элементы рассматриваемой задачи: элементы всех множеств задачи и элементы, не входящие в них.
Пустое множество Ø (в контексте задачи) - множество, не содержащее ни одного элемента рассматриваемой задачи.
На диаграмме строят пересекающиеся множества, заключают их в универсум. Выделяют области, количество которых равно количеству пересечений.
Диаграммы Эйлера-Венна также используются для визуального представления логических операций.
2. Законы алгебры логики
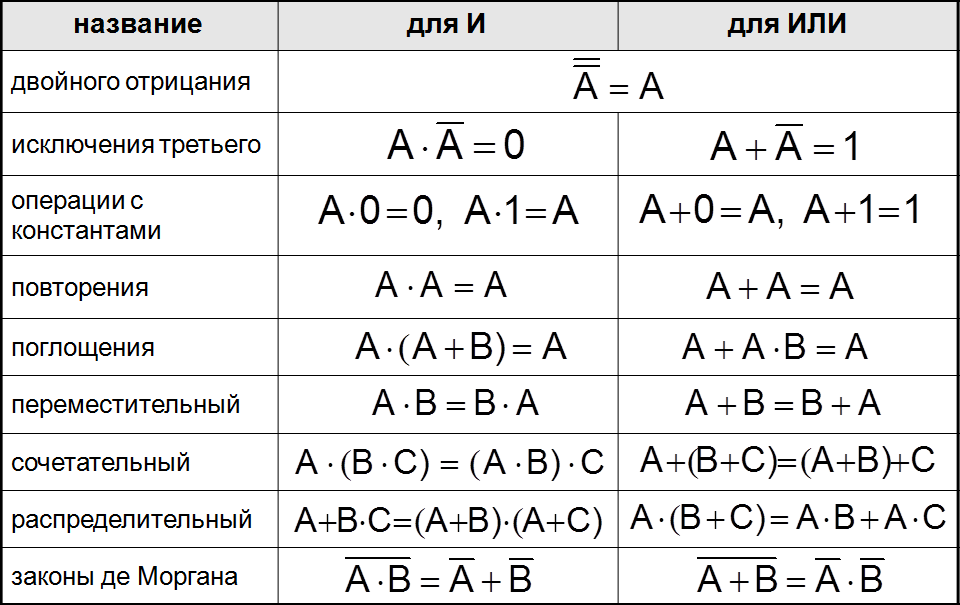
Логические выражения можно преобразовывать в соответствии с законами алгебры логики:
2.1 Законы рефлексивности
a ∨ a = a
a ∧ a = a
2.2 Законы коммутативности
a ∨ b = b ∨ a
a ∧ b = b ∧ a
2.3 Законы ассоциативности
(a ∧ b) ∧ c = a ∧ (b ∧ c)
(a ∨ b) ∨ c = a ∨ (b ∨ c)
2.4 Законы дистрибутивности
a ∧ (b ∨ c) = a ∧ b ∨ a ∧ c
a ∨ b ∧ c = (a ∨ b) ∧ (a ∨ c)
2.5. Закон отрицания отрицания
¬ (¬ a) = a
2.6 Законы де Моргана
¬ (a ∧ b) = ¬ a ∨ ¬ b
¬ (a ∨ b) = ¬ a ∧ ¬ b
2.7 Законы поглощения
a ∨ a ∧ b = a
a ∧ (a ∨ b) = a
2.8 Закон исключающее «или» (сложение по модулю 2)
ab = (¬xy)∨(x¬y)
3. Таблицы истинности
3.1 Операция «И»

3.2 Операция «ИЛИ»
3.3. Операция «исключающее или»
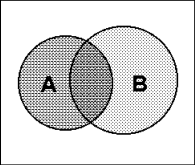
4. Диаграммы Эйлера-Венна

Конъюнкция (логическое умножение «И»)
A & B
A and B
A * B
A /\ B

Дизъюнкция (логическое сложение «ИЛИ»)
A \/ B
A or B
A || B
A | B
ТЕХНОЛОГИЯ РАБОТЫ
Рассмотрите пример построения диаграмм Эйлера-Венна для двух и трех множеств.
Пример 1
Пусть есть следующие множества чисел:
А={1,2,3,4}
В={3,4,5,6}
Универсум U={0,1,2,3,4,5,6}
Диаграммы Эйлера-Венна для двух множеств А и В:
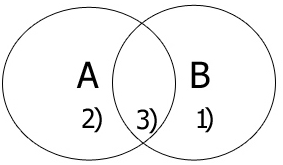
Определим области, и числа которые им принадлежат:
А |
B |
Обозначение области |
Числа |
0 |
0 |
0) |
0 |
0 |
1 |
1) |
5,6 |
1 |
0 |
2) |
1,2 |
1 |
1 |
3) |
3,4 |
Задание:
Изобразить выражения согласно варианту (таблица 1) на диаграммах Эйлера.
Описать логическим выражением диаграмму Эйлера согласно варианту (таблица 2).
Таблица 1.
-
Вариант
Выражения
1
А˅(В&С)
А-(В˅
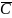 )
)2
А
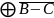
А˅
 ˅С
˅С3
А&

А˅В-С
4
А˅В
 С
С ˅(В&С)
˅(В&С)5

А˅(
 )
)6
А&В-С
А
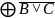
7
А В˅
А-(В&С)
8

(А-В)˅С
9
А-В-С

10
А-(В&С)
 С
С11
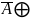 В˅С
В˅СА-
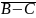
12
А&В&С
 -С
-С13
А В С

14
(А В)˅

15
&В-
А (В˅С)
Таблица 2.
-
Вариант
Выражения
1

2
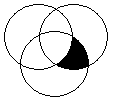
3
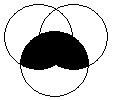
4
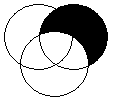
5
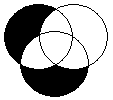
6

7

8
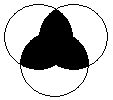
9

10

11
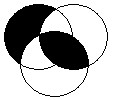
12

13
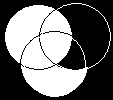
14

15
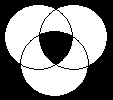
ТРЕБОВАНИЯ БЕЗОПАСНОСТИ ТРУДА
При выполнении практической работы необходимо соблюдать общие правила техники безопасности:
использовать ПК только в соответствии с их назначением;
не размещать на корпусе ПК посторонние предметы (тетради, книги, карандаши и т.п.);
оберегать ПК от толчков, ударов, сотрясений;
немедленно поставить в известность оператора ИВЦ об обнаружении задымления, загорания, пожара;
немедленно сообщить оператору ИВЦ обо всех неисправностях в работе ПК.
СОДЕРЖАНИЕ ОТЧЕТА
Отчёт по практической работе на листах формата А4, который должен содержать: цель работы и выполненные задания по практической работе.
