СОДЕРЖАНИЕ

ЗАДАНИЕ 1 2

ЗАДАНИЕ 2 5

ЗАДАНИЕ 1

Требуется построить эффективный код сообщения с помощью метода Шеннона-Фано и метода Хаффмана. Найти оптимальную длину символа передаваемого сообщения.

Сообщение, передаваемое по каналу связи, состоит из 8 символов, которые имеют следующую вероятность: А - 0.005, Б - 0.1, В - 0.725, Г - 0.031, Д - 0.005, Е - 0.071, Ж - 0.03, З - 0.033.

Чтобы закодировать по методу Шеннона-Фано сообщение, надо записать символы по убыванию вероятности появления каждого символа. Данные занесем в таблицу:

Сообщение	В	Б	Е	З	Г	Ж	А	Д
Вероятность	0,725	0,1	0,071	0,033	0,031	0,03	0,005	0,005

Построение кодового дерева начинают с вершины, листья которого представляют собой кодируемые сообщения с присвоенными им кодовыми словами. Выполним построение, занесем коды и сообщения в таблицу:

Коды	Сообщения
0	В
11	Б
101	Е
1001	З
10001	Г
100000	Ж
1000010 1000011	A Д

Цена кодирования (средняя длина кодового слова) является критерием степени оптимальности кодирования. По формуле вычислим ее в нашем случае:

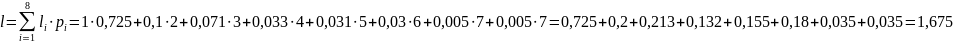
Закодируем сообщение из предыдущего примера по методу Хаффмана.

Для того, чтобы закодировать сообщения по Хаффману, предварительно преобразуется таблица, задающая вероятности сообщений. Исходные данные записываются в столбец, две последние (наименьшие) вероятности в котором складываются, а полученная сумма становится новым элементом таблицы, занимающим соответствующее место в списке убывающих по величине вероятностей. Эта процедура продолжается до тех пор, пока в столбце не останутся всего два элемента. Построим таблицу:

Сообщения	P	P1	P2	P3	P4	P5	P6
В	0,725 0,1 0,071 0,033 0,031 0,03 0,005 0,005	0,725 0,1 0,071 0,033 0,031 0,03 0,01	0,725 0,1 0,071 0,033 0,031 0,04	0,725 0,1 0,071 0,033 0,071	0,725 0,1 0,071 0,104	0,725 0,1 0,175	0,725 0,275
Б
Е
З
Г
Ж
A
Д

Построение кодового дерева начинается с корня. Это продолжается до тех пор, пока в таблице остаются вероятности, получившиеся в результате суммирования. Построение кодового дерева заканчивается образованием листьев, соответствующих данным сообщениям с присвоенными им кодами. Занесем данные в таблицу и построим дерево, полученное в результате кодирования по Хаффману:

Коды	Сообщения
0	В
11	Б
101	Е
1001	З
10001	Г
100000	Ж
1000010 1000011	A Д

Цена кодирования здесь будет равна:

ЗАДАНИЕ 2

Используя алгоритм помехоустойчивого кодирования информации Хемминга, получить кодовую комбинацию для числа А. Предварительно перевести его в двоичную систему счисления. Осуществить декодирование числа В (варианты заданий даны в табл. 3). Сделать вывод о достоверности передачи (о наличии ошибки в принятой комбинации).

Переведем число А=20 в двоичную систему счисления: А=10100.

Рассмотрим код Хемминга, исправляющий все одиночные ошибки. В качестве исходного берем двоичный код на все сочетания с числом информационных символов k, к которому прибавляем контрольные символы m. Таким образом, общая длина закодированной комбинации: n = k+ m. Этапы кодирования по Хеммингу.

Определение числа контрольных символов. При передаче по каналу с шумами может быть искажен любой из n символов кода или слово передано без искажений. С помощью контрольных символов m можно описать оба события. Значит должно быть выполнено условие: 2m>n+1 = (k+m)+1. Размещение контрольных символов. Так как произвольное расположение контрольных символов затрудняет проверку принятого кода, то для удобства обнаружения искаженного символа целесообразно размещать их на местах, кратных степени 2 (1,2,4,8 и т.д.). Поэтому при k=5, m=4 закодированная комбинация будет выглядеть так: m1, m2, к5, m3, k4, k2, m4, k1. Определение состава контрольных символов. С помощью проверки на четность выявляют, какой из символов должен стоять на позиции "1" или "0". Рассмотрим это на примере комбинации.

1	2	3	4	5	6	7	8	9
M1	M2	K5	M3	K4	K3	K2	M4	K1
1	0	1	1	0	1	0	0	0
1	0	1	0	1	0	1	0	1	M1	1
0	1	1	0	0	1	1	0	0	M2	0
0	0	0	1	1	1	1	0	0	M3	1
0	0	0	0	0	0	0	1	1	M4	0

Контрольные символы имеют значение 1010, следовательно, переданная комбинация имеет вид 101101000.

Декодирование. Для проверки правильности принятых комбинаций снова используем метод проверки на четность. Если комбинация принята без искажений, то сумма по модулю 2 всех её разрядов дает 0. При искажении какого-либо символа суммирование при проверке может дать единицу. По результатам суммирования каждой из проверок составляется двоичное число, указывающее на место искажения. Результатом корректирующего декодирования будет кодовая комбинация, состоящая из 4-х символов (без проверочных). Составим таблицу:

1	2	3	4	5	6	7	8	9
M1	M2	K5	M3	K4	K3	K2	M4	K1
1	0	1	1	0	1	1	1	1
1	0	1	0	1	0	1	0	1	M1	0
0	1	1	0	0	1	1	0	0	M2	1
0	0	0	1	1	1	1	0	0	M3	1
0	0	0	0	0	0	0	1	1	M4	0

Вычисляем все контрольные биты. Для этого обнуляем все биты, находящиеся на номерах степеней двойки:

Полученный код 0110 = 6

Номер контрольного бита 6, в котором присутствует ошибка. Меняем шестой бит на обратный - с единицы на ноль и получаем исходное сообщение: 10011