Балаковский инженерно-технологический институт – филиал

федерального государственного автономного образовательного учреждения

высшего образования

«Национальный исследовательский ядерный университет «МИФИ»

Факультет атомной энергетики и технологий

Кафедра «Информатика и управление в технических системах»

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

«Моделирование процессов и систем»

Выполнил: студент группы ИФСТ 4 з/у

Сейфетдинов Руслан Халимович

«_____»______________201___г.

Проверила доцент Фролова М.А. «_____»______________201__г.

СОДЕРЖАНИЕ

ЗАДАНИЕ №1 3

ЗАДАНИЕ №2 5

ЗАДАНИЕ №4 11

ЗАДАНИЕ №5 14

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ 16

ЗАДАНИЕ №1

Определить основные показатели функционирования одноканальной СМО «Станок – изделие» (рисунок 1). Входной поток является простейшим со средним временем между поступлением заявок 120 минут и временем обработки – 72 минут. Выполнить задания используя MS Excel.

Рисунок 1 – Одноканальная СМО

Основные данные:

t_p = 120 минут

t_обсл =72 минуты

λ – интенсивность потока требований (число требований за еди­ницу времени):

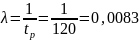
t_p – среднее время между поступлением заявок.

Интенсивность обслуживания:

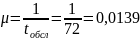
t_обсл – время обслуживания одного требования

Определим показатели качества СМО с одним устройством обслуживания:

1. Коэффициент загрузки устройства:

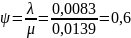
2. Вероятность простоя канала обслуживания:

3. Вероятность того, что в системе находится m требований:

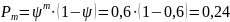
4. Среднее число обслуживаемых требований, находящихся в системе:

5. Среднее число требований, находящихся в очереди:

6. Среднее время ожидания требований:

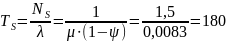
ЗАДАНИЕ №2

СМО имеет 5 устройств, работающих в 1 смену. Поток клиентов простейший с интенсивностью 14 клиентов в час. Время обслуживания показательное со средним временем t_обсл = 20 минут. Определить показатели качества обслуживания.

Рассмотрим многоканальную СМО (рисунок 2). Число каналов в СМО обозначается n.

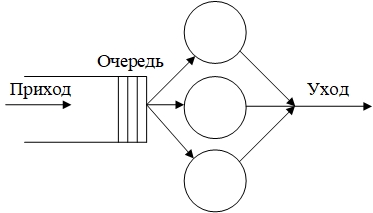
Рисунок 2 – Многоканальная система массового обслуживания

Исходные данные:

Число устройств – 5

Интенсивность потока за час – 14

Время обслуживания – 20 минут

Порядок вычислений:

Определим показатели качества многоканальной СМО

1. Интенсивность входного потока:

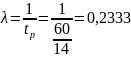
где t_p – среднее время между поступлением заявок

2. Интенсивность обслуживания:

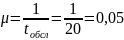
где t_обсл – время обслуживания одного требования

3. Коэффициент загрузки устройства:

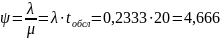
4. Вероятность того, что все обслуживающие системы свободны

5. Вероятность того, что все обслуживающие устройства заняты

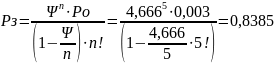
6. Среднее число устройств, свободных от обслуживания:

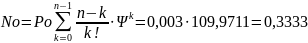
7. Коэффициент простоя обслуживающих устройств:

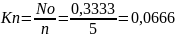
8. Среднее число устройств, занятых обслуживанием:

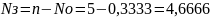
9. Коэффициент загрузки системы:

10. Средняя длина очереди:

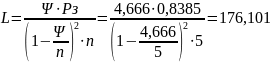
11. Среднее время ожидания требований в очереди:

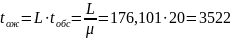
Итог вычислений представлен на рисунке 3.

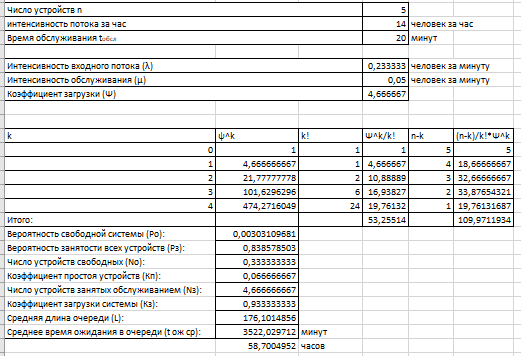
Рисунок 3 – Итог вычисления задачи №2

Выполним вычисления для 8 устройств. Результат вычислений представлен на рисунке 4.

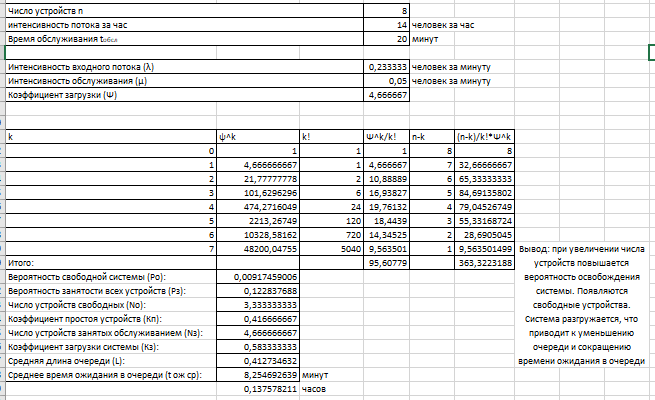
Рисунок 4 – Итог вычисления задачи №2 с 8 устройствами

Вывод: при увеличении числа устройств повышается вероятность освобождения системы. Появляются свободные устройства. Система разгружается, что приводит к уменьшению очереди и сокращению времени ожидания в очереди

ЗАДАНИЕ №3

СМО имеет 12 устройств, работающих в 1 смену. Поток клиентов простейший с интенсивностью 48 клиентов в час. Время обслуживания показательное со средним временем t_обсл = 24 минуты. Определить показатели качества обслуживания.

Рассмотрим многоканальную СМО (рисунок 5). Число каналов в СМО обозначается n.

Рисунок 5 – Многоканальная система массового обслуживания

Исходные данные:

Число устройств – 12

Интенсивность потока за час – 48

Время обслуживания – 24 минут

Порядок вычислений

Определим показатели качества многоканальной СМО

1. Интенсивность входного потока:

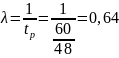
где t_p – среднее время между поступлением заявок

2. Интенсивность обслуживания:

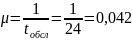
где t_обсл – время обслуживания одного требования

3. Коэффициент загрузки устройства:

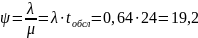
4. Вероятность того, что все обслуживающие системы свободны

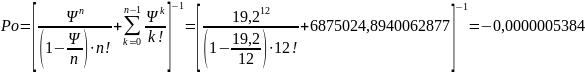
5. Вероятность того, что все обслуживающие устройства заняты

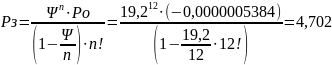
6. Среднее число устройств, свободных от обслуживания:

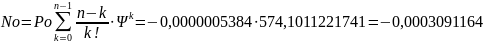
7. Коэффициент простоя обслуживающих устройств:

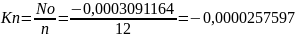
8. Среднее число устройств, занятых обслуживанием:

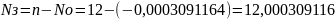
9. Коэффициент загрузки системы:

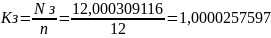
10. Средняя длина очереди:

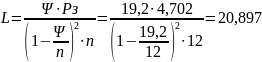
11. Среднее время ожидания требований в очереди:

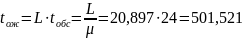
Итог вычислений представлен на рисунке 6.

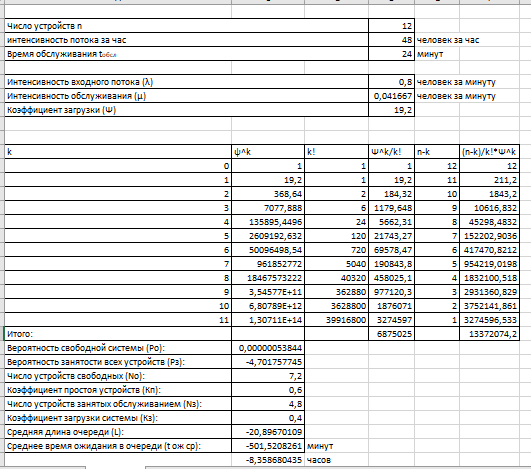
Рисунок 6 – Вычисления показателей качества десятиканальной СМО

ЗАДАНИЕ №4

Среднее время обслуживания в многоканальной СМО составляет 12 минут, интенсивность поступления заявок = 96 заявок за день (8 часов). Определить количество каналов в СМО и показатели качества СМО.

Рассмотрим многоканальную СМО (рисунок 7). Число каналов в СМО обозначается n.

Рисунок 7 – Многоканальная система массового обслуживания

Исходные данные:

Число устройств - 3

Интенсивность заявок за день (8 часов) – 96

Интенсивность заявок за час 12

Время обслуживания – 12 минут

Порядок вычислений

Определим показатели качества многоканальной СМО

1. Интенсивность входного потока:

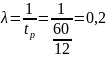
где t_p – среднее время между поступлением заявок

2. Интенсивность обслуживания:

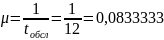
где t_обсл – время обслуживания одного требования

3. Коэффициент загрузки устройства:

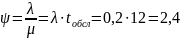
3.1 Согласно формулы: 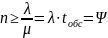, определяем, что количество каналов n = 3.

4. Вероятность того, что все обслуживающие системы свободны

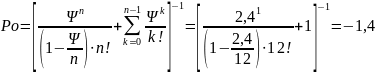
5. Вероятность того, что все обслуживающие устройства заняты

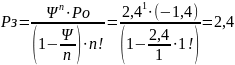
6. Среднее число устройств, свободных от обслуживания:

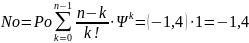
7. Коэффициент простоя обслуживающих устройств:

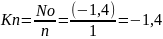
8. Среднее число устройств, занятых обслуживанием:

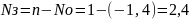
9. Коэффициент загрузки системы:

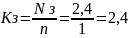
10. Средняя длина очереди:

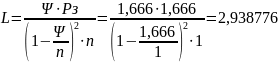
11. Среднее время ожидания требований в очереди:

Итог вычислений представлен на рисунке 8.

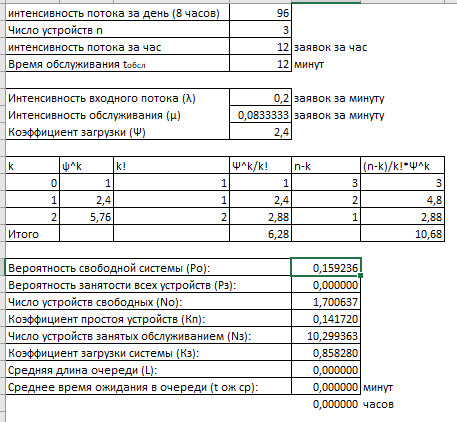
Рисунок 8 – Показатели качества одноканальной СМО

ЗАДАНИЕ №5

Рассчитать по диаграмме работы многоканальной СМО оценки характеристик работы СМО. Рассмотрим диаграмму работы многоканальной СМО с двумя устройствами (ПР 1 и ПР 2) и двумя позициями для ожидания в очереди (Поз. 1 и Поз. 2) – рисунок 9.

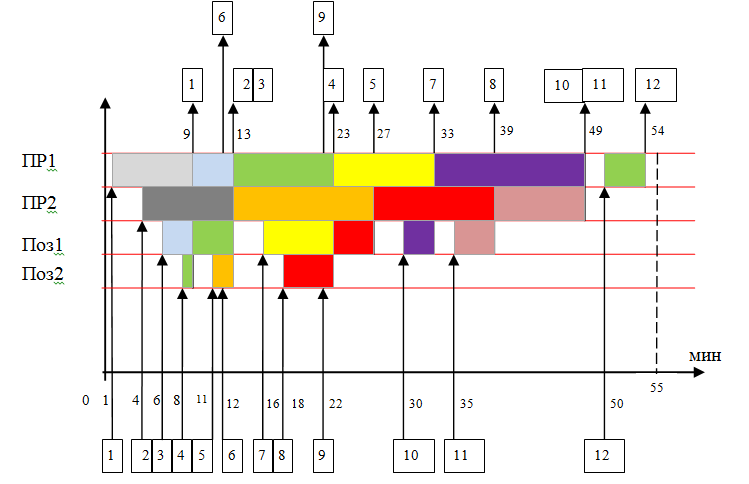
Рисунок 9 – Диаграмма работы многоканальной СМО

Время наблюдения за СМО (Т_H) составляет 55 мин.

Рассчитаем по диаграмме некоторые оценки характеристик работы СМО.

1. Вероятность обслуживания требования

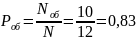
где N_oб, N- количество обслуженных требований и общее количество требований, соответственно.

2. Пропускная способность СМО в требованиях в минуту

.

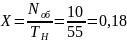3. Вероятность отказа в обслуживании

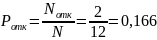
где N_отк - количество требований, которым отказано в обслуживании.

4. Вероятность того, что требование застанет оба устройства свободными,

где T_св - время, на протяжении которого оба устройства были свобод­ными (определяем по диаграмме).

5. Вероятность того, что обслуживанием занято только одно устройство из двух,

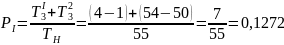
где Т¹₃, Т²₃ - время, когда было занято только первое и только второе устройство, соответственно.

6. Вероятность того, что обслуживанием заняты оба устройства,

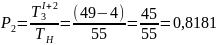
где T¹⁺²₃ - время, когда были занятые оба устройства.

7. Среднее количество занятых устройств

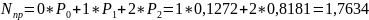
8. Вероятность того, что в очереди нет требований,

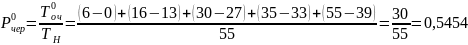
где T⁰_оч - время, на протяжении которого в очереди не было требований.

9. Вероятность того, что в очереди есть только одно требование,

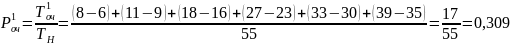
где T¹_оч - время, когда в очереди было только одно требование.

10. Вероятность того, что в очереди два требования,

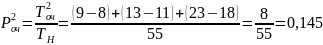
где Т²_оч - время, на протяжении которого в очереди было два требо­вания.

11. Среднее количество требований в очереди

12. Среднее время пребывания в очереди

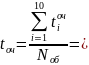
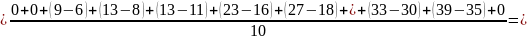
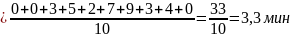
где t_i^оч - время пребывания i -го требования в очереди (j = 1,2,...).

13. Среднее время пребывания в очереди без учета требований, которые не ждали,

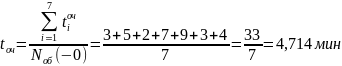
где N_об(-О) - количество требований, которые не ждали в очереди.

14. Среднее время обслуживания требования в устройствах

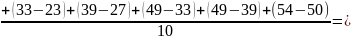
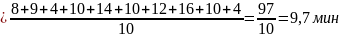
где t_i^об - время обслуживания i -го требования в СМО (i = 1,2,...).

15. Общее среднее время пребывания требования в СМО

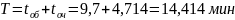
16. Среднее количество требований в системе обслуживания

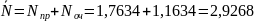
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Алпатов, Ю.Н. Моделирование процессов и систем управления: учебное пособие / Ю.Н. Алпатов. — Санкт-Петербург: Лань, 2018. — 140 с.

2. Рыжиков, Ю.И. Имитационное моделирование. Авторская имитация систем и сетей с очередями: учебное пособие / Ю.И. Рыжиков. — Санкт-Петербург: Лань, 2019. — 112 с.

3. Бурнаева, Э.Г. Обработка и представление данных в MS Excel: учебное пособие / Э.Г. Бурнаева, С.Н. Леора. — Санкт-Петербург: Лань, 2018. — 156 с.

Балаково 2019