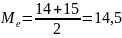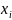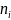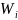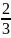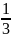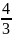2к4с Теория вероятностей и математическая статистика / КР / КР-Вариант №8 (Сейфетдинов Р.Х.)
.docxЗадание 1
Имеется 9 лотерейных билетов, среди которых 2 выигрышных. Найти вероятность того, что среди 4 наудачу купленных билетов нет выигрышных.
Решение:
Обозначим событие A – среди 4 наудачу купленных билетов нет выигрышных
По
классическому определению вероятности:
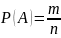
Можно купить любые 4 билета из 9. Общее количество исходов найдем по формуле сочетаний из 9 по 4:
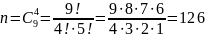
Всего билетов без выигрыша 9-2=7
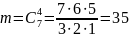
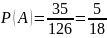
Ответ:
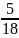
Задание 2
В торговом центре два одинаковых автомата продают шоколадки. Вероятность того, что к концу дня в первом автомате закончатся шоколадки, равна 0,4. Вероятность того, что шоколадки закончатся во втором автомате, равна 0,14. Найдите вероятность того, что к концу дня шоколадки останутся в обоих автоматах.
Решение:
A – к концу дня шоколадки остануться в обоих автоматах;
А1 – к концу дня в 1 автомате шоколадки останутся;
А2 – к концу дня в 1 автомате шоколадки останутся.
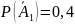
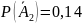
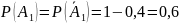
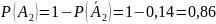
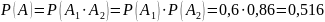
Ответ: 0,516
Задание 3
В спартакиаде участвуют из первой группы 9 студентов, из второй – 6. Студент из первой группы попадает в сборную института с вероятность 0,9, второй – 0,7. Наудачу выбранный студент попал в сборную. Какова вероятность того, что это студент из второй группы?
Решение:
Обозначим события:
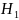– выбранный
студент из 1 группы;
– выбранный
студент из 2 группы;
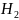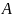– выбранный
студент попадет в сборную.
Всего
участников:
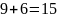
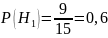
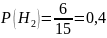
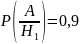
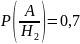
По формуле полной вероятности:
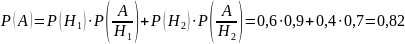
По формуле Бейеса:
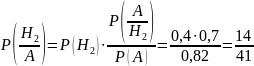
Ответ: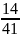
Задание 4
Вероятность того, что поезд прибудет на станцию с отклонением от графика, равна 0,2. Найти вероятность того, что из 400 случайно отобранных поездов от 70 до 80 прибудут не по графику.
Решение:
Событие – поезд прибудет на станцию с отклонением от графика
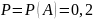
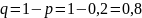
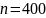
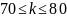
По интегральной теореме Муавра-Лапласа:
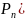
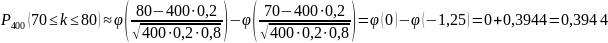
Ответ:
Задание 5
Найти числовые характеристики непрерывной случайной величины, заданной плотностью распределения 𝑓(𝑥) = х⁄2 в интервале 0,2.
Решение:
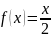при
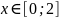
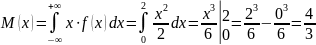
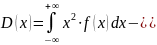
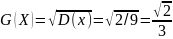
Ответ:
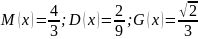
Задание 6
В таблице представлены данные о возрасте обучающихся (полных лет) на курсах иностранного языка. Построить статистический ряд частот и частостей, полигон относительных частот. Найти числовые характеристики выборки.
4 |
13 |
13 |
15 |
16 |
17 |
9 |
20 |
19 |
7 |
23 |
23 |
23 |
9 |
22 |
23 |
14 |
4 |
20 |
20 |
12 |
18 |
15 |
10 |
10 |
13 |
14 |
5 |
6 |
17 |
Решение:
Статический ряд частот:
|
4 |
5 |
6 |
7 |
9 |
10 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
22 |
23 |
|
2 |
1 |
1 |
1 |
2 |
2 |
1 |
3 |
2 |
2 |
1 |
2 |
1 |
1 |
3 |
1 |
4 |
Объем выборки:
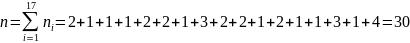
Построим статистический ряд частостей
|
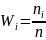
4 |
5 |
6 |
7 |
9 |
10 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
22 |
23 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
Построим полигон относительных частот:
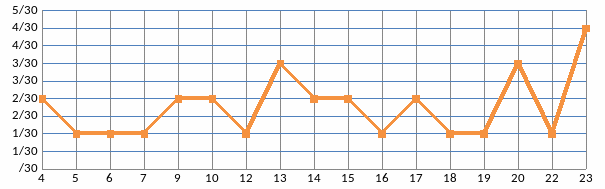
Найдем числовые характеристики выборки.
Выборочное среднее:
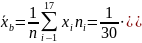
Выборочная дисперсия:
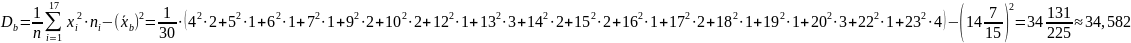
Выборочное среднеквадратическое отклонение
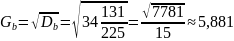
Исправленная выборочная дисперсия:
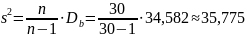
Исправленное среднеквадратическое отклонение:
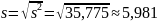
Мода: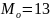
и
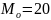
Медиана:
