19. Определение случайной величины, дискретной и непрерывной случайной величины.

В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.

20. Закон распределения вероятностей дсв.

Закон распределения вероятностей ДСВ Для того чтобы ДСВ была задана, не достаточно перечислить множество ее всевозможных значений, потому что две ДСВ могут иметь одинаковый перечень возможных значений, а вероятности принятия этих значений будут различными. О. 1. Законом распределения вероятностей (рядом распределения) ДСВ называется последовательность возможных значений дискретной случайной величины и соответствующих им вероятностей. Закон распределения вероятностей может быть задан: 1) Таблично, при этом первая строка в таблице содержит возможные значения ДСВ, а вторая – их вероятности:

X	x1	x2	xn
P	p1	p.	pn

2) Графически, для чего в прямоугольной системе координат строят точки  , а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

3) Аналитически, т.е. в виде формулы. Наиболее распространенными аналитическими выражениями являются биномиальное, пуассоновское, геометрическое и гипергеометрическое распределения вероятностей. Т. к. в одном испытании ДСВ может принять только одно значение, то множество ее всевозможных значений образует полную группу событий и сумма их вероятностей равна единице: . 2. Способы задания. 1. Биномиальное распределение 2. Пуассоновское распределение 3. Геометрическое распределение 4. Гипергеометрическое распределение

21. Табличное задания закона распределения дсв.

22. Графическое задание закона распределения дсв.

23. Определение математического ожидания дсв.

24. Свойства математического ожидания дсв.

1. Математическое ожидание постоянной величины равно этой постоянной:

М(С) = С.

2. Постоянный множитель можно выносить за знак математического ожидания:

М(СХ) = СМ(Х),

гдеС — постоянная.

3. Математическое ожидание алгебраической суммы конечного числа п случайных величин равно алгебраической сумме их математических ожиданий:

М(Х₁ ± Х₂ ±…± Х_п) = М(Х₁)±М(Х₂) ±…±М(Х_п).

4. Математическое ожидание произведения конечного числа п независимых случайных величин равно произведении¹ их математических ожиданий:

М(Х₁•Х₂•…•Х_п) = М(Х₁) •М(Х₂) •…•М(Х_п).

 

5. Если все значения случайной величины X уменьшить (увеличить) на одно и то же число с, то ее математическое ожидание уменьшится (увеличится) на то же число с:

М(Х ± С) = М(Х) ± М(С) = М(Х) ± С.

Следствие. Математическое ожидание отклонения значе­ний случайной величины X от ее математического ожида­ния равно нулю:

М[Х- М(Х)] = 0.

25. Определение дисперсии дсв.

Опр. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

Теорема: Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания данной случайной величины

26. Формула для вычисления дисперсии.

27. Свойства дисперсии дсв.

Дисперсия постоянной величины равна нулю.

Д(С) – М(С- М(С))2 = М(С - С) 2 = М(0) 2 = 0

Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат

Д(СХ) = С2 Д(Х)

Доказательство:

Д(СХ) = М(СХ – М(СХ))2 = М(СХ – СМ(Х))2 = М(С(Х – М(Х)))2 =

С2М(Х – М(Х))2 = С2 Д(Х)

Дисперсия суммы нескольких взаимно-независимых случайных величин равна сумме дисперсий этих величин

Д(Х1 ± Х2 ± … ± Хn) = Д(Х1)+ Д(X2) + … Д(Хn),

где Х1, Х2, … Хn – взаимно-незасвисимые величины.

Следствие: дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины

Д(С + Х) = Д(Х)

Д(С+ Х) = Д(С+ Х)=Д(С) + Д(Х) = Д(Х)

Постоянная не дает рассеяние ее прибавление к случайной величине Х ведет лишь к смещению всех ее значений на одну и ту же постоянную величину, а рассеяние остается прежним.

28. Среднее квадратическое отклонение.

Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение ( ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

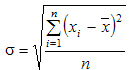
29. Определение функции распределения.

Функцией распределения случайной величины называют вероятность того, что случайная величина примет частное значение меньшее некоторого фиксированного, т.е.

P(X<x) =F(x).

Геометрически это равенство можно истолковать так: функция распределения F(x) есть вероятность того, что случайная величина X примет значение, которое изображается точкой, лежащей левее точки x.

Так как случайная дискретная величина может принимать значения   то функция распределения для нее будет

 .