2к4с Математическая статистика и прогнозирование / МС / Практические работы / матстат / Kontrolnaya_rabota_Matematicheskaya_statistika_i_prognozirovanie

ФГБОУ ВПО «Саратовский государственный технический университет»

Имени Гагарина Ю.А.

Балаковский институт техники, технологии и управления

Кафедра «ИНФОРМАЦИОННЫЕ СИСТЕМЫ И ТЕХНОЛОГИИ»

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Математическая статистика и прогнозирование.

Прогнозирование временных рядов»

Вариант №0

Выполнила:

студент группы

№ зачетной книжки:

Преподаватель:

Штырова И. А.

Балаково 20

Задача 1. Размер обработанных на некотором станке деталей может быть рассмотрен как случайная величина Х, распределенная по нормальному закону. Для контроля качества деталей было произведено 50 измерений. Результаты измерений приведены в табл. 1

1. Провести группировку данных, разбив варианты на 8 интервалов.

2. Для сгруппированного ряда построить гистограмму частот.

3. Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.

4. Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95.

5. Проектный размер детали должен быть равен а (табл. 6.2). При уровне значимости α=0,05 проверить утверждение производителя о совпадении размера произведенных деталей с проектным размером.

Таблица 1

N1	0	N1	0	N1	0	N1	0	N1	0
i	xi	i	xi	i	xi	i	xi	i	xi
1	6,42+N2= 11,42	11	6,42+N2= 11,42	21	7,69+N2= 12,69	31	3,77+N2= 8,77	41	4,91+N2= 9,91
2	2,74+N2= 7,74	12	11,45+N2= 16,45	22	7,74+N2= 12,74	32	9,63+N2= 14,63	42	11,71+N2= 16,71
3	9,28+N2= 14,28	13	6,55+N2= 11,55	23	5,24+N2= 10,24	33	9,96+N2= 14,96	43	11,83+N2= 16,83
4	6,66+N2= 11,66	14	8,52+N2= 13,52	24	7,84+N2= 12,84	34	13,55+N2= 18,55	44	11,89+N2= 16,89
5	4,66+N2= 9,66	15	6,64+N2= 11,64	25	6,91+N2= 11,91	35	10,51+N2= 15,51	45	12,91+N2= 17,91
6	1,41+N2= 6,41	16	4,24+N2= 9,24	26	7,97+N2= 12,97	36	10,80+N2= 15,80	46	4,99+N2= 9,99
7	10,86+N2= 15,86	17	6,86+N2= 11,86	27	8,44+N2= 13,44	37	13,46+N2= 18,46	47	13,54+N2= 18,54
8	7,79+N2= 12,79	18	7,95+N2= 12,95	28	6,64+N2= 11,64	38	11,02+N2= 16,02	48	10,37+N2= 15,37
9	5,47+N2= 10,47	19	6,98+N2= 11,98	29	8,58+N2= 13,58	39	16,92+N2= 21,92	49	15,92+N2= 20,92
10	6,33+N2= 11,33	20	7,48+N2= 12,48	30	9,09+N2= 14,09	40	11,34+N2= 16,34	50	11,21+N2= 16,21

Таблица 2

N	0
a	10+N2	15

Решение.

1. Проведем группировку исходных данных. Найдем разность между наибольшим и наименьшим значениями признака x_max – x_min = 21,92 – 6,41 = 15,51. Тогда длина интервала составит h = 15,51/8 = 1,94 ≈ 1,1. Выберем границы интервалов (табл. 3).

Таблица 3

i	Интервал	Середина интервала xi	Частота ni	Относительная частота wi= ni/n
1	6,41-8,35	7,4	2	0,1
2	8,35-10,29	9,3	6	0,12
3	10,29-12,23	11,3	11	0,18
4	12,23-14,17	13,2	11	0, 26
5	14,17-16,11	15,1	8	0,14
6	16,11-18,05	17,1	7	0,14
7	18,05-19,99	19,1	3	0,04
8	19,99-21,92	20,9	2	0,02
Σ			50	1

2. Построим для сгруппированного ряда гистограмму частот.

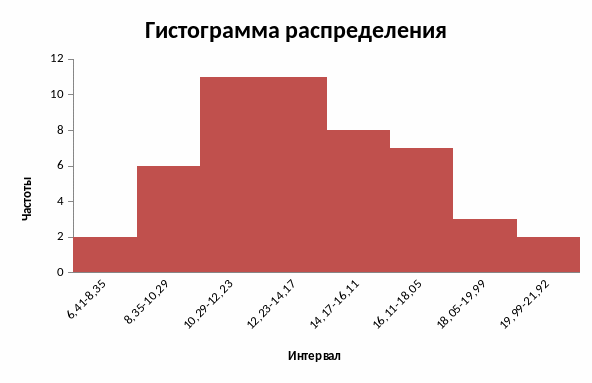
3. Найдем выборочную среднюю

.

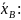
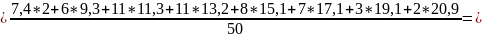
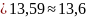Найдем выборочную дисперсию D_в :

.

Найдем исправленную выборочную дисперсию:

.

Найдем исправленное выборочное среднеквадратическое отклонение случайной величины Х:

.

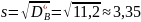4. Построим доверительный интервал для генеральной средней с уровнем доверительной вероятности γ = 0,95. Найдем значение t_1–γ,n–1 = t_0,05;49 по таблице критических точек распределения Стьюдента (приложение 2) при уровне вероятности α = 0,05 и числе степеней свободы k = n – 1 = 49. Получаем t_0,05;49 = 2,01. Далее находим точность оценки:

.

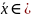
Доверительный интервал для генеральной средней имеет вид . Подставляя значения, получаем, что с вероятностью 0,95 выполнено .

Построим доверительный интервал для генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95. Найдем значение по таблице критических точек распределения χ² (приложение 3) при уровне вероятности (1 + γ)/ 2 = 0,975 и числе степеней свободы:

k =n – 1 = 49.

Получаем = 31,55, следовательно, 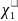=5,62. Найдем значение по таблице критических точек распределения χ² при уровне вероятности (1 – γ)/2 = 0,025 и числе степеней свободы k = n – 1 = 49. Получаем = 70,22, следовательно, = 8,38.

Доверительный интервал для генерального среднеквадратического отклонения имеет вид:

.

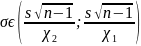Подставляя значения, получаем, что с вероятностью 0,95 выполнено

или

5. При уровне значимости α = 0,05 проверим утверждение, что среднее значение величины Х соответствует проектному значению a = 15. Так как выборка имеет большой объем (n = 50 > 30), то для проверки нулевой гипотезы Н₀: x = а в качестве критерия проверки можно принять случайную величину U. При этом в качестве генерального среднеквадратического отклонения σ можно принять выборочное значение s.

Вычислим наблюдаемое значение критерия:

.

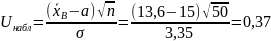Конкурирующей является гипотеза Н₁: x ≠ а, поэтому критическую точку U_кр находим по таблице функции Лапласа (приложение 1) из условия Φ(U_кр) = (1 – α)/2 = 0,475. Получаем U_кр=1,96. Так как |U_набл| < U_кр, то нет оснований отвергнуть нулевую гипотезу. Следовательно, утверждение, что среднее значение выходного параметра Х соответствует проектному значению, является статистически обоснованным.

Задача 2. Была исследована зависимость случайной величины Y от величины Х. В результате 10 испытаний были получены следующие результаты (табл. 4). По этим данным:

1. Построить диаграмму рассеяния.

2. Построить линейное уравнение регрессии.

3. Построить параболическое уравнение регрессии.

4. Для построенных моделей проверить адекватность по F-критерию.

5. По модели с наименьшей остаточной дисперсией вычислить прогнозируемое значение y* при заданном значении x* (табл. 5).

6. Вычислить выборочный линейный коэффициент корреляции.

7. При уровне значимости α=0,05 проверить значимость коэффициента корреляции.

Таблица 4

N1	i	1	2	3	4	5	6	7	8	9	10
0	xi	2,41	5,72	6,46	7,21	7,62	7,93	8,13	8,39	10,45	11,83
	yi	69,07	94,81	97,66	99,93	99,50	99,94	99,75	99,84	93,98	85,01

Таблица 5

N1	0
x*	12

Решение.

Вводим исходные данные, по которым строим точечную диаграмму (рис.1).

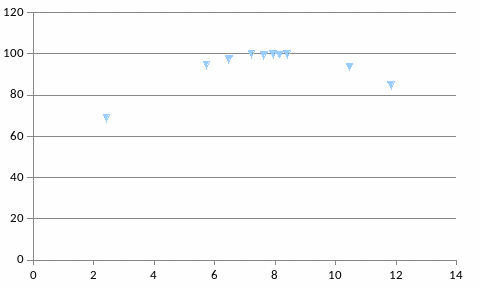
Рис.1. Диаграмма рассеяния

На вкладке РАБОТА С ДИАГРАММАМИ выбираем МАКЕТ – АНАЛИЗ – ЛИНИЯ ТРЕНДА – ДОПОЛНИТЕЛЬНЫЕ ПАРАМЕТРЫ ЛИНИИ ТРЕНДА.

Отмечаем необходимый вид линии (линейная) и опции «Показать уравнение на диаграмме», «Поместить на диаграмму величину достоверности аппроксимации» (рис.2).

Рис.2. Добавление линии тренда

Аналогично добавляем полиномиальную (степень-2) линию тренда. Результат приведен на рис.3.

Рис.3

По значениям R² можно сделать вывод, что полиномиальное уравнение второй степени более точно описывает зависимость величин.

Для обеих моделей проверим адекватность по F-критерию. Имеем линейное уравнение y_i = −81,931+1,578x_i и полиномиальное уравнение второй степени

+15,93 . В табл. 2 внесем данные, необходимые для проверки адекватности моделей (столбцы Yлин и Yпараб, получаем подстановкой значений Х в соответствующие уравнения регрессии).

Таблица 6

Х	У	Улин	(Y-Yлин)^2	(Yлин-Усред)^2	Упараб.	(У-Упараб.)^2	(Yпараб-Yсред)^2
2,41	69,07	85,7340	277,6882	67,4866	69,0455	0,0006	620,1831547
5,72	94,81	90,9572	14,8444	8273,2050	94,8743	0,0041	0,856156699
6,46	97,66	92,1249	30,6376	8486,9935	97,6529	0,0001	13,71882069
7,21	99,93	93,3084	43,8459	8706,4538	99,3520	0,3341	29,19234027
7,62	99,5	93,9554	30,7430	8827,6097	99,8054	0,0933	34,29772268
7,93	99,94	94,4445	30,2001	8919,7711	99,9252	0,0002	35,71441615
8,13	99,75	94,7601	24,8987	8979,4841	99,9004	0,0226	35,41962331
8,39	99,84	95,1704	21,8050	9057,4088	99,7488	0,0083	33,6371794
10,45	93,98	98,4211	19,7234	9686,7129	93,7697	0,0442	0,032155304
11,83	85,01	100,5987	243,0088	10120,1065	85,0190	0,0001	79,74526506
Сумма			737,3950	81125,2320		0,5077	882,7968
Усреднее	93,949

Проверяем адекватность линейного уравнения регрессии на уровне значимости α = 0,05. Вычисляем остаточную дисперсию:

.

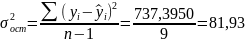Вычисляем дисперсию уравнения регрессии:

Находим наблюдаемое значение критерия:

.

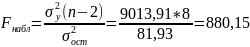Находим критическое значение критерия с помощью функции FРАСПОБР(0,05;1;8). Получим F_крит=5,32. Так как F_набл > F_крит, то уравнение регрессии является значимым, т.е. статистически подтверждается наличие линейной связи между факторным и результативным признаком.

Проверяем адекватность полиномиального уравнения регрессии на уровне значимости α = 0,05. Вычисляем остаточную дисперсию

Вычисляем дисперсию уравнения регрессии:

.

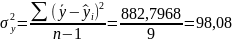Находим наблюдаемое значение критерия:

.

Так как F_набл > F_крит, то уравнение полиномиальной регрессии является значимым.

Таким образом, как линейное, так и экспоненциальное уравнения регрессии адекватно описывают экспериментальные данные. Однако остаточная сумма квадратов линейного уравнения регрессии S_лин =737,3950 существенно больше остаточной суммы квадратов полиномиального уравнения регрессии S_параб =0,5077. Следовательно, полиномиальное уравнение регрессии является более предпочтительным.

По модели с наименьшей остаточной дисперсией вычисляем прогнозируемое значение y* при заданном значении x*=12:

=203,63

Вычислим выборочный линейный коэффициент корреляции. Для этого воспользуемся функцией КОРРЕЛ, где массив1 и массив2 - заданные значения Х и У.

Получили r =0,40749. Между переменными существует обратная линейная зависимость.

Проверим значимость коэффициента корреляции, т.е. проверяем статистическую обоснованность нулевой гипотезы о равенстве нулю генерального коэффициента корреляции H₀: ρ = 0 при альтернативной гипотезе H₁: ρ ≠ 0. Вычисляем наблюдаемое значение критерия Стьюдента :

С помощью функции СТЬЮДРАСПОБР(0,05;8) находим критическое значение T_крит=1,960133. Так как T_набл<T_крит, то гипотеза H₀ принимается, т.е. коэффициент корреляции признается существенно не отличающимся от нуля.

Задача 3. На основе приведенных в таблице 7 данных о производстве продукции (в млн. руб.):

1. Проведите сглаживание уровней ряда с помощью трехчленной скользящей средней.

2. Проведите аналитическое выравнивание и выразите общую тенденцию роста каждого вида продукции соответствующими математическими уровнями, определите выровненные уровни ряда динамики и нанесите их на график с фактическими данными.

3. По построенному тренду сделайте прогноз по выпуску продукции на 2013 год.

Таблица 7

N1	годы
	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012
0	1036,3	1062,2	1072,4	1127,6	1151,1	1148,3	1152,5	1134,5	1191,7	1233,0

Решение.

1. Проведем сглаживание уровней ряда динамики с помощью трехчленной скользящей средней:

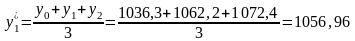
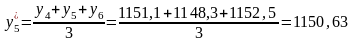
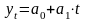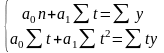2. Проведем аналитическое выравнивание. Найдем уравнение линейной зависимости: . Коэффициенты прямой определяются методом наименьших квадратов из решения системы нормальных уравнений: , где t обозначает время.