2к4с Математическая статистика и прогнозирование / МУ к самостоятельной работе

В рассмотренном примере имеется только один такой сдвиг, которому соответствует ранг, равный 5. Поэтому эмпирическое значение критерия бу-

дет численно равно этому рангу: 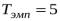. Критическое значение на уровне значимости 5%.

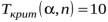Так как 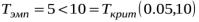, то нулевую гипотезу следует отвергнуть и считать различия существенными.

Тема 3. Регрессионный и корреляционный анализ

Построение доверительного интервала для коэффициента корреляции

Для оценки надежности полученного коэффициента корреляции определяют его погрешность по формуле:

В предположении, что (Х,Y) имеет нормальное распределение или близкое к нему, можно считать коэффициент корреляции распределенным нормально с параметрами r и r.

Корреляционное отношение

Универсальным показателем тесноты связи является теоретическое корреляционное отношение:

ного признака, отражает влияние на вариацию у всех остальных факторов кроме х.

По правилу сложения дисперсий:

21

Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока)

Корреляционное отношение обладает следующими свойствами:

1. Корреляционное отношение всегда находится между нулем и единицей

корреляционная зависимость между признаками Y и X; чем ближе y к ну-

x

лю, тем эта зависимость слабее.

5. Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции:

6. Если y равно абсолютной величине выборочного коэффициента

x

корреляции, то имеет место точная линейная корреляционная зависимость.

Множественная регрессия

Множественный коэффициент корреляции в случае зависимости ре-

зультативного признака от двух факторов вычисляется по формуле:

где ryx1 , ryx2 , rx1x2 – парные коэффициенты корреляции между признака-

ми.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: 0 R 1.

22

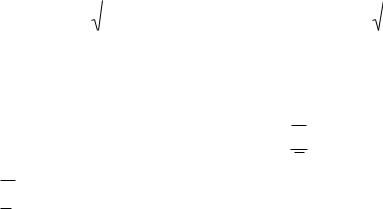
Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:

где R2 – коэффициент множественной детерминации (R2 R2 y / x1x2 );

k – число факторных признаков, включенных в уравнение регрессии.

свободы ν1 = k, ν2 = n – k – 1.

Частные коэффициенты корреляции характеризуют степень тесноты связи результативного признака и фактора, при элиминировании его взаимосвязи с остальными факторами, включенными в анализ. Расчет частных коэффициентов корреляции в случае двухфакторной регрессии (в первом случае исключено влияние факторного признака х2, во втором – х1):

где r – парные коэффициенты корреляции между указанными в индексе переменными.

Для оценки сравнительной силы влияния факторов, по каждому фак-

тору рассчитывают частные коэффициенты эластичности:

Эxi ai xyi ,

где xi – среднее значение соответствующего факторного признака;

y – среднее значение результативного признака;

ai – коэффициент регрессии при i-м факторном признаке.

Данный коэффициент показывает, на сколько процентов следует ожидать изменения результативного показателя при изменении фактора на 1% и неизменном значении других факторов.

Частный коэффициент детерминации показывает, на сколько про-

центов вариация результативного признака объясняется вариацией i-го признака, входящего в множественное уравнение регрессии, рассчитывается по формуле:

d xi ryxi xi ,

где ryxi – парный коэффициент корреляции между результативным и i-м

факторным признаком;

xi – соответствующий стандартизованный коэффициент уравнения множественной регрессии:

23

Пример. Имеются некоторые данные о среднегодовой стоимости ОПФ (СОПФ), уровне затрат на реализацию продукции (ЗРП) и стоимости реализованной продукции (РП). Считая зависимость между этими показателями линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели.

Решение. Составим систему нормальных уравнений МНК:

10a0 66a1 90a2 294;66a0 490a1 688a2 2078;90a0 688a1 1018a2 2880;

Выразим из 1-го уравнения системы a0 = 29,4 – 6,6·a1 – 9·a2. Подставив во 2-е уравнение это выражение, получим:

Далее подставляем в 3-е уравнение вместо a0 и a1 полученные выражения и решаем его относительно a2 с точностью не менее 3-х знаков после запятой. Итак:

tрасчx1 =5,00 > tтабл=3,50 – коэффициент корреляции x1 значим; tрасчx2 =3,27 < tтабл=3,50 – коэффициент корреляции x2 не значим.

Произведенные расчеты подтверждают условие включения факторных признаков в регрессионную модель – между результативным и факторными признаками существует тесная связь ( rx1 y = 0,884; rx2 y = 0,777),

однако между факторными признаками достаточно существенная связь ( rx1x2 = 0,893). Включение в модель фактора x2 незначительно увеличивает

коэффициент корреляции ( rx1 y = 0,884; R y / x1x2 =0,893), поэтому включение

в модель фактора x2 нецелесообразно.

Вычислим стандартизованные коэффициенты уравнения множественной регрессии:

т.е. вариация результативного признака объясняется главным образом вариацией фактора x1.

Вычислим частные коэффициенты эластичности:

Проверим адекватность модели на основе критерия Фишера:

Найдем значение табличного значения F-критерия для уровня значимости α=0,05 и числе степеней свободы ν1 = 2, ν2 = 10 –2 – 1 : Fтабл=4,74. Превышение значения Fрасч над значением Fтабл позволяет

25

считать коэффициент множественной детерминации значимым, а соответственно и модель – адекватной, а выбор формы связи - правильным.

Тема 4. Моделирование временных рядов и прогнозирование

Стохастические временные ряды

Стохастическим (случайным) процессом называется процесс, который развивается во времени в соответствии с законами теории вероятностей.

Случайным процессом X(t) на множестве Т называют функцию, значения которой случайны при каждом t T. Если элементы Т счетные (дискретное время), то случайный процесс часто называют случайной последовательностью.

Полное математическое описание случайного процесса предполагает задание системы функций распределения:

–для каждого t T Ft ( x) P( X (t) x) ,

–для каждой пары элементов t1 , t2 T

Ft1 ,t2 (x1 , x2 ) P( X (t1 ) x1 , X (t2 ) x2 )

и вообще для любого конечного числа элементов

t1 , t2 ,..., tn T

Ft1 ,t2 ,...tn (x1 , x2 ,... xn ) P( X (t1 ) x1 , X (t2 ) x2 ,..., X (tn ) xn ) .

Функции называют конечномерными распределениями случайного процесса. Построить такую систему функции для произвольного случайного процесса практически невозможно. Обычно случайные процессы задают с помощью априорных предположений о его свойствах, таких как независимость приращений, марковский характер траекторий и т. п.

В теории временных рядов используются ряд моделей случайной составляющей, начиная от простейшей – «белого шума», до весьма сложных типа авторегрессии – скользящего среднего и других, которые строятся на базе белого шума.

Белый шум

Прежде чем определять процесс белого шума рассмотрим последовательность независимых случайных величин, для которой функция распределения есть

Ft1 ,t2 ,...tn (x1 , x2 ,... xn ) Ft1 (x1 ) Ft2 (x2 ) ... Ftn (xn ) .

Из последнего соотношения следует, что все конечномерные распределения последовательности определяются с помощью одномерных распределений.

Если к тому же в такой последовательности составляющие ее случайные величины X(t) имеют нулевое математическое ожидание и распределены одинаково при всех t T, то это – «белый шум». В случая нормаль-

26

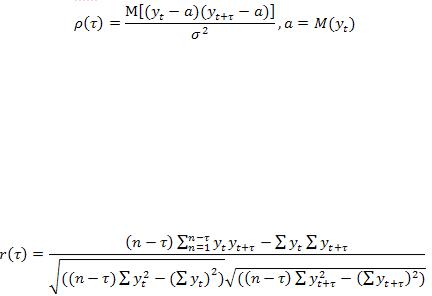
ности распределения X(t) говорят о гауссовском белом шуме. Итак, гауссовский белый шум – последовательность независимых нормально распределенных случайных величин с нулевым математическим ожиданием и одинаковой (общей) дисперсией.

Стационарные временные ряды

Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени.

Рассмотрим два ряда y1, y2,…, yn и y1+τ, y2+τ,…, yn+τ. Эти ряды называются сдвинутыми относительно друг друга на τ единиц или с лагом τ.

Временной ряд yt (t=1, 2,…, n) называется строго стационарным, если совместное распределение вероятностей n наблюдений y1, y2,…, yn такое

же, как и n наблюдений y1+ τ, y2+ τ,…, yn+ τ при любых n, t, τ.

Таким образом, свойство строго стационарных рядов не зависят от момента времени t, т. е. в таких рядах от момента времени t не зависит закон распределения и числовые характеристики временного ряда.

Степень тесноты связи между последовательными наблюдениями

временного ряда y1,y2,…, yn и y1+τ, y2+τ,…, yn+τ может быть оценена с помощью коэффициента корреляции:

Так как коэффициент ρ(r) измеряет корреляцию членами одного и того же временного ряда, то его называют коэффициентом автокорреляции, а зависимость ρ от r — автокорреляционной зависимостью.

В силу стационарности временного ряда yt автокорреляционная функция ρ(t) зависит только от лага τ и является четной функцией. Таким образом, при изучении автокорреляционной функции можно ограничится только положительным сдвигом τ.

Статистической оценкой ρ является выборочный коэффициент автокорреляции, определяемый по формуле:

Функцию r(τ) называют выборочной автокорреляционной функцией, а её график — коррелограммой.

При расчете r(τ) следует помнить, что с увеличением τ число n-τ пар наблюдений в значении случайной величины уменьшается, поэтому лаг τ должен быть таким, чтобы n-τ было достаточно для вычисления r(τ).

Обычно ориентируются на соотношении τ. Для стационарного временного ряда с увеличением лага τ взаимосвязь между членами временных рядов yt и yt+τослабевает, и автокорреляционная функция должна убывать по абсолютной величине.

27

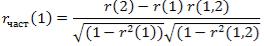
Наряду с автокорреляционной функцией при исследовании стационарных временных рядов рассматривается частная автокорреляционная функция ρчаст(r), где ρчаст — это частный коэффициент корреляции между рядами yt и yt+τ, то есть коэффициент корреляции между yt и yt+τ при устранении влияния промежуточных членов временных рядов.

Статистической оценкой ρчаст является выборочная авокорреляционная функция rчаст (τ), где rчаст — выборочный частный коэффициент корреляции. Выборочный частный коэффициент автокорреляции первого порядка между членами ряда yt и yt+2 (при устранении влияния промежуточного ряда yt+1) может быть вычислен по формуле:

Модели авторегрессии

Процессом авторегрессии порядка p называется случайный ряд вида: x(k) - μ = a1*[x(k-1) - μ] + a2*[x(k-2) - μ] + ...+ ap*[x(k-p) - μ] + ε(k)

где: x(k) - k-ое значение временного ряда;

a1, a2, ..., ap - коэффициенты процесса авторегрессии; μ - математическое ожидание временного ряда;

ε(k) - k-ое значение непрогнозируемого временного ряда ("белый

шум").

Как видно значение временного ряда определяется p предыдущими значениями ряда плюс значение случайной составляющей. Для более компактной записи моделей временных рядов используют оператор сдвига Z:

x(k-1) = Z*x(k); x(k-2) = Z2*x(k); ... x(k-p) = Zp*x(k)

С использованием оператора сдвига процесс авторегрессии порядка p может быть представлен следующим образом:

(1 -a1*Z - a2*Z2 - ... -ap*Zp)*[x(k) - μ] = ε(k)

выражение (1 -a1*Z - a2*Z2 - ... -ap*Zp) называют оператором авторегрессии порядка p и обозначают: АР(p) - в русской транскрипции или AR(p) - в английской транскрипции. Таким образом, для процесса авторегрессии порядка p имеем:

AR(p)*[x(k) - μ] = ε(k)

Адаптивная модель прогнозирования Брауна

Адаптивные модели прогнозирования — это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий. Инструментом прогноза в адаптивных моделях, как и в кривых роста, является математическая модель с единственным фактором «время».

28

Модель Брауна описывает процессы с линейной и параболической тенденцией (трендом), а также случайные процессы без тенденции. Построение линейной модели Брауна имеет следующие этапы:

1. По первым пяти точкам временного ряда с помощью метода наименьших квадратов оцениваются значения параметров линейной модели для нулевого момента времени:

yth(t) = a0 + a1t .

2. С использованием параметров a0 и a1 , найденных на предыдущем этапе, находим прогноз на шаг вперед ( = 1):

y1 = a0(0) + a1(0) = a0(0) + a1(0) .

3.Находим величину отклонения фактического значения экономического показателя от расчетного (в данном случае t = 1):

= y(t) – yth(t) . (1)

4.Корректируем параметры модели по формулам:

a0(t) = a0(t-1) + a1(t-1) + (1 – 2)(t) , (2)

a1(t) = a1(t-1) + (1 – )2(t) , (3)

где = 1 – , – параметр сглаживания.

5. С помощью скорректированных на предыдущем шаге параметров находим прогноз на следующий момент времени ( = 1):

yth() = a0(t) + a1(t) .

Точечный прогноз на будущее рассчитывается по формуле yth(n + ) = a0(n) + a1(n) , = 1, 2, …

Здесь n – число наблюдений.

ВОПРОСЫ И ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ

1.Какая статистическая модель применима для выборки, полученной следующим образом: 10 раз подсчитывалось число гербов при бросании трех монет?

2.Какая статистическая модель применима для выборки действующих цен на 1 литр молока в 50 различных магазинах города?

2.Дайте определение параметрической модели.

3.Дайте определение вариационного ряда.

4.Можно ли восстановить по вариационному ряду выборку?

5.Дайте определение эмпирической функции распределения.

6.Какими свойствами обладает эмпирическая функция распределе-

ния?

7.Можно ли восстановить по эмпирической функции распределения вариационный ряд?

8.Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратичное отклонение этой величины соответственно равны 6 и 2. Найти вероятность того, что в результате испытания

Хпримет значение, заключенное в интервале [4, 8].

29

9. Вычислить вероятность того, что отклонение нормально распределенной случайной величины Х по абсолютной величине меньше заданного положительного числа для вариантов: = σ, = 2σ, = 3σ.

10.Производится измерение диаметра вала (без систематических ошибок). Случайные ошибки измерения Х подчинены нормальному закону со средним квадратичным отклонением 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

11.Прогноз экспертов относительно величины банковской процентной ставки в будущем году подчиняется нормальному распределению с

параметрами 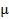= 10% годовых и 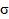= 2% годовых. Определить вероятность того, что в будущем году банковская процентная ставка превысит 15% годовых.

12.Случайная величина распределена по закону Пирсона (хи-квадрат)

счислом степеней свободы равным 16. Найти значение квантиля уровня

0,99.

13.Случайная величина распределена по закону Пирсона (хи-квадрат)

счислом степеней свободы 10. Найти интервал, в который случайная величина попадает с вероятностью 0,9.

14.Найти симметричный интервал, в который случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы, попадает

свероятностью 0,9.

15.Найти значение x из условия P(t > x)=0,995, где t – случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы.

16.Случайная величина Х распределена по закону Фишера с числом степеней свободы m = 7 и n =12. Найти значение квантиля уровня 0,99.

17.Найти значение x из условия P(F< x)=0,95, где F – случайная величина, распределенная по закону Фишера со степенями свободы m = 23 и n =35.

18.Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:

30