2к4с Математическая статистика и прогнозирование / МУ к самостоятельной работе

ВВЕДЕНИЕ

Цель работы - формирование у студентов, изучающих дисциплину «Математическая статистика и прогнозирование», умений и навыков самостоятельной учебной деятельности как при выполнении самостоятельных работ на аудиторных занятиях, так при выполнении внеаудиторной самостоятельной работы.

Виды самостоятельной работы, реализуемые в дисциплине «Математическая статистика и прогнозирование»:

1. Самостоятельное изучение теоретического курса, включающее:

а) самостоятельное изучение теоретического материала с использованием рекомендуемой литературы;

б) подготовка устных ответов на контрольные вопросы, приведенные после каждой темы.

2. Самостоятельное освоение практического курса, включающее самостоятельную работу по решению задач.

По каждому виду работы студент должен выполнить задания, приведенные в данных методических указаниях по самостоятельной работе.

.

ТЕМЫ, ИЗУЧАЕМЫЕ В КУРСЕ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА И ПРОГНОЗИРОВАНИЕ

Математическая статистика – раздел математики, изучающий методы сбора, систематизации и обработки наблюдений с целью выявления статистических закономерностей.

Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений.

Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Например, целью исследования может быть:

-оценка неизвестной вероятности события;

-оценка параметров распределения случайной величины;

-оценка неизвестной функции распределения случайной величины;

-проверка гипотез о параметрах распределения или о виде неизвестного распределения;

-оценка зависимости случайной величины от одной или нескольких случайных величин и т.д.

Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала.

2

Тема 1. Основы выборочного метода и элементы статистический теории оценивания

Свойства распределений Пирсона, Стьюдента и Фишера

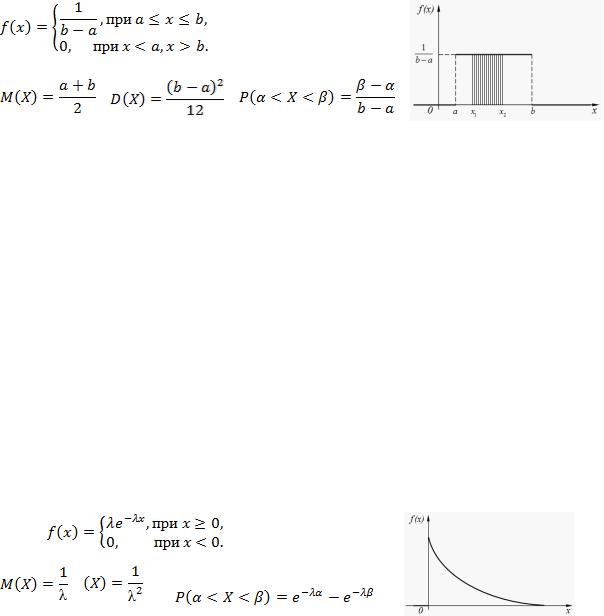
Равномерный закон распределения. Непрерывная случайная величи-

на X имеет равномерный закон распределения на отрезке [a, b], если ее

плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.

Примеры случайных величин, имеющих равномерное распределение

– время ожидания автобуса, ошибка при взвешивании, измерении. Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задача массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению.

Пример 1. Измерения проводят линейкой с ценой деления 1 мм. Показания измерений округляют до ближайшего целого значения. а) Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,1 мм. б) Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х, равномерно распределенной в интервале [0; 1].

а) Р(0,1<Х<0,9) = (0,9 - 0,1) / (1 - 0) = 0,8, т.е. 80%.

б) МХ = (0 + 1)/ 2 = 0,5; DX = (1 - 0)2 /12 = 0,08 и σ(Х) = 0,29.

Показательный (экспоненциальный) закон распределения. Непре-

рывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром λ >0, если ее плотность вероятности имеет вид:

Примеры случайных величин, имеющих показательное распределение – период времени работы прибора между поломками, затраты времени на обслуживание одного станка. Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.

Пример 2. Длительность времени безотказной работы элемента имеет показательное распределение с параметром = 0,01. Найти вероятность

3

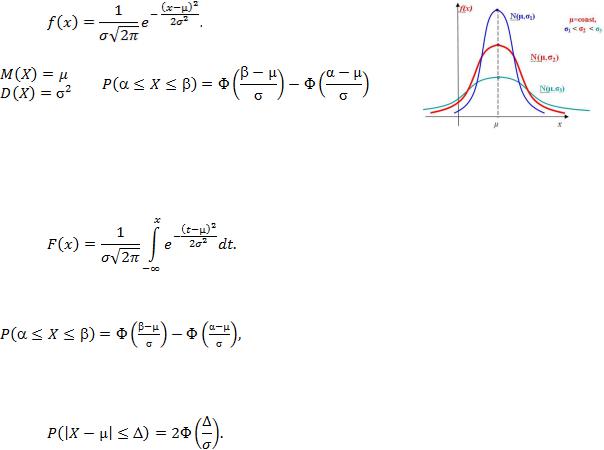
того, что за время длительностью 50 часов: а) элемент откажет; б) элемент не откажет.

а) Р(0 <X<50) = 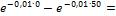1 – 0,607 = 0,393, т.е. с вероятностью

39,3% элемент откажет за период времени 50 часов.

б) 1 – 0,393 = 0,607, т.е. с вероятностью 60,7% элемент не откажет.

Нормальный закон распределения. Непрерывная случайная величина X

имеет нормальный закон распределения с параметрами a и 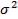, если ее

плотность вероятности имеет вид:

Обозначение:

Нормальный закон распределения с параметрами 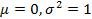, т.е.

N(0;1), называется стандартным или нормированным.

Функция распределения нормально распределенной случайной величины имеет вид:

Вероятность попадания случайной величины X, распределенной по нормальному закону, в интервал [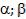], равна:

где 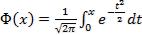– функция Лапласа.

Функция Лапласа нечетная: Ф(-x) = - Ф(х), ее значения затабулированы. Вероятность попадания случайной величины в интервал, симметрич-

ный относительно математического ожидания :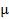

Если 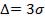, то 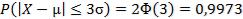. Отсюда следует правило "трех сигм": если 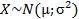, то практически достоверно, что значения случайной величины Х заключены в интервале .

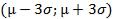Нормальное распределение возникает всегда, когда на величину влияет большое количество случайных факторов (и ни один из них не является доминирующим). Нормальный закон распределения занимает центральное место в теории и практике вероятностно-статистических методов. Он является предельным законом, к которому приближаются многие другие законы распределения.

Пример 3. Случайная величина Х распределена нормально с параметрам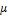и =8 и =3. Найти вероятность того, что случайная величина попадет в интервал [12,5; 14].

Р(12,5<Х<14) = 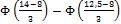= Ф(2) – Ф(1,5) = 0,4772 – 0,4332 =

0,0440, т.е. с вероятностью 4,4% случайная величина попадет в заданный

4

интервал.

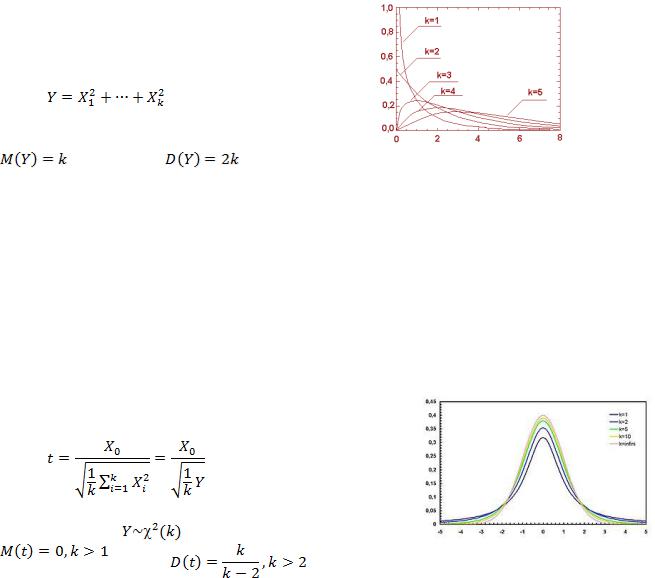
Распределение хи-квадрат 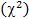. Распределением Пирсона или хиквадрат 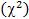с k степенями свободы называется распределение суммы квадратов k независимых случайных величин, распределенных по стандартному нормальному закону.

Пусть 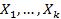– совместно независимые стандартные нормальные случайные величины, т.е. 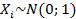, тогда случайная величина

имеет распределение хи-квадрат с k степенями свободы.

Обозначение: 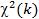Распределение 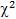затабулировано. Распределение 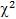зависит от одно-

го параметра k – числа степеней свободы. С возрастанием k распределение 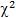приближается к нормальному закону распределения (при k ≥ 30 распределение 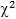практически не отличается от нормального. В математической статистике распределение хи-квадрат используется для построения интервальных оценок и статистических критериев.

Распределение Стьюдента (t-распределение).

Пусть 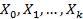– независимые стандартные нормальные случайные величины, такие, что 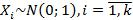. Тогда распределение случайной величины t:

называется распределением Стьюдента с k степенями свободы, .

Обозначение: .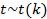

Распределение Стьюдента затабулировано. Распределение Стьюдента сходится к стандартному нормальному при 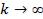. Распределение Стьюдента применяется в статистике для построения доверительных интервалов

итестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения.

Распределение Фишера (Фишера-Снедекора).

Пусть 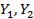– независимые случайные величины, имеющие распределение хи-квадрат со степенями свободы m

иn соответственно: 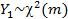, 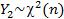. Тогда распреде-

ление случайной величины

5

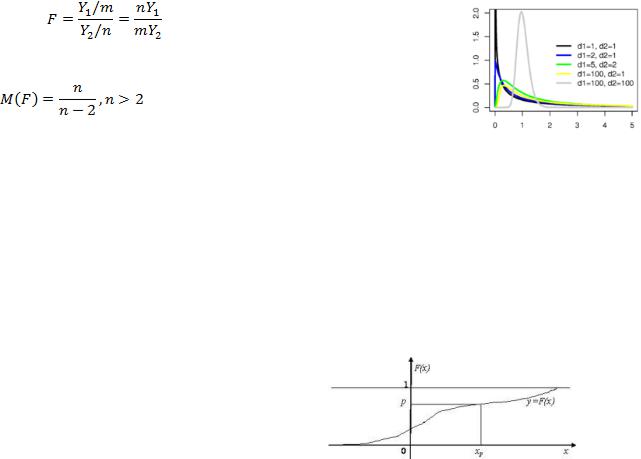
называется распределением Фишера со степенями свободы m и n.

Обозначение: 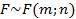Распределение Фишера затабулировано. Распределение Фишера ис-

пользуют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и др.

Квантили распределений

При статистической обработке данных, нахождении доверительных границ для параметров распределений случайных величин и во многих иных случаях используется такое понятие, как квантиль порядка р, где 0 < p < 1. Квантиль – это функция обратная F(x), аргумент функции – вероятность р.

Квантилью распределения случайной величины Х, отвечающей вероятности р, называется такое значение хр, которое случайная величина Х не превосходит с вероятностью р:

Р(Х< xp) = p = F(xp ).

На практике распределения Пирсона, Стьюдента и Фишера используют, как правило, не в виде зависимостей, а находя квантили, соответствующие заданной вероятности.

Пример 4. Случайная величина распределена по закону Пирсона (хиквадрат) с числом степеней свободы равным 20. Найти интервал, в который случайная величина попадает с вероятностью 0,95.

Примем, что заштрихованные области равны между собой (см. рис. 4), т.е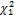. P(<) =0,95 и P(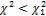) = P(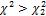) = (1-0,95) /2 = 0,025.

Для правой границы P(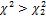) = 0,025. По Приложению 5 находим

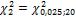=34,2.

Для левой границы P(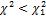) = 1 - P(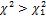), т.е. левую границу ищем как правую для P(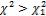) = 1 - P(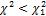) = 1 – 0,025 = 0,975. По Приложению 5 находим 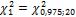=9,59.

Следовательно, значение случайной величины, распределенной по закону 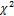с числом степеней свободы k = 20, с вероятностью 0,95 принадлежит интервалу [9,59; 34,2].

Пример 5. Случайная величина Х распределена по закону Стьюдента с числом степеней свободы равным 30. Найти симметричный интервал, в который случайная величина попадает с вероятностью 0,98.

6

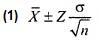
Р(- х < t < х) = Р(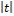< x) = 0,98 и P(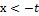) = P(x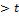) = (1-0,98) /2 = 0,01

По таблице распределения Стьюдента для двусторонней области находим x = 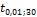= 2,75. Следовательно, значение случайной величины, распределенной по закону Стьюдента с числом степеней свободы k = 30, с вероятностью 0,98 принадлежит интервалу [-2,75; 2,75] .

Пример 6. Случайная величина Х распределена по закону Фишера с числом степеней свободы m = 10 и n =12. Найти значение квантиля уровня

0,99 (см. рис. 6).

Р(F > x) = 1 – 0,99 = 0,01. По Приложению 7 находим х = 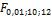= 4,30. Следовательно, квантиль уровня 0,99 случайной величины, распределенной по закону Фишера с числом степеней свободы m = 10 и n =12, равен значению 4,30.

Определение объема выборки

Определение объема выборки для оценки математического ожида-

ния. Чтобы определить объем выборки, необходимый для оценки математического ожидания генеральной совокупности, следует учесть величину ошибки выборочного исследования и доверительный уровень. Кроме того, необходима дополнительная информация о величине стандартного отклонения. Для того чтобы вывести формулу, позволяющую вычислить объем выборки, начнем с формулы (1)

где Х̅– среднее значение выборки, Z — значение стандартизованной нормально распределенной случайной величины, соответствующее интегральной вероятности, равной 1 – α/2, σ — стандартное отклонение генеральной совокупности, n – объем выборки

В этой формуле величина, добавляемая и вычитаемая из X̅, равна половине длины интервала. Она определяет меру неточности оценки, возникающей вследствие ошибки выборочного исследования, которая обозначается символом е и вычисляется по формуле

(2) e = Z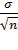

Решив уравнение (2) относительно n, получим:

(3) n =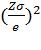

Пример 7. Предположим, что из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Компания желает построить интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%. Как был определен объем выборки? Следует ли его уточнить?

Допустим, что после консультаций с экспертами, работающими в

7

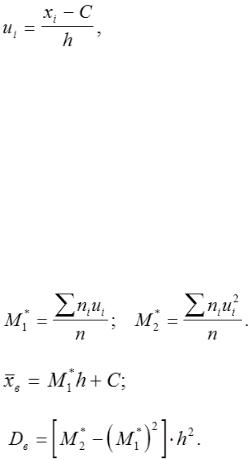
компании, статистики установили допустимую ошибку выборочного исследования равной ±5 долл., а доверительный уровень — 95%. Результаты предшествующих исследований свидетельствуют, что стандартное отклонение генеральной совокупности приближенно равно 25 долл. Таким образом, е = 5, σ = 25 и Z = 1,96 (что соответствует 95%-ному доверительному уровню). По формуле (3) получаем:

Следовательно, n = 96. Таким образом, объем выборки, равный 100, был выбран удачно и вполне соответствует требованиям, выдвинутым компанией.

Метод произведений для вычисления выборочных средней и дисперсии

Метод произведений – это удобная техника вычислений условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная условные моменты, нетрудно найти начальные и центральные эмпирические моменты.

Равностоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условными называют варианты, определяемые равенством:

где С - ложный нуль (новое начало отсчета);

h - шаг, т. е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).

Замечание 1. В качестве ложного нуля можно принять любую варианту Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту)

Замечание 2. Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.

Условные моменты вычисляются по формулам:

Тогда выборочная средняя равна:

и выборочная дисперсия равна:

8

Правило сложения дисперсий

Если исходная совокупность является такой, что по значениям признака она делится на l групп, то общая дисперсия складывается из частных дисперсий.

Сначала вычисляем l частных средних ( x j ), т.е. среднее значение признака в каждой группе:

Общая дисперсия отражает вариацию признака за счет всех факторов, действующих в данной совокупности.

Вариацию между группами за счет признака-фактора, положенного в основу группировки, отражает межгрупповая дисперсия, которая исчисляется как средний квадрат отклонений групповой средней от общей средней:

Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, т.е. вариацию между группами за счет призна- ка-фактора, положенного в основу группировки.

Вариацию внутри каждой группы изучаемой совокупности отражает внутригрупповая дисперсия, которая исчисляется как средний квадрат от-

клонений значений признака х от частной средней x j :

Для всей совокупности внутригрупповую вариацию будет выражать

средняя из внутригрупповых дисперсий, которая рассчитывается как средняя арифметическая из внутригрупповых дисперсий:

9

l

2j n j

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки.

Между представленными видами дисперсий существует определенное соотношение, которое известно как правило сложения дисперсий:

общ2 2 2 .

Таким образом, общая дисперсия складывается из двух слагаемых: первое – средняя из внутригрупповых дисперсий – измеряет вариацию внутри частей совокупности, второе – межгрупповая дисперсия – вариацию между средними этих частей.

Пример 8. Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным о производительности труда в двух бригадах:

Промежуточные расчеты занесем в таблицы: