2к4с Исследование операций / МУ к практической работе 3
.pdfАпробация
РЕШЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Методические указания к выполнению практической работы для студентов направления
230400 очной, заочной и заочно-сокращенной форм обучения
Цель работы: формирование навыков решения задач нелинейного программирования.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Рассмотрим задачу нелинейного программирования, содержащую только две переменные, записанную в виде
,…………….
(x) <
, x = (
) 
.
Функция f (x) называется целевой функцией, а неравенства
, i= 1,.,m называются ограничениями задачи. Множество точек, удовлетворяющих ограничениям задачи, называется допустимым множеством задачи.
Метод множителей Лагранжа
Пусть требуется решить задачу нелинейного программирования следующего вида:
F (
,
,
где функции f и 
, i=
непрерывны, и непрерыв-
ны их частные производные по 
, l=
.
Для решения поставленной задачи может быть применен ме-
2
тод множителей Лагранжа. Объясним идею метода на примере задачи нелинейного программирования, зависящей от двух переменных и имеющие только одно ограничение:
g |
=b. |
Будем исходить из геометрической интерпретации задачи. А именно, заметим, что линия уровня с максимальным значением параметра С будет касаться линии границы в точке, являющейся оптимальным решением задачи (рис.3.3).
Рисунок 3.3 - Геометрическая интерпретация задачи
Поскольку две гладкие линии (имеющие непрерывные част-
ные производные) касаются друг друга в точке 
, то их векто- ры-нормали сонаправлены. Поскольку вектор-нормаль есть градиенты функций (вектор частных производных), то справедливо
векторное соотношение f’ (
) =λg’ (
), где λ есть некоторый коэффициент пропорциональности. Координаторами векто-
ров f’ (
) и g’ (
), являются значения частных производ-
3
ных функций f и g соответственно в точке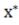
.
’ |
( |
) |
= |
’ |
( |
) |
=
Из условия пропорциональности в точке 
имеем
;
.
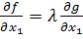Для определения значений 
и 
в которых функция f достигает максимума, к этим уравнениям надо добавить условие
принадлежности точки 
графику функции g (
,
) =b.
Окончательно получаем систему уравнений, определяющую оптимальное решение поставленной задачи
Введем новую функцию
4
Тогда последняя система перепишется в виде
Функцию F называют функцией Лагранжа.
Приведем ниже алгоритм метода множителей Лагранжа решения задач нелинейного программирования.
Этап 1. Составляют функцию Лагранжа
( |
) |
=f |
( |
|
|
|
. |
|
Этап 2. Находят частные производные функции Лагранжа по 
и 
i=1,n; j=1,m и приравнивают их к нулю
5
.
Этап З. Решают систему и определяют точки, в которых
функция 
может иметь экстремум. Этап 4. Проверяют полученные на этапе 3 точки на экстре-
мум и определяют экстремальное значение функции f найденной точки.
Рассмотрим применение изученных методов на примере решения задачи оптимальной реализации продукции, в частности для расчета экономико-математической модели при нелинейных затратах на производство. Фирма реализует автомобили двумя способами: через магазин и через торговых агентов. При реали-
зации 
автомобилей через магазин расходы на реализацию составляют 4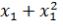
усл. ед., а при продаже 
ав-
томобилей через торговых агентов расходы составляют 
усл. ед. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет 200 шт. Составим математическую модель задачи. Целью является миними-
зация суммарных расходов R =4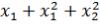
. Управляющие переменные - это число автомобилей, реализуе-
мых первым и вторым способом: 
и 
соответственно (200 шт.). Окончательно математическая модель имеет следующий вид:
=4
,
6
Для ее расчета применим метод множителей Лагранжа. Функция Лагранжа имеет вид
(
4
+λ (200-
.
Найдем частные производные функции F по 
, 
и λ и приравняем их к нулю.
Получим следующую систему уравнений:
Решая систему, найдем 
99, 
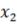= 101, 
=
202, f (
) = 20 398.
Таким образом, для получения минимальных расходов, нужно реализовать 99 автомобилей через магазин и 101 автомобиль через торговых агентов. При этом расходы на реализацию составят 20 398 усл. ед.
Методы штрафных функций
7
Основная идея методов штрафных функций состоит в преобразовании задачи нелинейного программирования при наличии ограничений либо в одну (эквивалентную исходной) задачу без ограничений, либо в эквивалентную последовательность задач без ограничений.
Рассмотрим задачу:
f (x)→min, xRn, (2.1) gi(x) ≥ 0, i = 1, m (2.2) hl (x)=0, l = 1, p.
Предполагается, что точка x* является решением этой задачи, известно некоторое начальное приближение x0, возможно недопустимое, т.е. не удовлетворяющее отношениям (2.2). С помощью рассматриваемых далее алгоритмов в пространстве Rn строится конечная последовательность точек xt, t = 0,1,…, k, которая начинается с заданной точки x0 и заканчивается точкой xk, дающей наилучшее приближение к точке экстремума x* среди всех точек построенной последовательности. В качестве точек последовательности {xt} берутся стационарные точки штрафной функции – целевой функции вспомогательной задачи безусловной минимизации.
Конкретные методы, основанные на указанной общей схеме, определяются видом штрафной функции, а также правилами, по которым производится пересчет штрафных параметров по окончании очередного цикла безусловной минимизации. Идея преобразования задачи с ограничениями в надлежащим образом построенную последовательность задач без ограничений представляется заманчивой, главным образом, в связи с наличием эффективных и надежных методов безусловной минимизации.
8
Рисунок 2.1 – Метод внутренних штрафов
Рисунок 2.2 – Метод внешних штрафов
В зависимости от того, являются ли элементы последовательности {xt} допустимыми или недопустимыми точками, говорят соответственно о методах внутренней (рис. 2.1) или внешней точки (рис. 2.2) Иногда их называют методами внутреннего или
9
внешнего штрафа. Методы внутренних штрафных функций называют также методами барьерных функций.
Понятие штрафных функций Штрафная функция определяется выражением:
P (x, R) = f (x) + H (R, g(x), h(x)), (2.3)
где R – набор штрафных параметров, H – штраф – функции R и ограничений,
H (R, g(x), h (x)) = Rϕ (g(x), h(x)).
Выражение для штрафа H определяется таким образом, чтобы допустимые точки задачи имели преимущество перед недопустимыми в отношении безусловной минимизации штрафной функции.
Методы внутренней точки связаны с такими H, при которых стационарные точки функции P (x, R) оказываются заведомо допустимыми.
Эти методы называют также методами барьеров, поскольку здесь штраф как бы создает вдоль границы допустимой области S барьер из бесконечно больших значений функции P.
Методы штрафных функций представляют большой интерес лишь при выполнении следующих требований:
1) решения подзадач должны стремиться к решению задачи нелинейного программирования вида:
lim xt → x*, t →k < ∞;
2)сложность минимизации P (x, R) должна быть того же порядка, что и для функции f (x);
3)правило пересчета Rt+1 = F(Rt) должно быть простым.
В данной работе мы рассмотрим метод внешней точки (метод внешнего штрафа).
10