
2к3с Математическое моделирование / методические указания к раброте №1
.pdf
cos(x) expand x
При проведении символьных вычислений можно использовать следующие
символьные операторы:
1)float – указывает на то, что результат должен быть выведен в виде числа с плавающей запятой, после слова float должно быть указано количество знаков после запятой, которые должны быть выведены в результате; при символьных вычислениях с использованием оператора float, в отличие от обычных численных расчетов (=), выражение сначала вычисляется аналитически, поэтому максимальное количество знаков после запятой равно 250 (а при численных расчетах - 15). Например,
2)complex – выводит комплексное число в виде a+bi
3)assume – наложение ограничений на параметры выражения
4)solve – решение уравнения или системы уравнения
5)simplify – упрощение выражения, символьный процессор MathCAD
стремится так преобразовать выражение, чтобы оно приобрело более простую форму. При этом используются различные арифметические формулы, приведение подобных слагаемых, тригонометрические тождества, пересчет обратных функций и др. Например,
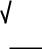
(x 2y) z z2 (x 5y) |
z simplify |
|||
|
x 5 |
y 3 |
|
|
(2x 2y) z z2 (x 5y) |
z simplify |
|||
|
|
|
|
|
|
3 x simplify |
|
||
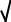 3.01 x simplify
3.01 x simplify
6) substitute – подстановка выражения вместо переменной. Например,
a x2 b x c substitute x |
|
5 |
|
||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
sin |
|
k x |
b x substitute |
k |
|
a x |
b |
|
x |
7)factor. В зависимости от введенного выражения, данный оператор выполняет одно из следующих действий: сворачивает полином в произведение полиномов, раскладывает целое число на простые множители или приводит дроби к общему знаменателю. Например,
x4 16 factor 28 factor
8)expand - операция символьного разложения, или расширения, выражений.
В ходе разложения раскрываются все суммы и произведения, а сложные тригонометрические зависимости разлагаются с помощью тригонометрических тождеств.
9)coeffs – вычисление полиномиальных коэффициентов

(x 2y) |
z z2 y (x 5y) |
z coeffs x |
(x 2y) |
z z2 y (x 5y) |
z coeffs z |
(x 4) |
(x 7) x 99 coeffs x |
|
10) collect – приведение выражения к полиному по заданной переменной
(приведение подобных слагаемых):
(x 2y) z z2 y (x 5y) |
z collec t x |
|
(x 2y) z z2 y (x 5y) |
z collec t y |
|
(x 2y) z z2 y (x 5y) |
z collec t y x |
|
(x 2y) z z2 y (x 5y) |
z collec t x y |
|
11) series – разложение функции в степенной ряд Тейлора. При использовании функции необходимо указать имя переменной, по которой проводится разложение и порядок аппроксимации (количество степенных слагаемых)
sin(x) series x 10
12) parfrac – разложение дроби на простейшие:
11x2 9x 1 convert parfrac x x2 3x 2
13)fourier, invfourier – прямое и обратное преобразование Фурье
14)laplace, invlaplace – прямое и обратное преобразование Лапласа
15)ztrans, invztrans – прямое и обратное Z-преобразование.
Решение уравнений и систем
Для решения уравнений используется функция ROOT
Формат функции: root(выражение,имя_переменной)
Перед использованием функции необходимо
1.построить график левой части уравнения – функции,
2.по графику найти приближенные значения переменной x, которые MathCad
использует как начальное приближение при поиске корня.
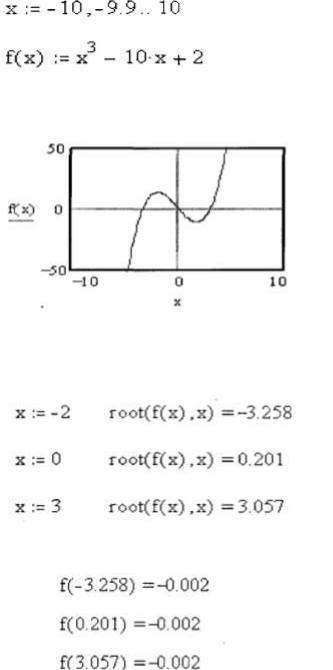
Например. Необходимо найти корни уравнения на заданном интервале
1.В окно MathCAD вводим исходные данные
2.Строим график левой части уравнения – функции
3.Используя три начальных приближения, определенных по графику находим корни уравнения
4.Осуществляем проверку
Функция POLYROOTS используется для нахождения корней полинома степени n. Формат: polyroots(v). Вектор v содержит коэффициенты полинома
Пример: найти корни полинома x3-10x+2

Решение при помощи функции polyroots
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Запустите интегрированную систему MathCAD
2.Выполните примеры 1 - 4
3.Выполните самостоятельное задание в соответствии с вариантом
Пример 1.
Требуется получить таблицу значений функции f (x) |
x |
на интервале |
|
||
1 x 2 |
[a,b] с шагом h.
Решение. Решение задачи можно свести к выполнению следующих шагов:
1.Определить функцию f(x).
2.Задать a, b, h.
3.Задать переменную (например, t), принимающую значение из промежутка на интервале [a, b] с шагом h.
4.Получить таблицу значений функции для переменной t.
5.На рис.3 представлен фрагмент документа с решением задачи.

Рис.3. Получение таблицы значений функции на заданном интервале с постоянным шагом
Пример 2. Построение графика в декартовой системе координат.
3становите курсор в том месте документа, где должен находиться график, и
вставьте шаблон декартова графика с помощью соответствующей кнопки на панели инструментов Графики.
Шаблон содержит 2 поля ввода. В поле ввода, расположенное возле оси ординат, введите нужную функцию (например, 2sin(x)), а в поле ввода,
расположенное возле оси абсцисс, имя аргумента функции (в данном случае, x).
Если после этого щелкнуть на рабочей области документа где-нибудь вне графика, то график будет построен.
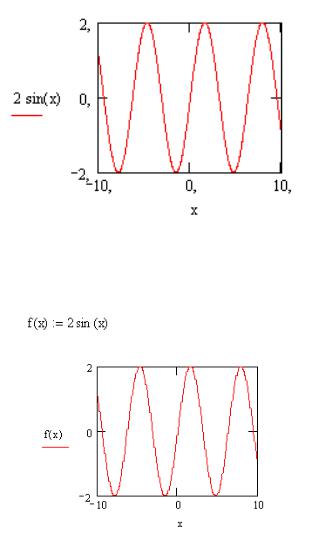
Функцию можно задать до построения графика, а в поле ввода функции ввести ее название:
Пример 3. Постройте график в полярной системе координат в соответствии с рисунком. Для построения двух линий в одном поле графика, введите имена функций через запятую.

Пример 4. Найти корни уравнения на заданном интервале
1.В окно MathCAD вводим исходные данные
2.Строим график левой части уравнения – функции
3.Используя три начальных приближения, определенных по графику находим корни уравнения
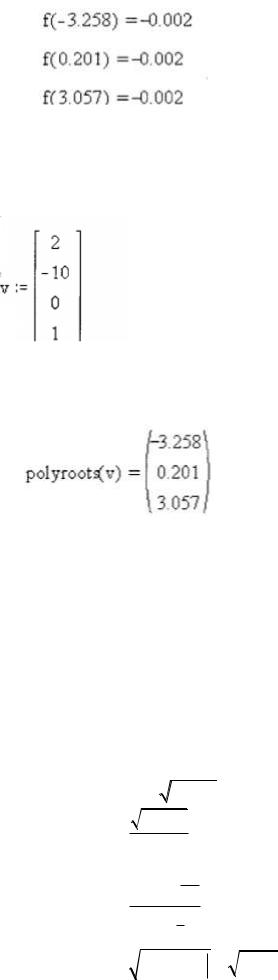
4. Осуществляем проверку
Функция POLYROOTS используется для нахождения корней полинома степени n. Формат: polyroots(v). Вектор v содержит коэффициенты полинома
Пример: найти корни полинома x3-10x+2
Решение при помощи функции polyroots
ВАРИАНТЫ ЗАДАНИЯ
1. Рассчитать выражения в соответствии с вариантом, используя встроенные функции, вывести на экран вспомогательные слова. Получите таблицу значений функции на интервале [a, b] с шагом h. Ответ должен содержать m знаков после запятой; переменную x определить в соответствии с областью определения.
Построить график функции y(x).
Вариант 1
Вариант 2
Вариант 3
Вариант 4
y
y
y
y
1 sin 2 8 x3 |
, m = 4, a = –5, b = 5, h = 1. |
||||
3 |
|
|
|
||
8 x3 |
|||||
|
|||||
3 x 16 , m = 3, a = 10, b = 14, h = 0.5. lg 2 x
x 16 , m = 3, a = 10, b = 14, h = 0.5. lg 2 x
1 lg 2 x
10 , m = 2, a = 2, b = 8, h = 0.5.
x
1 e 2
4

 x 2 2,5 3
x 2 2,5 3
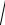 lg x 2 , m = 4, a = 10, b = 15, h = 1.
lg x 2 , m = 4, a = 10, b = 15, h = 1.

Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
|
|
|
|
2 x 3 x |
|
|
|
|
|
|
|
|||
y |
3 x , m = 3, a = 3, b = 8, h = 1. |
|||||||||||||
|
lg | |
2 |
| |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
y |
|
|
|
27 sin 2 3x |
||||||||||
|
|
|
|
|
, m = 2, a = –3, b = 2, h = 1. |
|||||||||
|
|
arccos 2x e x / 2 |
||||||||||||
y |
lg x 2 1 |
|||||||||||||
|
|
, m = 4, a = 4, b = 11, h = 1. |
||||||||||||
log 5 |
4x 2 9 |
|||||||||||||
y |
|
|
arccos x 2 |
25 |
||||||||||
|
|
|
|
, m = 3, a = –2, b = 3, h = 1. |
||||||||||
|
|
arcsin x 2 |
4 |
|||||||||||
y arcsin x 4 arccos x3 , m = 2, a = –5, b = 5, h = 1. |
||||||||||||||
y 5 x 2 1 lg x 2 1 3
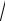 x 2 1 , m = 4, a = 5, b = 10, h = 1.
x 2 1 , m = 4, a = 5, b = 10, h = 1.
4 |
|
|
|
|
|
|
х+2 |
|
|||||
у = |
|
|
|
|
m = 3, a = 10, b = 14, h = 0.5. |
|
1−e2 |
||||||
6 |
|
|
|
|||
cos (х)+2 |
|
|||||
у = |
|
|
|
|
|
m = 3, a = 10, b = 14, h = 0.5. |
|
5 |
|
||||
|
|
|
|
|||
2. Построить графики заданных функций в декартовой системе координат заданным цветом с пересекающимися в начале координат осями и названием, не отображая выражения, задающие функции. Оба графика должны быть
изображены сплошной линией, но разной толщины.
1) |
f (x) x2 1, |
синий |
g(x) sin x , красный |
||||||||
2) |
f (x) |
x2 1 |
, |
зеленый |
|
g(x) cos x , черный |
|||||
|
|
x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
3) |
f (x) |
2 |
|
, |
голубой |
|
g(x) sin( x2 1) , коричневый |
||||
|
|
|
|
|
|||||||
|
|
x2 1 |
|
|
|
|
|
||||
4) |
f (x) |
x 1 |
|
, фиолетовый |
g(x) 2x 1 , красный |
||||||
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
5) |
f (x) x2 2 , |
зеленый |
|
g(x) ln x , голубой |
|||||||
6) |
f (x) x3 1, |
коричневый |
g(x) sin( x 3) , красный |
||||||||
7) |
f (x) x3 2 , |
синий |
g(x) cos(x 3) , черный |
||||||||
8) |
f (x) 3 (x3 |
2) , фиолетовый |
g(x) cos2 (x 1) , голубой |
||||||||
9) |
f (x) 2 (x3 1) , синий |
g(x) sin2 (x 1) , зеленый |
|||||||||
|
|
2 |
|
|
|
|
|
g(x) ln x , красный |
|||
10) |
f (x) |
|
, голубой |
|
|||||||
x2 1 |
|
||||||||||
11) |
f (x) x3 1, коричневый |
|
g(x) sin2 (x 1) , зеленый |
||||||||
