
Иксис Пр Работы / Отчет по Пр 2
.pdfМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра информационных систем
Отчет по практической работе №2 по дисциплине “Инфокоммуникационные системы и сети”
Тема: Множественный доступ: алгоритмы и временные диаграммы Вариант 154
Студент гр. 2376 |
_____________________ |
Федорков Ю.А. |
Преподаватель |
______________________ |
Воробьев А.И. |
Санкт-Петербург
2024
1 часть
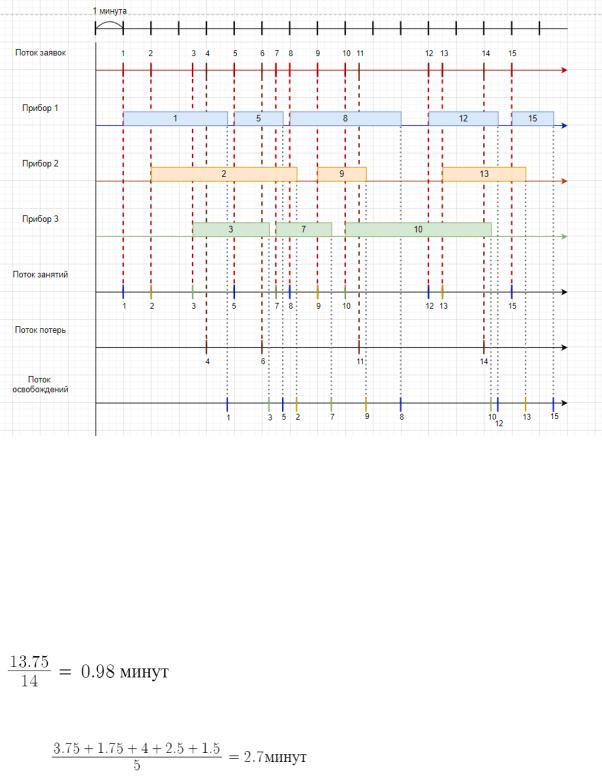
1. Построить временную диаграмму (1-ая временная диаграмма) обслуживания 15 заявок СМО G/G/3 по примеру слайда 16 из презентации 02_2. Временная диаграмма не должна повторять временные диаграммы других студентов группы. На временной диаграмме отметить моменты событий, связанные с потерями заявок, занятиями и освобождениями обслуживающих приборов.
2. По построенной временной диаграмме рассчитать средние времена: - интервалов времени между поступившими заявками, - занятости каждого из 3-х приборов и произвольного прибора, - между моментами занятий, потерь и освобождений. Для измерения времен протекания процессов считать, что 1-й минуте системного времени соответствует ширина клеточки в 1 см.
Среднее время интервалов между заявками:
Среднее время занятости прибора №1, №2, №3:
1)
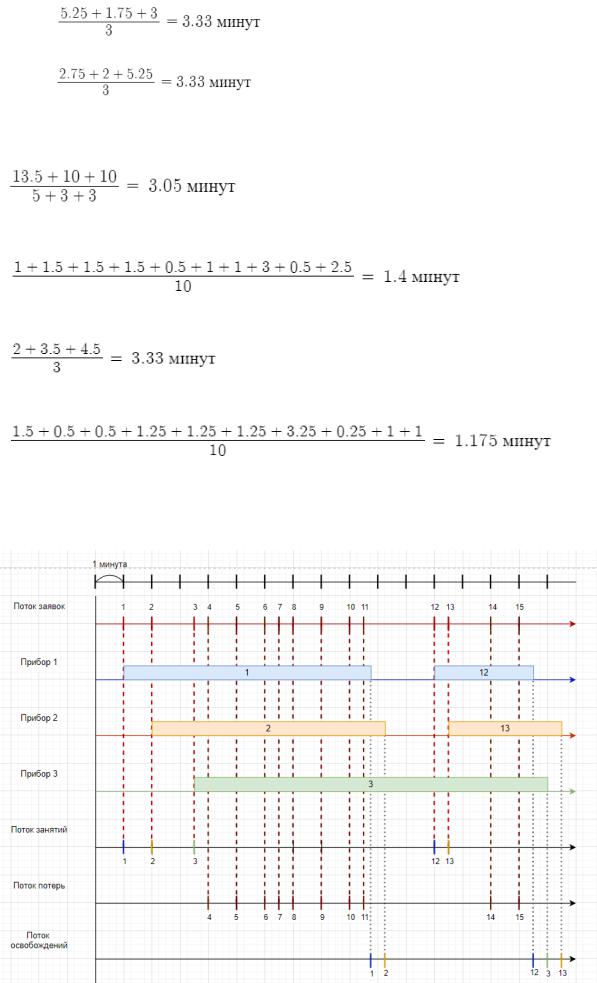
2)
3)
Среднее время занятости произвольного прибора:
Среднее время между моментами занятий приборов:
Среднее время между интервалами потерь заявок:
Среднее время между моментами освобождений:
3. Построить временную диаграмму (2-ая временная диаграмма), изменив уже построенную ранее (1-ую временную диаграмму) таким образом, чтобы было потеряно ровно 10 заявок из 15 поступивших.

Среднее время интервалов между заявками:
Среднее время занятости прибора №1, №2, №3: 1)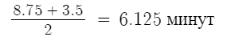 2)
2)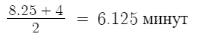 3)
3)
Среднее время занятости произвольного прибора:
Среднее время между моментами занятий приборов:
Среднее время между интервалами потерь заявок:
Среднее время между моментами освобождений:
4. Изменить СМО G/G/3 на G/G/3/2. Построить временную диаграмму (3- я временная диаграмма) по примеру слайда 17 из презентации 02_2, сохранив времена занятия приборов из 2-ой временной диаграммы (пункт 3 настоящего задания).
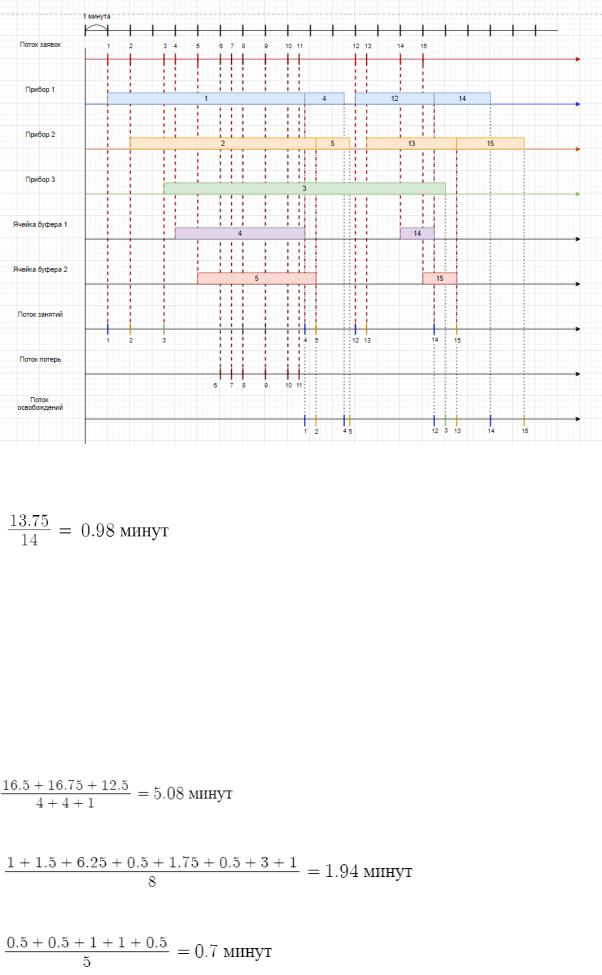
Среднее время интервалов между заявками:
Среднее время занятости прибора №1, №2, №3:
1)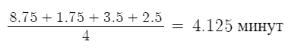
2) 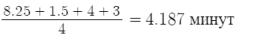
3) 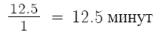
Среднее время занятости произвольного прибора:
Среднее время между моментами занятий приборов:
Среднее время между интервалами потерь заявок:

Среднее время между моментами освобождений:
Среднее время пребывания заявок в ячейках буфера №1 и №2: 1)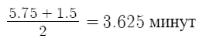
2)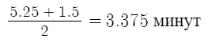
Среднее время пребывания заявки в очереди
5. Рассчитать те же средние времена, что и в пункте 2, для второй и третьей временных диаграмм, а также среднее время пребывания заявки в очереди – для третьей диаграммы.
(см.выше)
Часть 2
1. Построить графики функции и плотности трех экспоненциальных распределений. Параметры распределений каждому студенту вычислить по формулам:
μ1 ² = 154 μ2 ² = 308 μ3 ² = 462
Экспоненциальное распределение
Функция распределения вероятностей экспоненциального времени обслуживания:
( ) = 1 − −μ
Получаем функции:
1( ) = 1 − −1542( ) = 1 − −3083( ) = 1 − −462
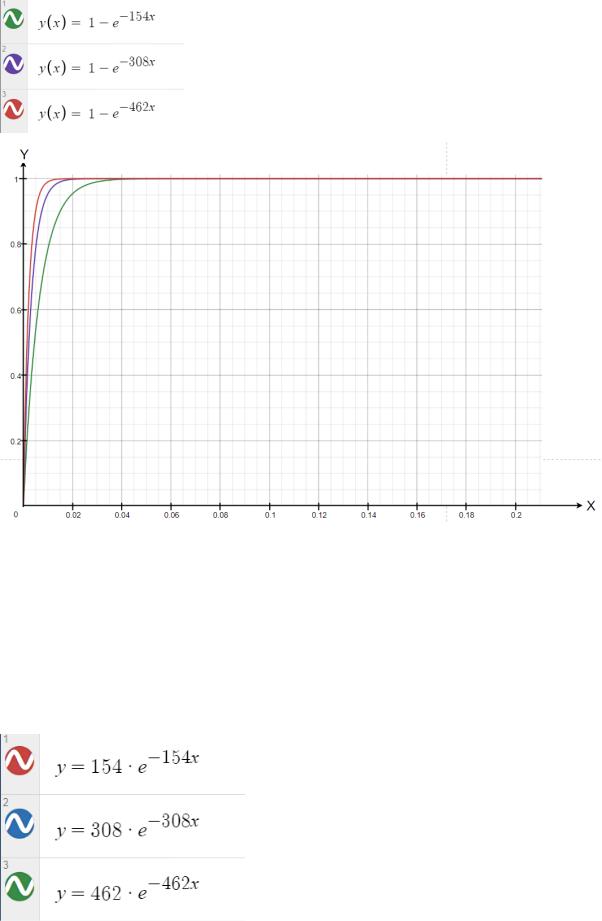
Функция плотности распределения вероятности
( ) = μ−μ
Получаем функции:
1( ) = 154−154
2( ) = 308−308
3( ) = 462−462
Построим график плотности распределения вероятностей:
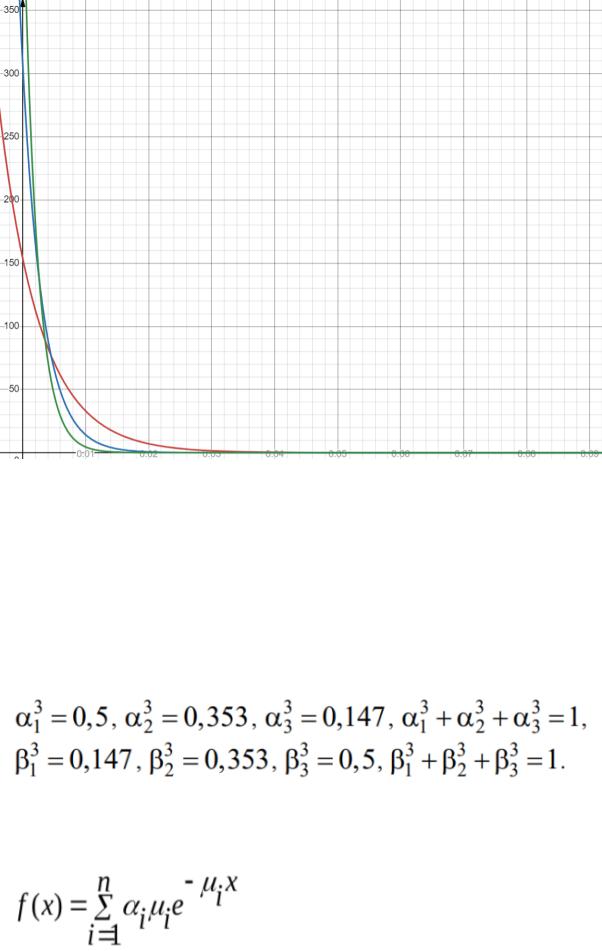
2. Построить графики плотности двух гиперэкспоненциальных распределений, полученных как аддитивная смесь из n = 3 экспоненциальных распределений. Принять следующие значения параметров. Интенсивности экспоненциальных распределений для обоих гиперэкспоненциальных распределений: где интенсивности, вычисленные в п. 2 настоящего задания. Весовые коэффициенты экспоненциальных распределений для первого и второго гиперэкспоненциальных распределений, соответственно:
Гиперэкспоненциальное распределение
Формула плотности гиперэкспоненциального распределения:
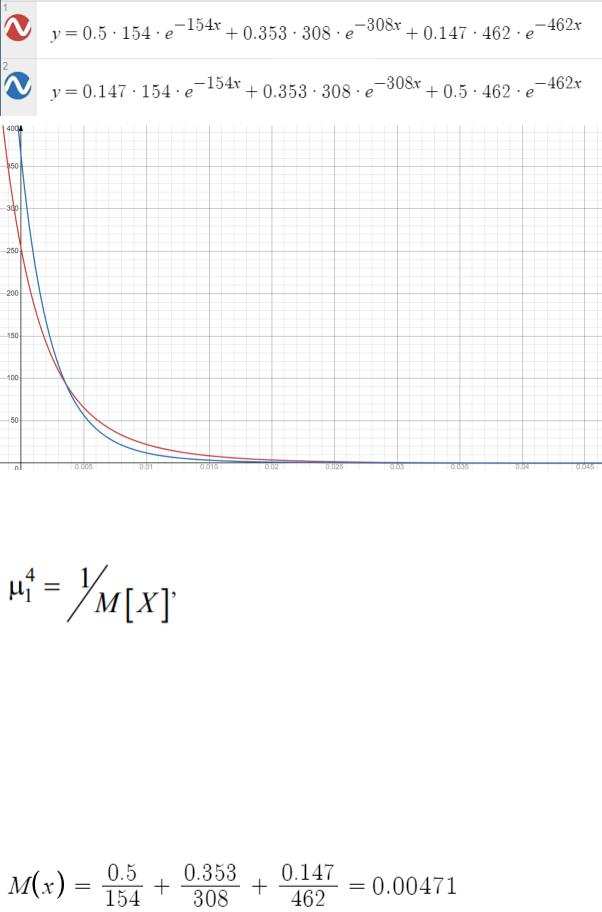
Построим график плотности распределения гиперэкспоненциального распределения:
3. В этих же осях, что и графики п. 3, построить график плотности
экспоненциального распределения со значением интенсивности 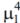 , вычисленной по формуле:
, вычисленной по формуле:
где 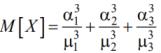 математическое ожидание экспоненциального распределения.
математическое ожидание экспоненциального распределения.
Сделать вывод о том, при каких распределениях и каких значениях интенсивностей меньше вероятность больших значений случайных величин.
Вычислим математическое ожидание экспоненциального распределения
Получим значение 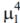 :
:
μ1 4 = 1/0. 00471 = 212
Формула плотности экспоненциального распределения 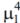 :
:
4( ) = 212 −212
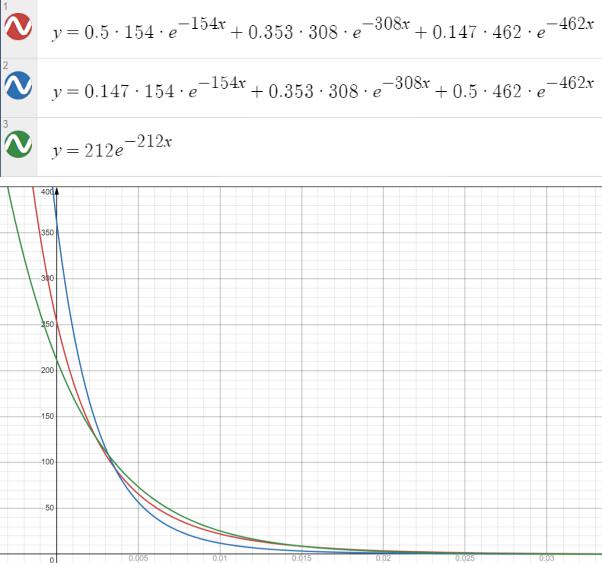
Построим график:
У гиперэкспоненциального распределения вероятность появления значений случайной величины меньших математического ожидания больше, чем у экспоненциального распределения. При гиперэкспоненциальном распределении вероятность появления больших значений при высокой интенсивности понижается с увеличением веса r и понижается при низкой интенсивности.
4. Построить графики плотности трех нормированных эрланговских распределений, отличающихся рангом:
