
Иксис Пр Работы / Отчет по Пр 2
.docxМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра информационных систем
Отчет по практической работе №2
по дисциплине “Инфокоммуникационные системы и сети”
Тема: Множественный доступ: алгоритмы и временные диаграммы
Вариант 154
Студент гр. 2376 _____________________ Федорков Ю.А.
Преподаватель ______________________ Воробьев А.И.
Санкт-Петербург
2024
1 часть
1. Построить временную диаграмму (1-ая временная диаграмма) обслуживания 15 заявок СМО G/G/3 по примеру слайда 16 из презентации 02_2. Временная диаграмма не должна повторять временные диаграммы других студентов группы. На временной диаграмме отметить моменты событий, связанные с потерями заявок, занятиями и освобождениями обслуживающих приборов.


2. По построенной временной диаграмме рассчитать средние времена: - интервалов времени между поступившими заявками, - занятости каждого из 3-х приборов и произвольного прибора, - между моментами занятий, потерь и освобождений. Для измерения времен протекания процессов считать, что 1-й минуте системного времени соответствует ширина клеточки в 1 см.
Среднее время интервалов между заявками:

Среднее время занятости прибора №1, №2, №3:
Среднее время занятости произвольного прибора:
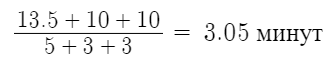
Среднее время между моментами занятий приборов:
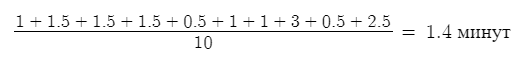
Среднее время между интервалами потерь заявок:
![]()
Среднее время между моментами освобождений:
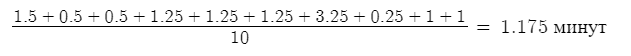
3. Построить временную диаграмму (2-ая временная диаграмма), изменив уже построенную ранее (1-ую временную диаграмму) таким образом, чтобы было потеряно ровно 10 заявок из 15 поступивших.

Среднее время интервалов между заявками:
Среднее время занятости прибора №1, №2, №3:
1)![]()
2)![]()
3)![]()
Среднее время занятости произвольного прибора:
![]()
Среднее время между моментами занятий приборов:

Среднее время между интервалами потерь заявок:
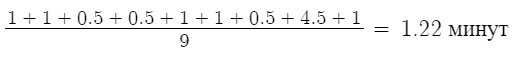
Среднее время между моментами освобождений:
![]()
4. Изменить СМО G/G/3 на G/G/3/2. Построить временную диаграмму (3- я временная диаграмма) по примеру слайда 17 из презентации 02_2, сохранив времена занятия приборов из 2-ой временной диаграммы (пункт 3 настоящего задания).

Среднее время интервалов между заявками:
Среднее время занятости прибора №1, №2, №3:
1)
2)
![]()
3)
Среднее время занятости произвольного прибора:
![]()
Среднее время между моментами занятий приборов:

Среднее время между интервалами потерь заявок:
![]()
Среднее время между моментами освобождений:
![]()
Среднее время пребывания заявок в ячейках буфера №1 и №2:
1)![]()
2)![]()
Среднее время пребывания заявки в очереди
![]()
5. Рассчитать те же средние времена, что и в пункте 2, для второй и третьей временных диаграмм, а также среднее время пребывания заявки в очереди – для третьей диаграммы.
(см.выше)
Часть 2
1. Построить графики функции и плотности трех экспоненциальных распределений. Параметры распределений каждому студенту вычислить по формулам:
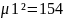
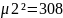
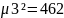
Экспоненциальное распределение
Функция распределения вероятностей экспоненциального времени обслуживания:
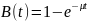
Получаем функции:
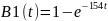
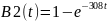
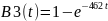
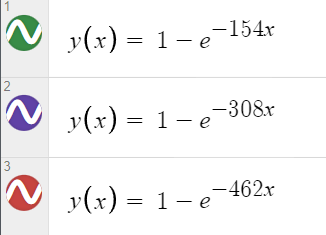
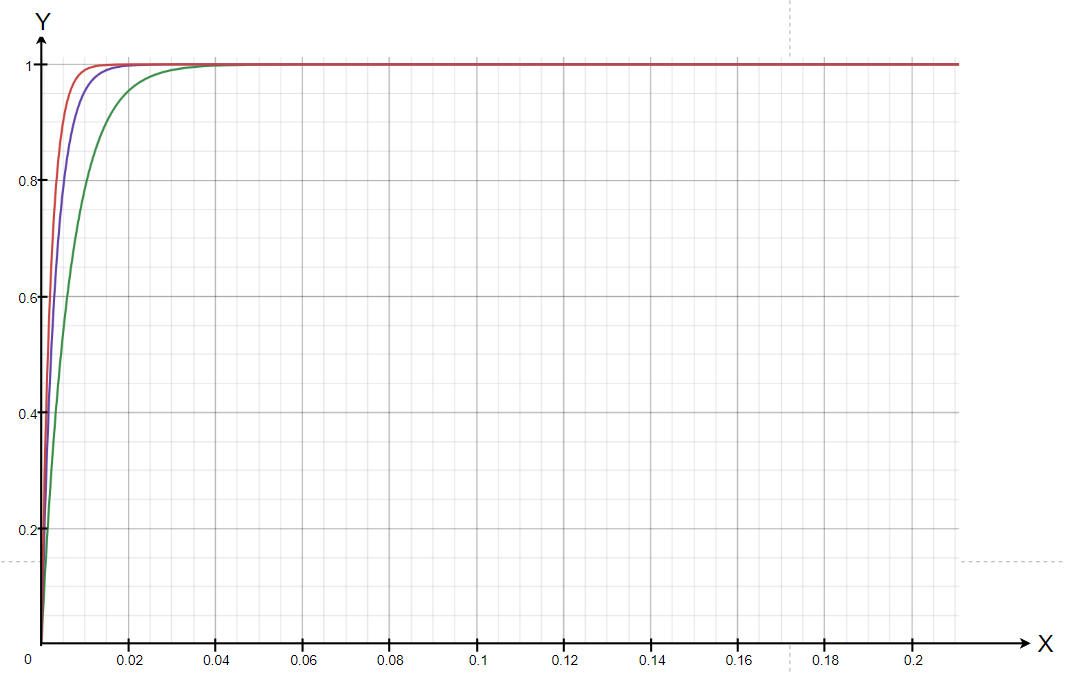
Функция плотности распределения вероятности
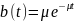
Получаем функции:
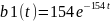
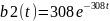
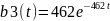
Построим график плотности распределения вероятностей:
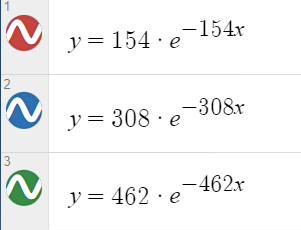

2. Построить графики плотности двух гиперэкспоненциальных распределений, полученных как аддитивная смесь из n = 3 экспоненциальных распределений. Принять следующие значения параметров. Интенсивности экспоненциальных распределений для обоих гиперэкспоненциальных распределений: где интенсивности, вычисленные в п. 2 настоящего задания. Весовые коэффициенты экспоненциальных распределений для первого и второго гиперэкспоненциальных распределений, соответственно:
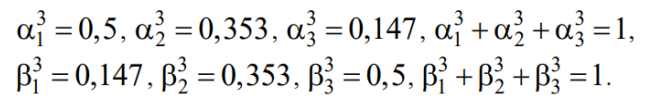
Гиперэкспоненциальное распределение
Формула плотности гиперэкспоненциального распределения:

Построим график плотности распределения гиперэкспоненциального распределения:

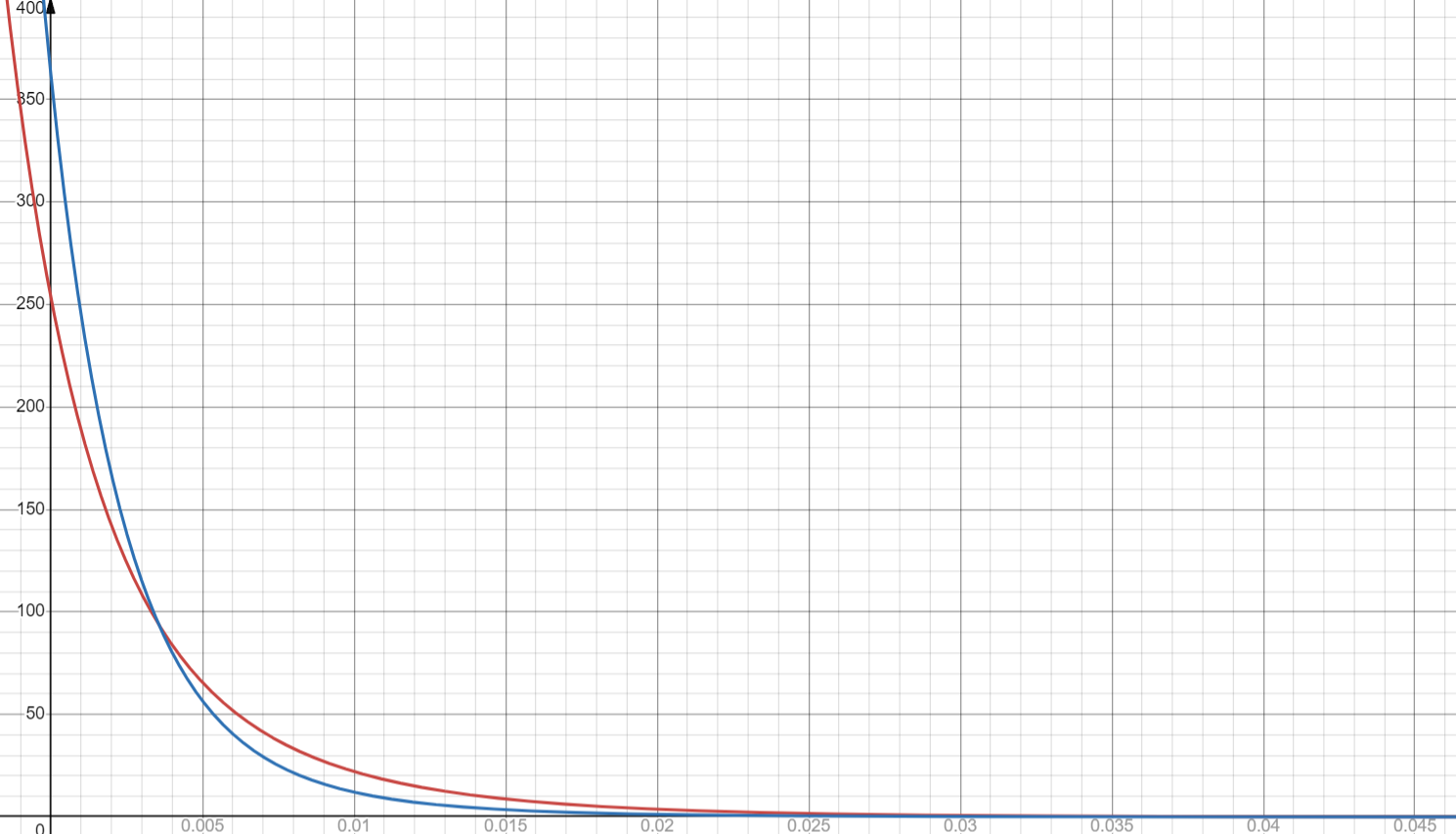
3.
В этих же осях, что и графики п. 3, построить
график плотности экспоненциального
распределения со значением интенсивности
![]() ,
вычисленной по формуле:
,
вычисленной по формуле:

где
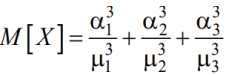 математическое
ожидание экспоненциального распределения.
математическое
ожидание экспоненциального распределения.
Сделать вывод о том, при каких распределениях и каких значениях интенсивностей меньше вероятность больших значений случайных величин.
Вычислим математическое ожидание экспоненциального распределения
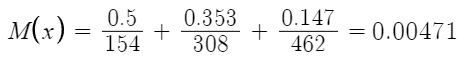
Получим значение :
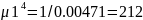
Формула плотности экспоненциального распределения :
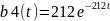
Построим график:

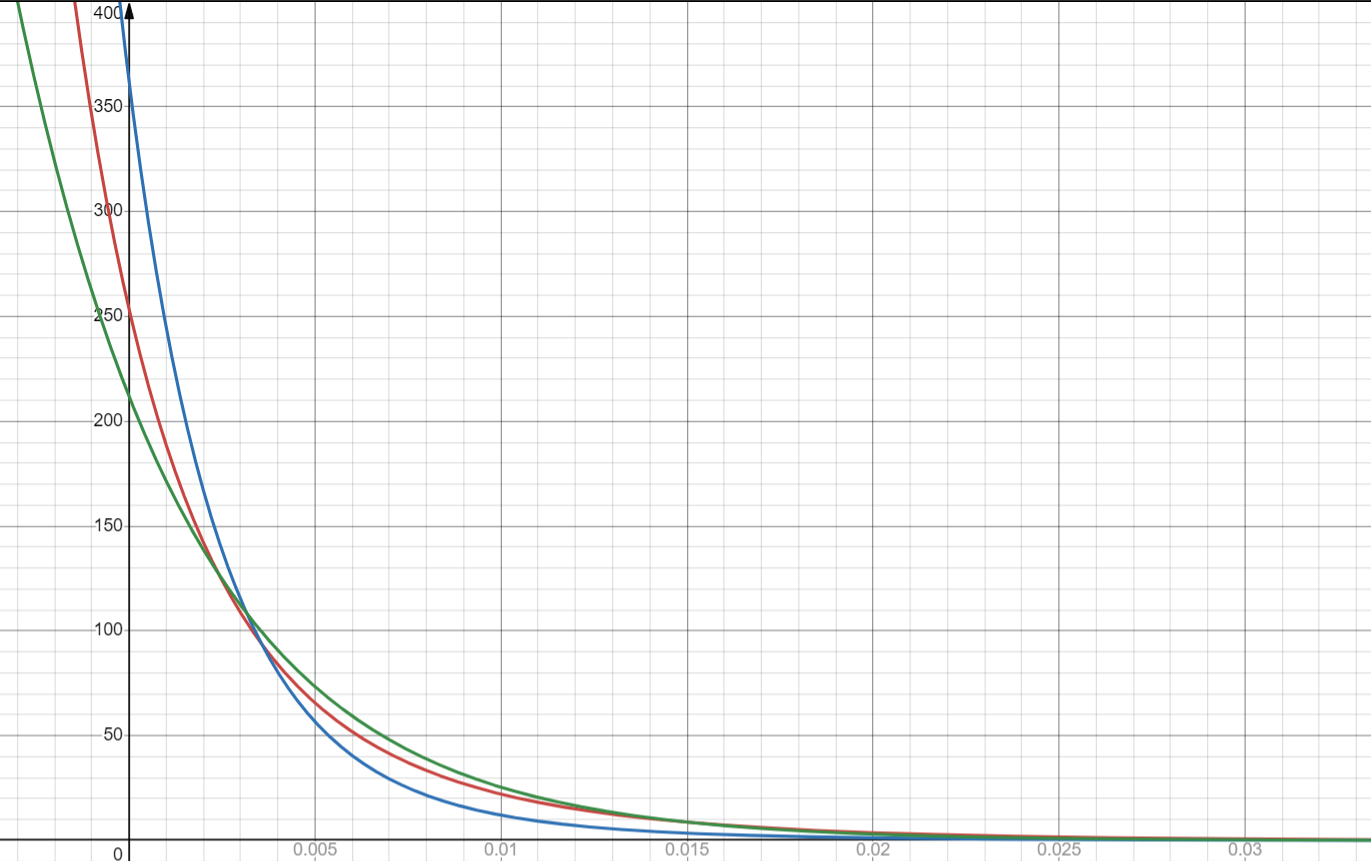
У гиперэкспоненциального распределения вероятность появления значений случайной величины меньших математического ожидания больше, чем у экспоненциального распределения. При гиперэкспоненциальном распределении вероятность появления больших значений при высокой интенсивности понижается с увеличением веса r и понижается при низкой интенсивности.
4. Построить графики плотности трех нормированных эрланговских распределений, отличающихся рангом:

Интенсивности для этих трех распределений вычислить по формулам:
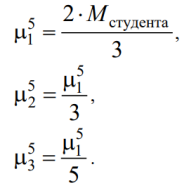
Сделать вывод об изменении плотности распределения по мере увеличения ранга r.
Нормированное эрланговское распределение
Плотность эрланговского распределения

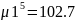
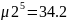
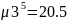
Построим график плотности эрланговского распределения
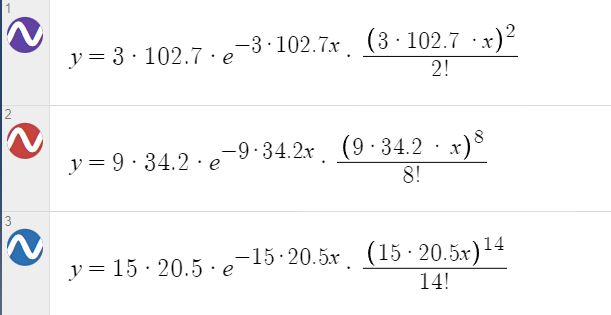
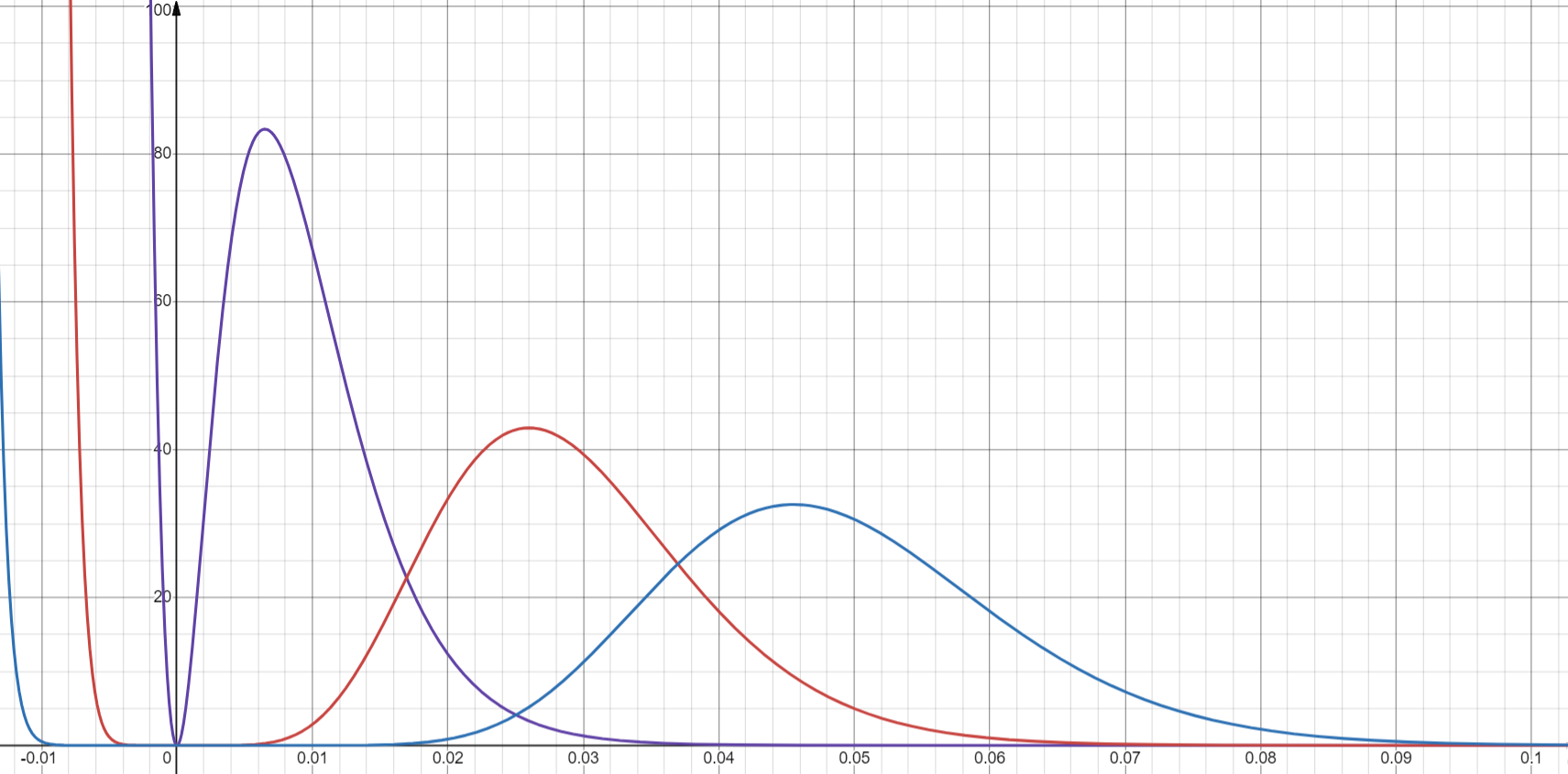
По мере увеличения ранга пик плотности распределения поднимается. По мере уменьшения интенсивности пик становится ниже, шире и смещается в сторону больших значений t.
Выводы:
Таким образом, в первой части работы были рассмотрены случаи с обслуживанием заявок СМО G/G/3, с большим и малым количеством потерь, а также случай с СМО G/G/3/2. Из построенных временных диаграмм и рассчитанных значений видно, что добавление очередей значительно снижает возможное число потерь заявок, которые возникают вследствие долгого обслуживания приборами.
Во второй части работы были построены графики для экспоненциальных, гиперэкспоненциальных и нормированных эрланговских распределений с различными параметрами. По графикам были сделаны выводы о влиянии на вероятности различных параметров интенсивности и рангов .
