лаба 3.2

САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа № 3.2

"Измерение расхода газа методом отсеченного объема"

Студент гр. 3231401/20001 Школьников А.С.

Сирош С.А.

Преподаватель Павлов А.В.

Введение

Данная работа проведена для измерения массового расхода методом отсеченного объема. Метод отсеченного объема основан на уравнении Менделеева-Клапейрона. Также в данной работе вычисляется неопределенность измерения массового расхода.

Описание установки

Экспериментальная установка представляет из себя стенд (рис.1). Сам стенд подключен к источнику тока и состоит из: компрессора (1), ресивера для сжатого воздуха (5), датчика температуры (2), датчика давления (3), для безопасности используется предохранительный клапан (4).

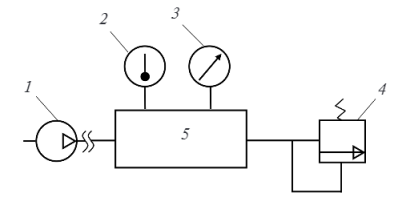
Рисунок 1. Схема воздушного контура

Ход работы:

1. Включаем питание стенда

2. Снимаем показания температуры ( ) и давления ( ) в ресивере, заносим их в таблицу 3.3

3. Запускаем компрессор и одновременно включаем секундомер

4. Дожидаемся пока в ресивере давление достигнет 100 кПа, выключаем одновременно компрессор и секундомер

5. Измеряем давление ( и температуру ( ) в ресивере и время по секундомеру, заносим результат в таблицу 3.3

6. Сбрасываем показания секундомера

7. Сбрасываем давление в ресивере при помощи клапана

8. Повторяем пункты 2-6 для 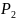=125 кПа и =150 кПа

Результаты эксперимента

Таблица 3.3

№	, кПа	, °C	, кПа	, °C	τ, c
1	0	22,5	100	22,9	24,84
2	0	22,8	127	23,6	31,26
3	0	23,1	151	23,8	38,38

Показания приборов

Обработка результатов

Метод отсеченного объема – метод измерения расхода идеального газа по падению давления в емкости, основанный на уравнении Менделеева-Клапейрона: PV=MRT, где P – давление газа, Па; V – объем, занимаемый газом,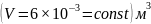 ; M – масса газа, кг; T – абсолютная температура газа, К; R – газовая постоянная, .

По уравнению Менделеева-Клапейрона, масса газа в начальный момент времени: , кг, где – абсолютное давление газа в начальный момент времени, Па, – абсолютная температура газа в начальный момент времени, К, – молярная масса газа ( =0,029 кг/моль). Масса газа после нагнетания: 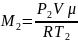, кг, где – абсолютное давление газа после сжатия воздуха, Па, – абсолютная температура воздуха после сжатия. Расход газа: , кг/с.

В начальный момент времени массы газов в опытах соответственно равны:

1. кг

2. кг

3. кг

Массы газа после сжатия воздуха в опытах соответственно равны:

1. кг

2. кг

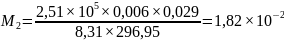3. кг

Массовый расход для каждого опыта равен соответственно:

1. кг/с

2. кг/с

3. кг/с

Неопределенность измерений массового расхода вычисляется по формуле: , где - неопределенность измерения массы газа; – неопределенность измерения времени ( .

Где – неопределенность измерения давления; – неопределенность измерения температуры.

, где – неопределенность отсчета измеряемой величины P ( ), %; – неопределенность полного диапазона измерений M, ( %, ( = Па).

Рассчитаем неопределенность измерения давления для каждого опыта:

1. Па

2. Па

3. Па

, где К

Рассчитаем неопределенность измерения температуры для каждого опыта:

1. К

2. К

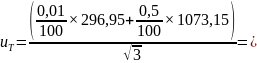3. 3,12 К

Рассчитаем неопределенность измерения массы газа для каждого опыта:

1. = =1,44 кг

2. = =1,44 кг

3. = =1,44 кг

Рассчитаем неопределенность измерения массы газа для каждого опыта:

1. = =1,93 кг

2. = =2,08 кг

3. = =2,23 кг

Рассчитаем неопределенность измерений массового расхода для каждого опыта:

1. 

Построим график зависимости массового расхода G от разности давлений p2 и p1(рис.2):

Рисунок 2 - Зависимость массового расхода от разности давлений

Вывод

Графическая зависимость массового расхода от разности давлений показывает, что с увеличением разности давлений увеличивается расход. Заметим также, что рассчитанные значения неопределенностей свидетельствуют о том, что точность измерений с повышением разности давлений и, соответственно, массового расхода становится выше. Получаем, что данный метод наиболее эффективен при измерение больших величин. Но стоит заметить, что метод отсеченного объема основан на уравнение Менделеева-Клапейрона для идеального газа, но воздух таковым не является.

Санкт-Петербург

2022