
Интегрирование тригонометрических функций
.pdf
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§5 Интегрирование тригонометрических функций

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
Рассмотрим интегралы, которые часто применяются на практике
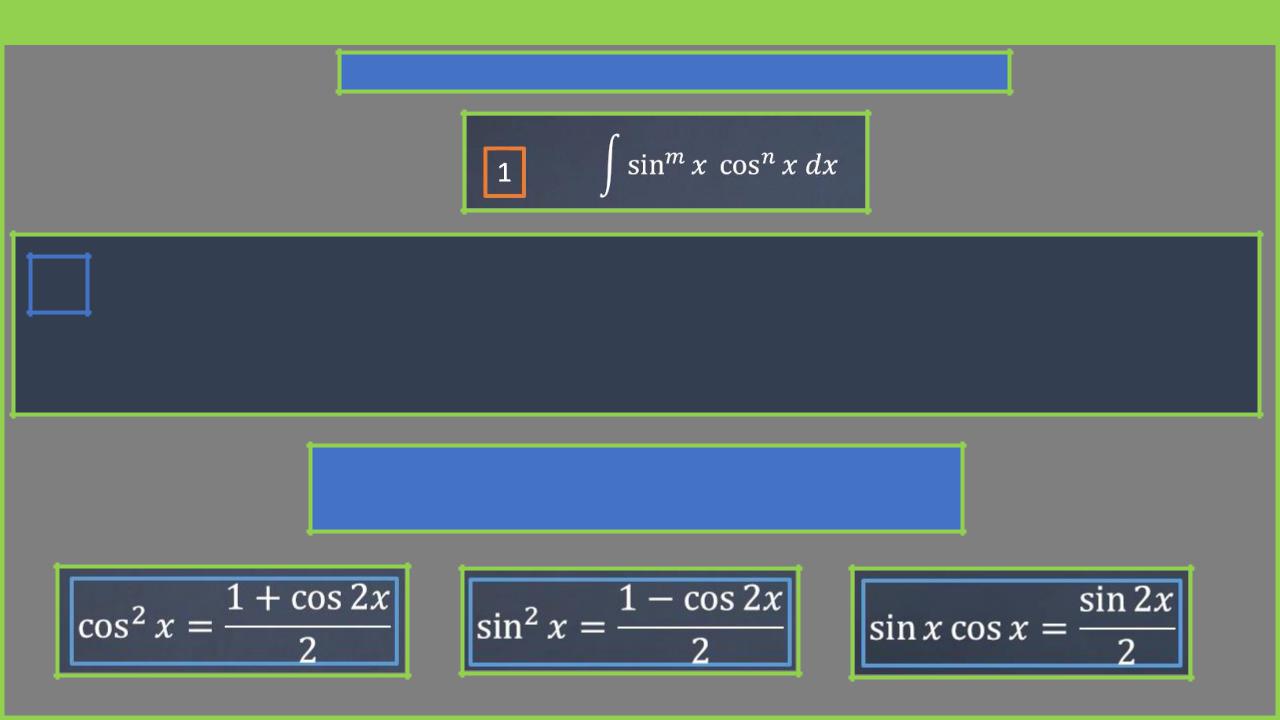
1) |
m − нечетноеположительное, |
т.е. хотя бы одно из значений m или принимает |
|
− нечетноеположительное |
|
нечетное положительное значение или ноль
|
|
Делается замена переменной: |
||
|
если m − нечетное, то sin = |
cos = |
||
|
если − нечетное, то cos = −sin = |
|||
|
|
|
|
|
|
|
Здесь замену можно не делать, а использовать |
|
|
Замечание |
|
метод подведение под знак дифференциала: |
|
|
|
cos = ; sin = − cos |
|
||
|
|
|
||
|
|
|
|
|

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
Пример
Здесь = 3, поэтому можно сделать замену cos = −sin = или использовать метод подведение под знак дифференциала
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
m− четное положительное (или 0)
2)− четное положительное (или 0), т.е. оба значения m и принимают четное
положительное значение или одно из них равно 0.
Используем формулы понижения степени:

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
1. |
Примеры
2. |

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
|
|
|
Делается замена переменной: |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
tg = |
2 = или |
ctg = − |
2 |
= |
|
|
|
|
|
|
||||
|
|
Здесь замену можно не делать, а использовать метод |
|
||||
|
|
подведение под знак дифференциала: |
|
|
|
||
Замечание |
|
1 |
1 |
|
|
|
|
|
|
|
2 = |
tg ; 2 = − (ctg ) |
|
||
|
|
|
|
|
|
|
|

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
Пример

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
Используем формулы :
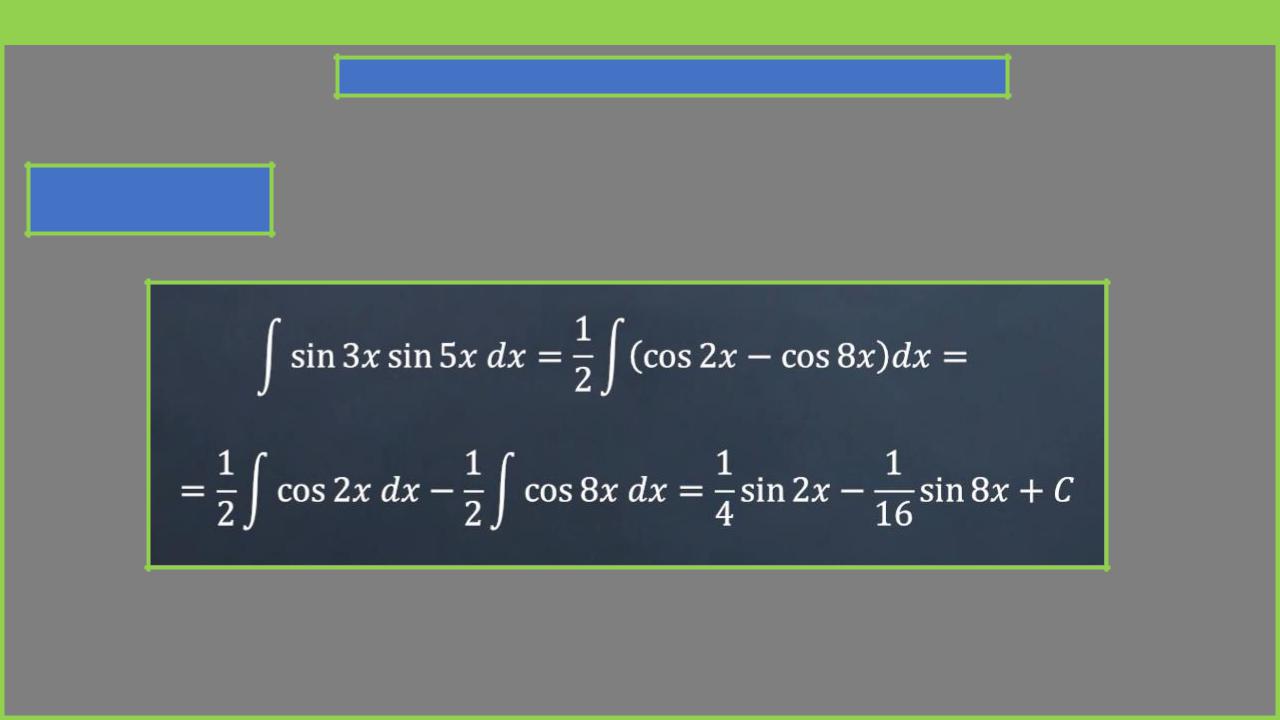
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
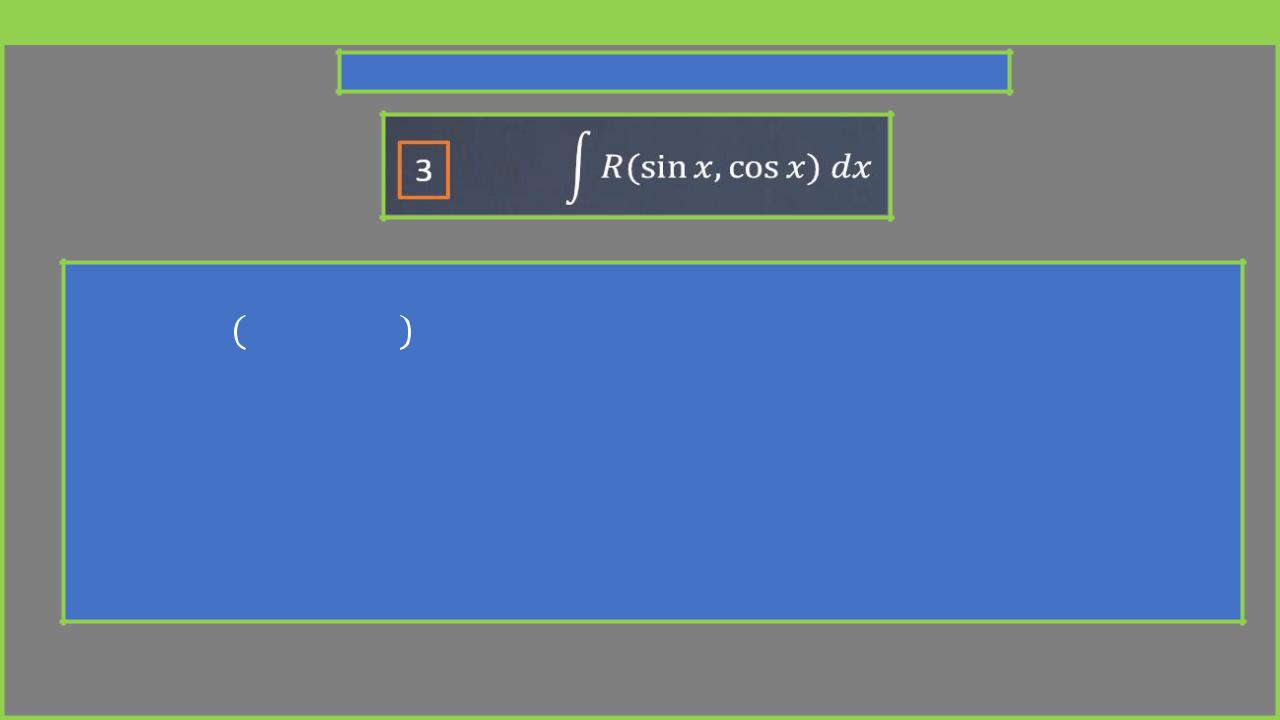
Пример
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегрирование тригонометрических функций
Здесь sin , cos – функция, рационально зависящая от аргументов sin , cos . Это означает, что для нахождения значения функции над аргументами производятся только 4 арифметических действия.
Для отыскания интегралов такого вида можно применить 4 типа подстановок, которые сводят интеграл к интегралу от рациональной функции нового аргумента t :
