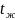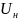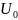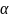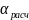САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа ТМО – 2.4

"Теплообмен при пузырьковом кипении жидкости"

Студент гр. 3231401/20002 ______Школьников А.С.

Студент гр. 3231401/20002 ______Сирош С.А.

Преподаватель ________________ Павлов А. В.

Содержание

1. Введение 3

2. Описание установки 6

3. Результаты эксперимента 6

5. Вывод 10

1. Введение

Кипение - процесс перехода вещества из жидкого агрегатного состояния в газообразное. Обязательным условием для кипения является перегрев по всему объему или у поверхности нагрева. Если жидкость перегрета по всему объему, то возникает объёмное кипение. Оно наблюдается при разгерметизации контуров энергоустановок или других объектов, в которых имеется нагретая жидкость под давлением. Объемное кипение не поддается регулировке, что приводит к аварийным ситуациям.

Поверхностное кипение - упорядоченный процесс, который реализуется в котлах, бойлерах и других энергоустановках. В этом случае тепловой поток подводится со стороны поверхности, нагретой выше температуры насыщения. На поверхности возникают пузырьки пара, они растут, достигают отрывного диаметра и всплывают, затем на их месте возникают новые и процесс повторяется. На каждой стадии (возникновение, рост, отрыв и всплытие пузырька) коэффициент теплоотдачи а определяется разными факторами и потому может заметно меняться.

При исследовании кипения особая роль отводится эксперименту, и большинство расчетных формул по теплоотдаче при кипении основано на экспериментальных данных. Впервые эти данные обобщил в 1934 году Широ Нукияма в своей работе «Максимальное и минимальное количество тепла Q, переданного металлом кипящей воде при атмосферном давлении». Он построил зависимость плотности теплового потока от температурного напора ∆𝑇 = 𝑇с−𝑇н, где 𝑇с - температура стенки, 𝑇н – температура насыщения.

В областях А и В кипение только развивается, наблюдаются отдельные пузыри. В области С развитое пузырьковое кипение, с регулярным образованием, отрывом и всплытием отдельных пузырей. Увеличение температурного напора приводит к частичному оттеснению жидкости от нагретой поверхности. Пузыри объединяются, и часть разогретой поверхности теряет контакт с жидкостью, что приводит к резкому уменьшению плотности теплового потока и увеличению температуры поверхности нагрева (область Е). Этот процесс лавинообразный, вскоре вся поверхность нагрева покрывается паровой пленкой и начинается развитое пленочное кипение. Точку перехода от пузырькового кипения при повышении температурного напора к пленочному называют первой критической плотностью теплового потока.

В работе будет рассмотрен только режим пузырькового кипения (область С). При пузырьковом кипении паровые пузыри возникают в отдельных местах поверхности нагрева - центрах парообразования. Вырастая до определенного размера, паровые пузыри отрываются и всплывают в толще 3 жидкости. При этом перегрев основной массы жидкости весьма невелик (0,01 .. 0,1 °C).

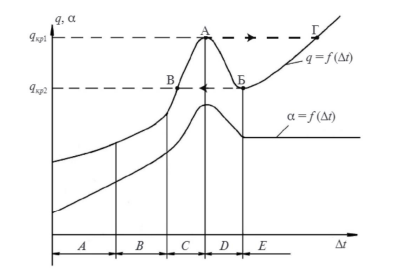
Рисунок 1 – Зависимость плотности теплового потока и коэффициента теплоотдачи

Результаты многочисленных экспериментальных исследований пузырькового кипения при умеренных тепловых потоках удовлетворительно обобщаются зависимостью:

,

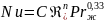Где ; ( ); ; ( ); ;

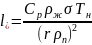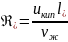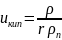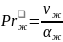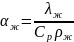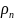; – удельная изобарная теплоемкость воды, Дж/кг/К; и – плотности насыщенной жидкости и сухого насыщенного пара соответственно, кг/м³; σ – коэффициент поверхностного натяжения, Н/м; r – скрытая теплота парообразования, Дж/кг; q – плотность теплового потока на поверхности нагрева, Вт/м²; 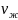– кинематическая вязкость жидкости, м/с² ; – теплопроводность жидкости, Вт/м/К; 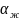– температуропроводность жидкости.

Эмпирические константы в уравнении выше принимают следующие значения: C = 0,0625, n = 0,5 (при 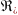≤ 0,01); C = 0,125, n = 0,65 (при ≥ 0,01).

Для расчета теплоотдачи при кипении воды можно воспользоваться более простыми соотношениями:

;

,

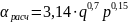где давление задается в барах, удельный тепловой потов в Вт/м²; перегрев жидкости – в К или °C.

Это относится к процессу кипения в большом объеме:

- когда размеры области нагрева и диаметр пузырьков намного меньше размера сосуда, в котором происходит кипение;

- когда жидкость не движется вдоль поверхности нагрева. Нарушение этих условий (например, при кипении в трубах) влияет на теплообмен и коэффициент теплоотдачи.

2. Описание установки

Лабораторная установка представлена на рисунке 2.

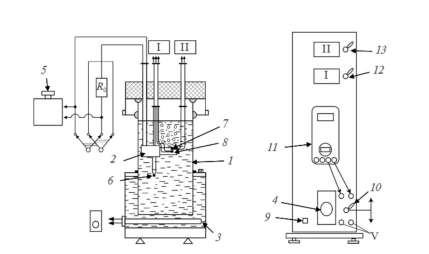
Рисунок 2– Лабораторная установка для изучения пузырькового кипения

1 – стеклянная емкость; 2 – экспериментальная модель; 3 – нагреватель; 4 – диммер; 5 – трансформатор; 6, 7, 8 – термопары; 9 – тумблер электропитания; 10 – тумблер сопротивления; 11 – мультиметр; 12, 13 –тумблеры выключения измерителей температуры.

3. Результаты эксперимента

Таблица 1

Результаты измерений

Номер опыта						Q
	°C			В			Вт
1	95,4	104,1	115		0,072	82,8
2	96,7	104,2	130		0,083	107,9
3	96,9	104,6	145		0,092	133,4

4. Обработка результатов

Определим тепловой поток по мощности, выделяющейся на нагревателе цилиндра:

,

где – падение напряжения на нагревателе цилиндра, В; – падение напряжения на образцовом сопротивлении 𝑅0, В.

Рассчитаем средний коэффициент теплоотдачи по поверхности нагретого цилиндра к кипящей воде:

, ,

где F – площадь поверхности цилиндра, м².

Рассчитаем значение коэффициента теплоотдачи по формуле с эмпирическими коэффициентами:

,

Таблица 2

Результаты расчетов

Номер опыта
	Вт/м²/К	Вт/м²	Бар	Вт/м²/К
1	1941	16895	1	2859
2	2935	22016	1	3442
3	3535	27219	1	3993

Оценим неопределенность измерений по формуле:

,

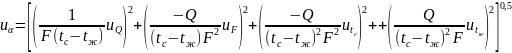где = 0,5 Вт, = 10-6 м 2; = = 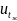0,5 К.

Результаты с учетом неопределенностей:

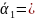1941 ± 158),

2935 ± 277),

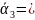3535 ± 324),

Рисунок 3 – График зависимости коэффициента теплоотдачи от плотности теплового потока

Рисунок 4 – График зависимости расчетного коэффициента теплоотдачи от плотности теплового потока

Рисунок 5 – График зависимости коэффициента теплоотдачи от плотности температурного напора

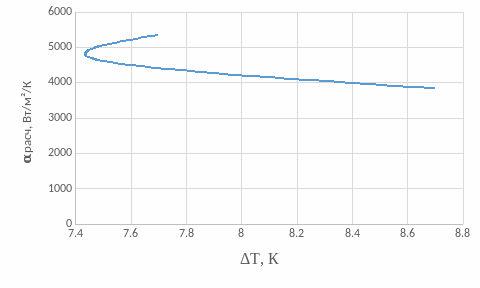
Рисунок 6 – График зависимости расчетного коэффициента теплоотдачи от температурного напора

5. Вывод

В данной лабораторной работе были сняты показания термопар жидкости в цилиндре и стенки, определены значения плотности теплового потока, коэффициенты теплоотдачи опытные и расчетные. Значения коэффициентов для одного опыта отличаются в 1,5 раза, что вероятно связано с некорректным определением площади поверхности теплообмена для формулы коэффициента теплоотдачи полученной из закона Ньютона– Рихмана.

Санкт-Петербург

2024