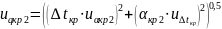САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа ТМО – 2.5

"Теплообмен при пленочном кипении"

Студент гр. 3231401/20002 ______Школьников А.С.

Студент гр. 3231401/20002 ______Сирош С.А.

Преподаватель ________________ Павлов А. В.

Содержание

1. Введение 3

2. Описание установки 5

3. Результаты эксперимента 5

5. Вывод 13

1. Введение

Пузырьковое кипение используется в подавляющем большинстве энергетических уставнок: оно сравнительно безопасно, этот процесс регулируется и обеспечивает плотность теплового потока меньше первой критической. Однако при повышении мощности нагрева, увеличивается температурный напор, и начинается пленочное кипение, при котором и начинается пленочное кипение, при котором коэффициент теплоотдачи почти не растет. Изменение плотности теплового потока не всех режимах кипения представлено на рисунке 1. Видно, что при пленочном кипении плотность теплового потока заметно возрастает – за счет теплообмена излучением – а температурный напор имеет порядок 10³ К, что недопустимо по соображением безопасности. Хуже всего то, что такой рост тепловой нагрузки занимает доли секунды, что ведет к катастрофическим последствиям.

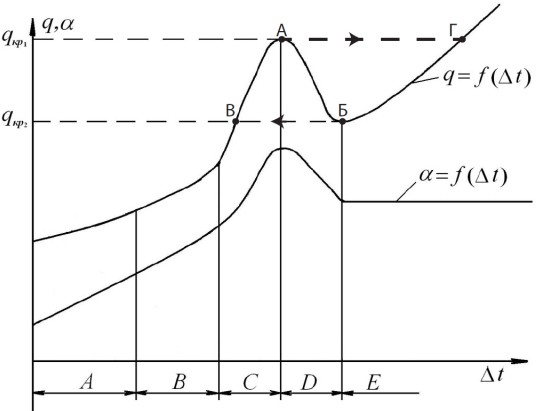
Рисунок 1 – Зависимость плотности теплового потока и коэффициента теплоотдачи от температурного напора.

Графики, представленные на рисунке 1 получены в ходе экспериментов, в которых температурный напор меняется медленно. В промышленных условиях после достижения точки А значение плотности теплового потока перескакивает мгновенно в точку Г, а следовательно, мгновенно возрастает до сотен градусов и температурный напор. Обратный процесс идет по Б–В.

В данной реализуется режим пленочного кипения. Согласно рис.1, после точки (Б), соответствующей второй критической плотности теплового потока , коэффициент теплоотдачи имеет малое значение и почти не зависит от плотности теплового потока.

В данной работе коэффициент теплоотдачи при пленочном кипении определяется методами теории регулярного теплового режима.

Массивная металлическая болванка нагревается до 350..400 , быстро погружается в воду, температура которой близка к температуре насыщения. Охлаждение болванки идет в среде с постоянной температурой, а коэффициент теплоотдачи, как показано на рис. 1, почти не меняется. Следовательно, наблюдается регулярный режим первого рода.

2. Описание установки

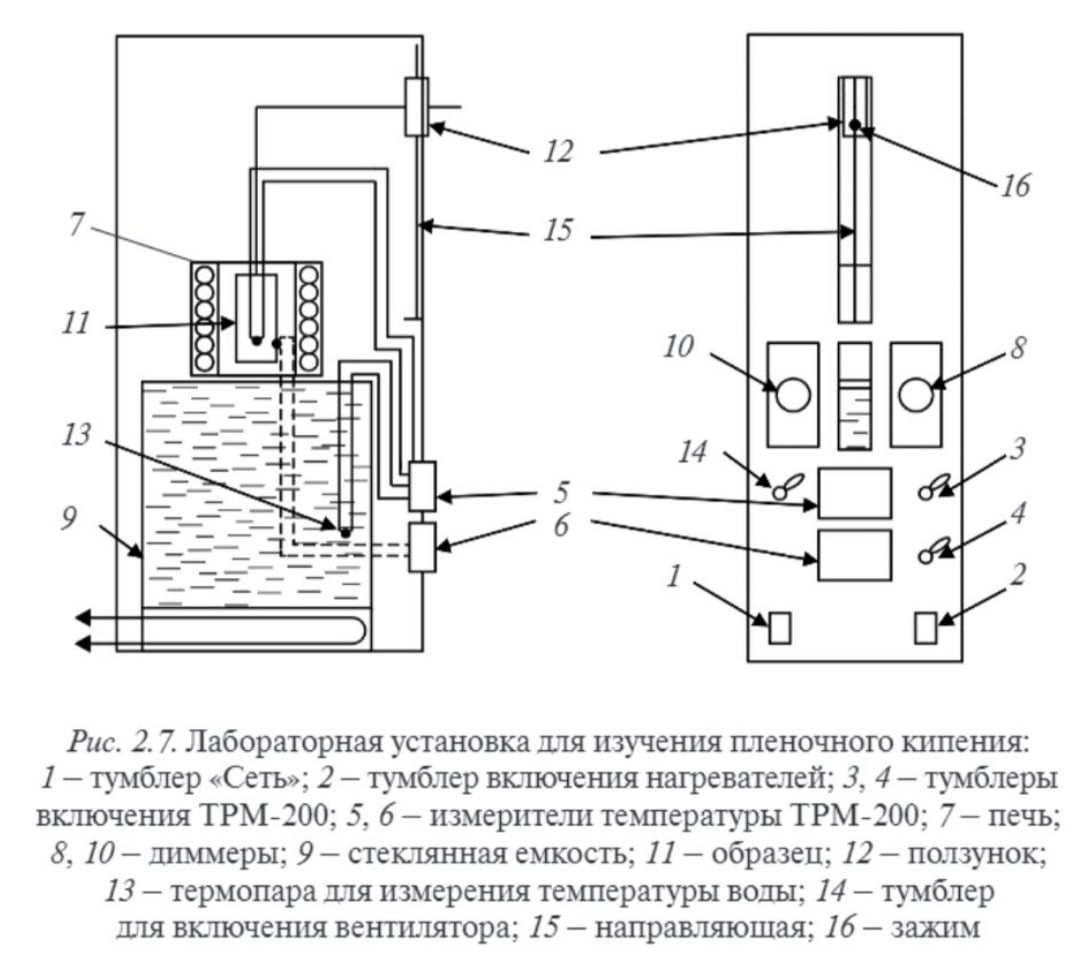
Рисунок 2 – Лабораторная установка для изучения пленочного кипения

1 – тумблер “Сеть”; 2 – тумблер включения нагревателей; 3,4 – тумблеры включения ТРМ-200; 5,6 – измерители температур ТРМ-200; 7 – печь; 8,10 – диммеры; 9 – стеклянная емкость; 11 – образец; 12 – ползунок; 13 – термопара для измерения температуры воды; 14 – тумблер для включения вентилятора; 15 – направляющая; 16 – зажим.

3. Результаты эксперимента

Таблица 1

Результаты измерений

Время τ, с
1	357,7	366,8	99,1
2	357,2	367,4	99,2
3	358,3	367,7	99,1
4	358,8	362,5	99,1
5	359,4	342,5	99,2
6	359,5	322,9	99,2
7	359,4	306,7	99,2
8	359,1	292,7	99,3
9	358,2	280,4	99,3
10	356,9	269,4	99,3
11	355,1	259,7	99,3
12	353	251,3	99,3
13	350,6	244	99,3
14	348	237,5	99,3
15	345,2	231,8	99,3
16	342,4	226,7	99,4
17	339,7	222,1	99,3
18	336,9	218,1	99,4

Продолжение таблицы 1

Результаты измерений

Время τ, с
19	334,2	214,5	99,3
20	331,6	211,2	99,4
21	329,1	208,2	99,4
22	326,6	205,6	99,4
23	324,2	203,1	99,4
24	321,9	200,9	99,4
25	319,6	198,9	99,4
26	317,5	197,1	99,4
27	315,4	195,3	99,4
28	313,3	193,8	99,4
29	311,3	192,4	99,4
30	309,3	191	99,4
31	307,4	189,8	99,4
32	305,6	187,6	99,4
33	303,7	186,5	99,4
34	302	186,5	99,5
35	300,3	185,7	99,5
36	298,6	184,8	99,5
37	297	183,9	99,5
38	295,3	183,1	99,5
39	293,7	182,3	99,5
40	292,2	181,6	99,5
41	290,6	180,9	99,5
42	289,2	180,3	99,5
43	287,7	179,6	99,5
44	286,3	178,4	99,6
45	284,8	178,4	99,6
46	283,5	177,9	99,6
47	282,1	177,3	99,6
48	280,8	176,8	99,5
49	279,5	175,7	99,5
50	276,9	175,2	99,5
51	275,6	174,7	99,5
52	274,4	174,2	99,5
53	273,2	173,3	99,6
54	272	173,3	99,5
55	269,7	172,4	99,6
56	268,6	172,1	99,6
57	267,5	171,7	99,6
58	266,3	171,3	99,6
59	265,3	170,6	99,6
60	263,2	170,3	99,6

4. Обработка результатов

Согласно значениям температуры, полученным при оцифровке видеозаписи, строим график в осях ln( - ) и τ:

Рисунок 3 – график зависимости τ = f ln( - )

По наклону кривой к оси абцисс оцениваем темп охлаждения:

, ,

где значения разности ( - ) в момент времени 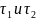соответственно.

Пример расчета:

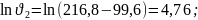
Расчет поверхности теплообмена:

F = , м²,

.

где d – диаметр цилиндра, h – глубина погружения в воду.

Расчет удельной изобарной теплоемкости образца:

+ ,

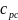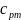где , , – масса оболочки, цилиндра, образца, удельные изобарные теплоемкости стали и меди = 510 , – 390 .

Расчет коэффициента теплоотдачи:

=

Расчет коэффициента теплоотдачи боковой поверхности и дна:

,

где: = 2,37 теплопроводность сухого насыщенного пара,

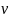=20,02 – кинематическая вязкость сухого насыщенного пара,

r=2256,8 – удельная теплота парообразования,

= 0,598 – плотность сухого насыщенного пара,

= 958,4 – плотность насыщенной жидкости,

характерный размер (для дна =d, для боковой поверхности =h),

c – поправочный коэффициент на расположение поверхности (для горизонтальной поверхности =0,72, для вертикальной поверхности =0,943),

– разница между поверхностью теплообмена и жидкостью.

Пример расчета при 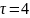c:

,

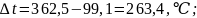
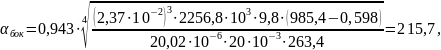
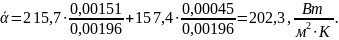
Определим плотность теплового потока:

где - средние по объему значения температур образца в момент времени 𝜏₁ и 𝜏₂ соответственно.

На малых отрезках времени для каждого времени 𝜏 можно воспользоваться линейной аппроксимацией

где 𝑡₁₃, 𝑡₁₄ – температуры вблизи поверхности и в середине образца, .

Пример расчета для с:

Определим предельный перегрев жидкости, учитывая, что давление в лаборатории во время проведения эксперимента 𝑝 = 760 мм рт. ст.

Определим критический температурный напор:

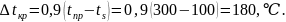
Таблица 2

Результаты вычислений

		q
с
4	202,32	1742,43
5	206,37	1751,41
6	210,75	1464,00
7	214,75	1284,37
8	218,56	1185,57
9	222,18	1104,74
10	225,69	1032,88
11	229,02	943,07
12	232,12	871,22
13	235,00	817,33
14	237,71	763,44
15	240,23	709,55
16	242,65	655,66
17	244,84	610,75
18	246,93	565,84
19	248,78	529,91
20	250,65	493,99
21	252,36	458,06
22	253,89	440,10
23	255,41	404,17
24	256,78	386,21
25	258,06	350,28
26	259,24	350,28
27	260,45	323,34
28	261,48	305,37
29	262,46	305,37
30	263,46	278,43
31	264,33	359,26

Продолжение таблицы 2

Результаты вычислений

		q
с
32	265,96	269,45
33	266,79	152,69
34	266,87	224,54
35	267,49	233,52
36	268,19	224,54
37	268,90	224,54
38	269,54	215,56
39	270,19	197,60
40	270,77	206,58
41	271,35	179,63
42	271,85	197,60
43	272,44	233,52
44	273,56	134,72
45	273,56	161,67
46	273,99	179,63
47	274,52	161,67
48	274,88	215,56
49	275,86	278,43
50	276,32	161,67
51	276,78	152,69
52	277,24	188,61
53	278,17	107,78
54	278,08	287,41
55	279,03	125,74
56	279,32	134,72
57	279,70	143,71
58	280,09	152,69
59	280,78	215,56
60	281,08	-

Определим вторую критическую плотность теплового потока:

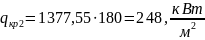
Сопоставим полученный результат со значением, рассчитанным по методике С. С. Кутателадзе:

Можно увидеть, что 𝑞_кр2, найденные по разным формулам отличаются в 10 раз.

Оценим неопределенность вычислений, учитывая, что 𝑢_𝛼кр2 = 10, Вт/м²; 𝑢_Δ𝑡кр = 0,5, К: