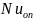САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа ТМО-6

"Определение коэффициента теплоотдачи от горизонтальной трубы при свободно-конвективном теплообмене в воздушной среде"

Студент гр. 3231401/20002 ______Школьников А.С.

Студент гр. 3231401/20002 ______Сирош С.А.

Преподаватель ________________ Павлов А. В.

Содержание

1. Введение 3

2. Описание установки 6

3. Результаты эксперимента 7

5. Вывод 10

1. Введение

Свободно-конвективным называют такой вид теплообмена между твердой поверхностью и омывающей ее жидкостью в котором движение жидкости вызывается самим процессом теплообмена. Примером является обогрев помещения батареями центрального отопления.

При свободной конвекции частицы жидкости, соприкасаясь с твердой поверхностью, меняют свою температуру. Под частицами жидкости мы понимаем не молекулы или атомы. Речь идёт о малых, но макроскопических объёмах жидкости, в которых проявляются такие понятия, как температура, плотность и т.д. При нагреве плотность таких частиц изменяется, и они «всплывают» или «тонут». Их место занимают более холодные или более нагретые частицы, в свою очередь, повторяя описанный процесс. Так возникают конвективные токи жидкости, обусловленные разностью температур стенки и жидкой среды и вызванные разностью плотностей различных слоев жидкости в поле силы тяжести. При свободной конвекции задать среднюю скорость течения жидкости или газа сложно и, следовательно, сложно рассчитать число Рейнольдса Re. Поэтому уравнение подобия при свободной конвекции имеет вид Nu = f (Gr, Pr), где – число Грасгофа (ν – кинематическая вязкость воздуха, g = 9,81 м/с2 – ускорение свободного падения, β – изобарный коэффициент объёмного расширения (для воздуха и других сред, по свойствам близких к идеальным газам, β = 1/Tж, где Tж = tж + 273,16 К – абсолютная температура среды)

В данной работе определяется средний коэффициент теплоотдачи от горизонтальной трубы (имитирующей бесконечно длинную трубу в неограниченном пространстве) в условиях свободно-конвективного теплообмена с воздухом.

Средний коэффициент теплоотдачи α определяется по закону Ньютона

Q = α(t_c − t_ж)F, (1)

согласно которому тепловой поток Q, переданный от поверхности к жидкости, пропорционален площади поверхности F и разности температуры поверхности тела t_c и температуры жидкости t_ж. Коэффициент пропорциональности α называют средним коэффициентом теплоотдачи. Он характеризует количество теплоты, передаваемое в единицу времени через единицу поверхности тела при разности температур между поверхностью и потоком в один градус. Для газов и неметаллических жидкостей уравнение подобия при свободно-конвективном теплообмене имеет вид

Nu = C(Gr · Pr)ⁿ, (2)

где – число Прандтля (ν – кинематическая вязкость, a - температуропроводность среды).

Коэффициенты и n определяют либо из аналитического решения системы дифференциальных уравнений конвективного теплообмена (в совокупности с условиями однозначности), либо опытным путём.

Аналитические решения громоздки, сложны и выполнимы только для простейших случаев. Поэтому чаще всего коэффициенты уравнения (2) определяют на основе эксперимента. Определяющим размером для горизонтальной трубы считается её диаметр, поэтому числа подобия записывают так: число Нуссельта: 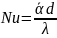( - теплопроводность воздуха), число Грасгофа: , число Прандтля: - температуропроводность воздуха), которое зависит от температуры.

Многочисленными опытами установлено, что в условиях свободно-конвективного теплообмена на горизонтальной трубе уравнение (2) имеет вид

Nu = 0,5(Gr · Pr)^0,25. (3)

Уравнение (3) справедливо при ламинарном движении воздуха вокруг трубы в диапазоне изменения определяющих параметров 10³ ≤ Gr · Pr ≥ 10⁹.

Именно с уравнением (3) следует сопоставить результаты, полученные в настоящих работах.

2. Описание установки

Установка (рисунок 1) представляет собой латунную трубку 2 наружным диаметром 35 мм. В трубку 2 вмонтирован электрический нагреватель 1, расположенный на участке длиной 300 мм (рабочий участок). По электрической мощности, измеренной ваттметром 4, определяют тепловой поток через боковую поверхность рабочего участка.

Для устранения тепловых утечек через торцовые сечения рабочего участка в трубке по обе стороны от него вмонтированы компенсационные нагреватели 3.

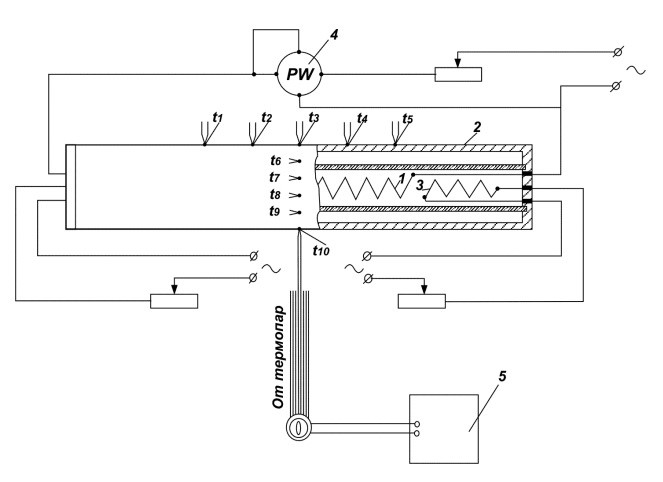
Рисунок 1 – Установка для исследования свободно-конвективного теплообмена

Изменяя ток в компенсационных нагревателях, можно добиться, чтобы температура трубки 2 на рабочем участке была практически одинаковой. Контроль температуры трубки по длине осуществляется термопарами t₁...t₅, зачеканенными на наружной поверхности трубки.

Кроме того, для определения средней температуры наружной поверхности трубки на середине рабочего участка зачеканены по полуокружности термопары t₆...t₁₀. Температура воздуха в помещении t_ж измеряется термометром.

3. Результаты эксперимента

По достижении стационарного процесса последнее измерение температуры принимаем за расчетное, по которому в дальнейшем будем производить вычисления.

Таблица 1

Результаты измерений

Контрольные термопары
t1	t2	t3	t4	t5
∘C
23,9	24,4	24,8	25,3	25,6
43,5	44	44,2	43,9	43,9

Таблица 2

Результаты измерений

W		Рабочие термопары
		t6	t7	t8	t9	t10
Вт	∘C						К		Вт
7	26	44,4	44,4	44,4	44,4	44,4	18,4	1,6
18	26	72,1	71,9	71,8	72	72,1	46	3,8

4. Обработка результатов

Измеренный в опыте тепловой поток передается в окружающую среду не только за счет свободной конвекции, но и за счет теплового излучения:

где Q - конвективная составляющая полного теплового потока Q_Σ;

Q_изл - составляющая, связанная с тепловым излучением с поверхности трубы.

Величину Q_изл определяем для двух режимов по вспомогательному графику (рис.2), при построении которого использован закон Стефана-Больцмана и фактическая степень черноты трубки 2 по средней температуре стенки t_с.

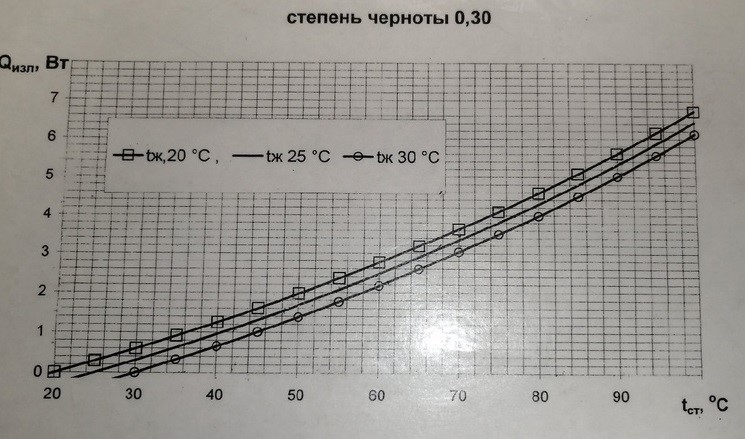
Рисунок 2 – Графики зависимости Q_изл

Конвективную составляющую теплового потока считаем по формуле

(4)

Разность температур (t_c − t_ж) = ΔT определяем как среднеарифмитическую по показаниям t₆...t₁₀:

, (5)

где t_{c i} - температура в i-й точке на поверхности трубы.

Коэффициент теплоотдачи

(6)

где L - длина рабочего участка трубы.

Таблица 3

Результаты расчетов

Q						Pr	Gr	PrGr
Вт	К	Вт/(м2·К)	∘C	м2/с	Вт/(м·К)
5,4	18,4	8,9	26	15,63	2,64	0,73	105893	77302	11,8	8,34
14,7	46	9,7	26	15,63	2,64	0,73	264619	193171	12,9	10,5

Для того, чтобы сравнить результаты опытов с данными, соответствующими формуле (3), представляем опытные данные в виде зависимости Nu = f(Gr · Pr)

Рисунок 3 – Графики зависимости Nu = f(Gr · Pr)

Суммарная стандартная неопределенность измерения коэффициента теплоотдачи состоит из суммы слагаемых неопределенностей величин, входящих в формулу (6), имеет вид:

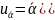
где

Результаты измерений и вычислений:

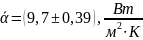
5. Вывод

В ходе проведенной работы был определен тепловой поток, вычислены коэффициенты теплоотдачи для двух тепловых режимов, величина Gr·Pr и число Нуссельта. При анализе результатов, полученных расчетным и экспериментальным путями, можно выявить схожесть этих зависимостей. Угол наклона графиков в логарифмических координатах практически совпадает, но экспериментальный график расположен выше, чем расчетный. Это может быть связано с неопределенностями используемого оборудования, неточностью измерений и подсчетов. Для расчета числа подобия Nu используется формула Nu = C(Gr ·Pr)n, где коэффициенты C и n были подобраны многочисленными опытами при условиях приближенных к идеальным. Поэтому расхождение в графиках может быть вызвано тем, что условия проведения лабораторной работы не были идеальными, а также тем, что стационарный режим, возможно, так и не был достигнут.

Санкт-Петербург

2023