
ТД - 2
.docxСАНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ПЕТРА ВЕЛИКОГО
Институт Энергетики
Высшая школа атомной и тепловой энергетики
Лабораторная работа №ТД - 2
"Определение коэффициента Пуассона для воздуха"
Студент гр. 3231401/20002 ______Школьников А.С.
Студент гр. 3231401/20002 ______Сирош С.А.
Преподаватель ________________ Павлов А. В.
Содержание
1. Введение 3
2. Описание установки 5
3. Результаты эксперимента 6
4. Обработка результатов 7
5. Вывод 7
1. Введение
Адиабатный процесс в идеальном газе описывается уравнением:
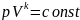
где p — давление газа, Па; V — объем газа,
м3;
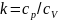 — показатель
— показатель
адиабаты,
или коэффициент Пуассона, равный
отношению изобарной теплоемкости газа
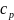 к его изохорной теплоемкости
к его изохорной теплоемкости
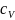 .
.
Если пренебречь зависимостью и от температуры (газ с такими свойствами называют совершенным), то коэффициент Пуассона будет зависеть только от строения молекул газа:
k = 1,66 для одноатомных газов;
k = 1,40 для двухатомных газов;
k = 1,33 для трех- и более атомных газов.
Воздух состоит в основном из двухатомных молекул азота и кислорода, поэтому в первом приближении считают, что для него коэффициент Пуассона равен 1,40. Для более точных расчетов величину к определяют экспериментально.
Опыт выглядит
следующим образом: В баллон через
открытый клапан накачивают воздух,
после чего клапан закрывают. Через
некоторое время температура воздуха
сравнивается с температурой окружающей
среды, а его давление (измеряемое
манометром) становится равным
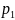 .
.
Далее газ
сжимается от атмосферного давления до
давления
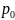 ,
а затем изохорно (при
,
а затем изохорно (при
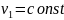 ) охлаждается до начальной температуры
) охлаждается до начальной температуры
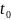 .
.
Затем клапан
кратковременно открывают, давление в
баллоне сравнивается с атмосферным.
Процесс идет достаточно быстро, чтобы
считать его адиабатическим. Температура
воздуха при этом снижается до уровня
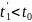 . Клапан вновь закрывают, и в результате
теплообмена через стенку баллона газ
изохорно подогревается до исходной
температуры
.
Давление в баллоне при этом возрастает
до уровня
. Клапан вновь закрывают, и в результате
теплообмена через стенку баллона газ
изохорно подогревается до исходной
температуры
.
Давление в баллоне при этом возрастает
до уровня
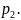
В адиабатном процессе работает формула:
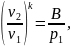
где
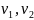 — объем воздуха в баллоне до открытия
клапана и после его закрытия, соответственно.
— объем воздуха в баллоне до открытия
клапана и после его закрытия, соответственно.
Для двух состояний газа на основании закона Бойля—Мариотта:
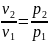
Тогда:
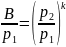
Откуда следует:
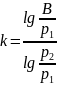
2. Описание установки
Экспериментальная установка представлена на рис. 1. В стеклянный баллон 1, соединенный с компрессором 2, через впускной кран 3 накачивается воздух. Клапан сброса воздуха 4, находящийся на верхней крышке установки, позволяет резко уменьшить давление в баллоне. На передней панели 6 размещаются тумблеры “Сеть” 7, “Компрессор” 8 и водяной U-образный манометр 5. Кран перепуска воздуха 3 имеет положения:
“Открыт” (баллон подключен к выходу компрессора);
“Закрыт” (баллон герметизирован);
“Регулирование уровня” (тонкая регулировка давления после заполнения баллона воздухом).
В ходе работы
в баллон 1 компрессором 2 накачивают
воздух до определенного избыточного
давления (разность уровней в коленах
U-образного манометра
5 должна составлять 200...250 мм вод. ст.). В
каждой серии опытов эта разность должна
быть одинаковой (регулируется краном
3). После охлаждения воздуха в баллоне
до температуры окружающей среды
осуществляют быстрый сброс давления
через выпускное отверстие с клапаном
4. После того как клапан сброса 4 закрылся,
начинается изохорный процесс теплообмена;
температура воздуха в баллоне приближается
к температуре окружающей среды, а
давление поднимается до уровня
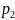 ,
определяемого по манометру 5.
,
определяемого по манометру 5.
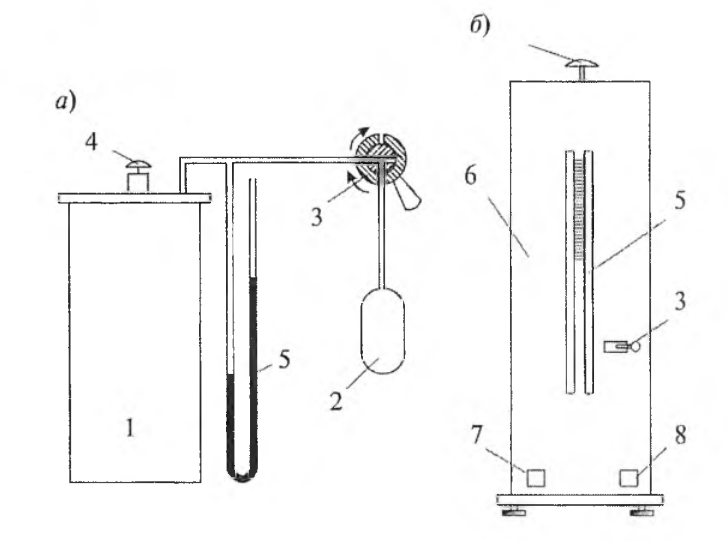
Рисунок 1– Экспериментальная установка: а — схема; б — вид передней панели
1 – стеклянный баллон; 2 – компрессор; 3 – впускной кран; 4 – клапан сброса воздуха; 5 – водяной U-образный манометр; 6 – передняя панель; 7 – тумблер «Сеть»; 8 – тумблер «Компрессор»
3. Результаты эксперимента
Таблица 1
Результаты измерений
Номер опыта |
H1 |
H2 |
H1 – H2 |
h1 |
h2 |
h1 – h2 |
p1 |
p2 |
k |
||
мм вод. ст. |
мм рт. ст. |
|
|||||||||
1 |
275 |
75 |
200 |
185 |
153 |
33 |
761 |
748 |
1,2 |
||
2 |
290 |
40 |
250 |
190 |
145 |
45 |
764 |
749 |
1,2 |
||
3 |
297 |
57 |
240 |
213 |
152 |
61 |
764 |
751 |
1,4 |
||
B = 746 мм рт. ст. |
|||||||||||
4. Обработка результатов
Рассчитаем коэффициент Пуассона:
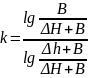
Определим среднее арифметическое значение:
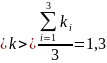
5. Вывод
В данной лабораторной работе был рассчитан коэффициент Пуассона для воздуха, экспериментальное значение k = 1,3. Теоретическое значение kт =1,4 при температуре t ≈ 20 °C. Отличие вероятно связано с тем, что эксперимент подразумевает протекание идеального адиабатического процесса, что в реалии невозможно.
Санкт-Петербург
2023
