САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа №ТМО-1

"Определение теплопроводности воздуха методом нагретой нити"

Студент гр. 3231401/20002 ______Школьников А.С.

Студент гр. 3231401/20002 ______Сирош С.А.

Преподаватель ________________ Павлов А. В.

Содержание

1. Введение 3

2. Описание установки 4

5

3. Результаты эксперимента 7

5. Вывод 10

1. Введение

Основной закон теплопроводности — закон Фурье – утверждает, что плотность теплового потока (теплота, передаваемая в единицу времени через единицу поверхности) пропорциональна градиенту температуры с обратным знаком:

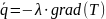
Коэффициент пропорциональности λ характеризует индивидуальную способность сред и материалов проводить теплоту, он численно равен плотности теплового потока при единичном градиенте температуры. Величину λ называют теплопроводностью (ранее использовали термин «коэффициент теплопроводности»), её размерность — Вт/(мК).

В твёрдых телах тепловой поток всегда рассчитывают по уравнению теплопроводности Фурье; передача теплоты в этом случае вызвана движением микрочастиц (электронов, ионов) или особых волн — фононов.

В жидкостях и газах к теплопроводности может добавляться конвективная составляющая теплового потока; однако в малых объёмах и при низких скоростях движения среды ею можно пренебречь.

2. Описание установки

Принципиальная схема экспериментальной установки и вид передней панели модуля, в котором она размещена, представлены на рисунке 1. Нагреваемая вольфрамовая проволока-нить 1 расположена в цилиндрическом стеклянном капилляре 2. Капилляр 2 помещён в стеклянную трубу 3 с внутренним диаметром значительно большего размера, чем диаметр капиллярной трубки. В кольцевом зазоре между капилляром 2 и внешней трубой 3 находится вода. Температуру наружной стенки капилляра t_с полагаем равной температуре воды, циркулирующей в зазоре, и неизменной в течение опыта. Эта температура измеряется хромель-копелевой термопарой 4.

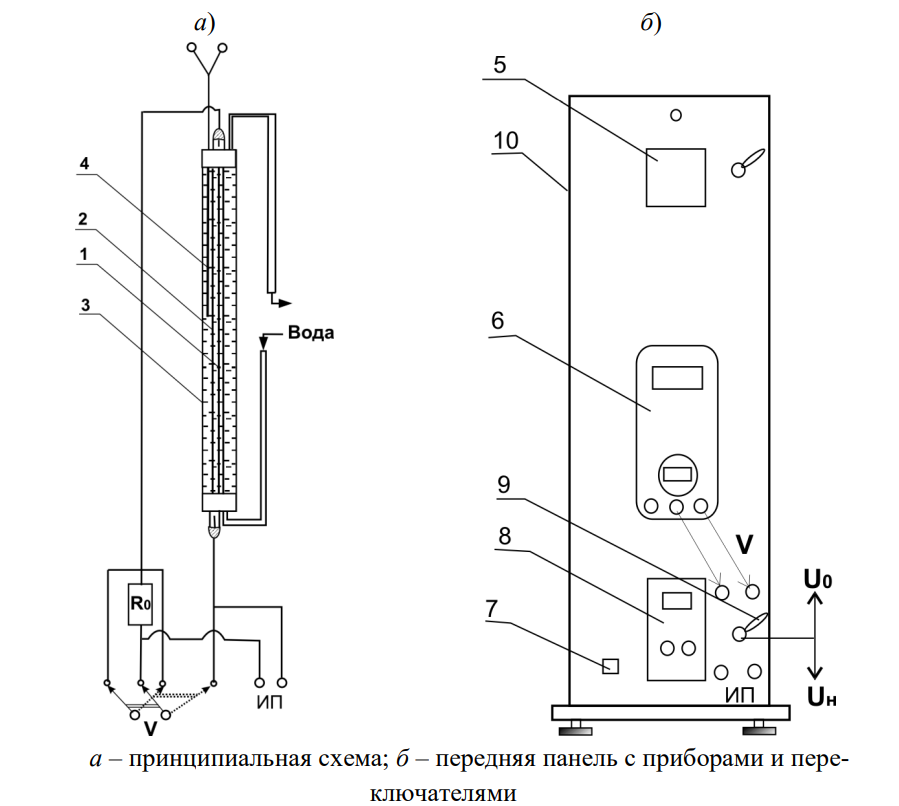
Рисунок 1 - Установка для определения теплопроводности воздуха

Рисунок 2 - Элемент принципиальной схемы длиной ΔL

Баллон с проволокой размещён в модуле 10. Электропитание к проволоке 1 подводится от источника питания 8 через разъёмы. Последовательно с проволокой 1 включено образцовое сопротивление R₀ для определения величины тока в цепи (по падению напряжения на R₀). Для измерения падений напряжения на вольфрамовой проволоке U_R и на образцовом сопротивлении U₀ используется универсальный вольтметр 6 типа МУ-67 с автоматическим переключением пределов измерений.

В верхней части передней панели модуля 10 находится измеритель температуры 5 типа 2ТРМО, к которому подключена хромелькопелевая термопара 4 для измерения температуры воды. В нижней части панели расположены: тумблер электропитания 7, разъёмы для подключения источника питания 8, разъёмы V для подключения вольтметра 6, тумблер 9 для переключения вольтметра на измерение падений напряжения на образцовом сопротивлении (U₀) и напряжения на вольфрамовой проволоке (U_H).

Через 10…15 мин после включения установки температуры проволоки, стенки капилляра, воздуха в нём и охлаждающей воды перестают изменяться – устанавливается стационарный тепловой режим. При этом тепловой поток от проволоки Q_H через слой воздуха и стенку капилляра поступает в воду и далее рассеивается в окружающую среду. Ввиду того, что диаметр вольфрамовой проволоки d₁ значительно меньше d₂ – внутреннего диаметра капилляра, тепловыми потерями через торцы капилляра можно пренебречь. Известно, что плотность теплового потока q, проходящего через цилиндрический слой (в данном случае  слой воздуха), уменьшается обратно пропорционально радиусу. Постоянной на любом радиусе остаётся линейная плотность теплового потока 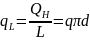. Если термическим сопротивлением стенки капилляра пренебречь, величина будет связана с теплопроводностью и перепадом температуры соотношением:

,

где t_н – температура нагревателя; t_с – температура стенки капилляра.

Среднее значение теплопроводности воздуха в интервале температур t_н … t_с:

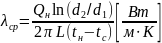
Для использования формулы выше необходимо в опытах замерить или рассчитать следующие величины:

• тепловой поток на поверхности вольфрамовой проволоки Q_н;

• температуру охлаждающей воды t_в, которая в дальнейшем принимается равной температуре стенки (t_в ≈ t_с);

• температуру вольфрамовой нити t_в.

Тепловой поток Q_н = I_нU_н, Вт, находят по измеренному с помощью вольтметра 6 падению напряжения U_н, В, и току I_н = I₀ = U₀/R₀, А.

Температуру вольфрамовой проволоки определяют из соотношения:

где R_он – сопротивление нити при t_н = 22,2 °С;

R_н = U_н/I_н – сопротивление нити при температуре опыта;

 – температурный коэффициент сопротивления материала нити, 1/К

Данные установки и условия опыта:

диаметр вольфрамовой проволоки d₁ = 0,11 мм;

длина нити L = 400 мм;

внутренний диаметр трубки d₂ = 6 мм;

образцовое сопротивление R₀ = 0,1 Ом;

сопротивление нити (при t₀= 22,2 °С) R_он = 3,00 Ом;

температурный коэффициент сопротивления вольфрама

 = 1/К.

3. Результаты эксперимента

Таблица 1.

Результаты измерений.

Номер опыта	tс	Uн	U0	Iн	Qн
	ºC	В	мВ	А	Вт
1	19,5	1,56	0,046	0,46	0,72
2	20,0	2	0,056	0,56	1,12
3	20,6	2,5	0,065	0,65	1,63
4	21,4	3	0,073	0,73	2,19
5	22,3	3,5	0,080	0,80	2,80
6	22,8	4	0,087	0,87	3,48

4. Обработка результатов

Рассчитаем сопротивление нити при температуре опыта

Рассчитаем ток в проволоке

Рассчитаем тепловой поток

Рассчитаем температуру проволоки

Рассчитаем среднюю температуру

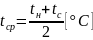
Рассчитаем средние значения теплопроводности воздуха

Рассчитаем неопределенность измерений теплопроводности:

,

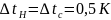где Вт, мм, ,

мм.

Таблица 2.

Результаты расчётов.

№	tн	Rн	λср
	C	Ом	Вт/м·К	C	Вт/м·К
1	53,9	3,4	0,033	36,7	0,023
2	69,8	3,6	0,036	44,9	0,016
3	85,7	3,8	0,040	53,2	0,012
4	109,5	4,1	0,040	65,5	0,009
5	133,3	4,4	0,040	77,8	0,007
6	149,2	4,6	0,044	86,0	0,006

Конечные результаты:

Построим графики зависимости λ_ср (t_ср) и табличные значения λ(t):

Рисунок 3 – График зависимости λ_ср (t_ср)

5. Вывод

Санкт-Петербург

2023