4. Обработка результатов
Расчет
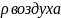 :
:

Расчет скорости набегающего потока идеальной жидкости с учетом коэффициента = 0,92:
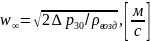
Определим число Рейнольдса
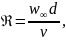
Рассчитаем:
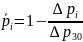
Таблица 2 – Результаты расчетов для 1 режима
θ, град |
l, мм сп. ст. |
|
|
|
0 |
2 |
1,962 |
0,667 |
0,667 |
10 |
2 |
1,962 |
0,667 |
0,657 |
20 |
3 |
2,943 |
0,500 |
0,469 |
30 |
6 |
5,886 |
0 |
0 |
40 |
12 |
11,772 |
-1 |
-0,766 |
50 |
19 |
18,639 |
-2,167 |
-1,393 |
60 |
29 |
28,449 |
-3,833 |
-1,917 |
70 |
38 |
37,278 |
-5.333 |
-1,824 |
80 |
43 |
42,183 |
-6,167 |
-1,071 |
90 |
43 |
42,183 |
-6,167 |
0 |
100 |
41 |
40,221 |
-5,833 |
1,013 |
110 |
40 |
39,240 |
-5,667 |
1,938 |
120 |
40 |
39,240 |
-5,667 |
2,833 |
130 |
40 |
39,240 |
-5,667 |
3,643 |
140 |
40 |
39,240 |
-5,667 |
4,341 |
150 |
42 |
41,202 |
-6 |
5,196 |
Продолжение таблицы 2 – Результаты расчетов для 1 режима
θ, град |
l, мм сп. ст. |
, Па |
|
|
160 |
41 |
40,221 |
-5,833 |
5,482 |
170 |
41 |
40,221 |
-5,833 |
5,745 |
180 |
41 |
40,221 |
-5,833 |
5,833 |
Таблица 3 – Результаты расчетов для 2 режима
θ, град |
l, мм сп. ст. |
, Па |
|
|
0 |
22 |
21,582 |
0,185 |
0,185 |
10 |
20 |
19,62 |
0,259 |
0,255 |
20 |
21 |
20,601 |
0,222 |
0,208 |
30 |
27 |
26,487 |
0 |
0 |
40 |
34 |
33,354 |
-0,259 |
-0,198 |
50 |
43 |
42,183 |
-0,592 |
-0,380 |
60 |
53 |
51,993 |
-0,962 |
-0,481 |
70 |
61 |
59,841 |
-1,259 |
-0,430 |
80 |
66 |
64,746 |
-1,444 |
-0,250 |
90 |
66 |
64,746 |
-1,444 |
0 |
100 |
63 |
61,803 |
-1,333 |
0,231 |
110 |
62 |
60,822 |
-1,296 |
0,443 |
120 |
60 |
58,86 |
-1,222 |
0,611 |
130 |
61 |
59,841 |
-1,259 |
0,809 |
140 |
61 |
59,841 |
-1,259 |
0,964 |
150 |
62 |
60,822 |
-1,296 |
1,122 |
160 |
63 |
61,803 |
-1,333 |
1,252 |
170 |
64 |
62,784 |
-1,370 |
1,349 |
180 |
65 |
63,765 |
-1,407 |
1,407 |
Таблица 4 – Результаты расчетов для 3 режима
θ, град |
l, мм сп. ст. |
, Па |
|
|
0 |
21 |
20,601 |
0,222 |
0,222 |
10 |
19 |
18,639 |
0,296 |
0,291 |
20 |
20 |
19,620 |
0,259 |
0,243 |
30 |
27 |
26,487 |
0 |
0 |
40 |
37 |
36,297 |
-0,370 |
-0,283 |
50 |
48 |
47,088 |
-0,777 |
-0,499 |
60 |
60 |
58,860 |
-1,222 |
-0,611 |
70 |
72 |
70,632 |
-1,666 |
-0,570 |
80 |
78 |
76,518 |
-1,888 |
-0,328 |
Продолжение таблицы 4 – Результаты расчетов для 3 режима
θ, град |
l, мм сп. ст. |
, Па |
|
|
90 |
78 |
76,518 |
-1,888 |
0 |
100 |
75 |
73,575 |
-1,777 |
0,308 |
110 |
74 |
72,594 |
-1,740 |
0,595 |
120 |
74 |
72,594 |
-1,740 |
0,870 |
130 |
75 |
73,575 |
-1,777 |
1,142 |
140 |
76 |
74,556 |
-1,814 |
1,390 |
150 |
77 |
75,537 |
-1,851 |
1,603 |
160 |
78 |
76,518 |
-1,888 |
1,774 |
170 |
79 |
77,499 |
-1,925 |
1,896 |
180 |
80 |
78,480 |
-1,962 |
1,962 |
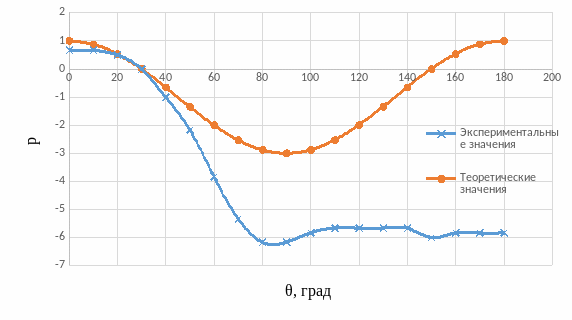
Рисунок 10 – График – θ на первом режиме

Рисунок 11 – График – θ на втором режиме

Рисунок 12 – График – θ на третьем режиме
Рассчитаем коэффициент лобового сопротивления
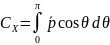
Номер режима |
|
Re |
|
|
1 |
2,92 |
3759 |
7,25 |
1,05 |
2 |
6,19 |
7969 |
1,70 |
1,1 |
3 |
6,19 |
7969 |
2,36 |
1,1 |
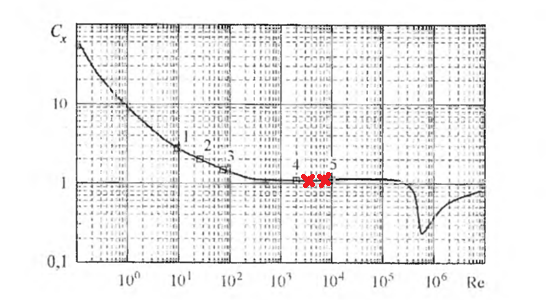
Рисунок 13 – Экспериментальные точки на рисунке 2
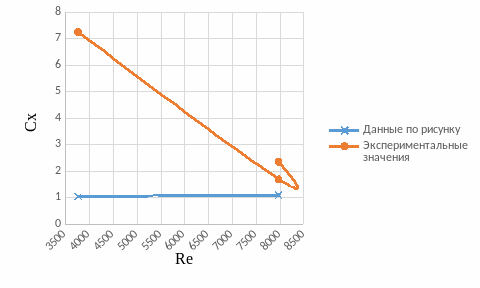
Рисунок
14 – График зависимости
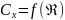
5. Вывод
В ходе лабораторной работы для трех режимов были экспериментально получены зависимости коэффициента давления от азимутального угла 𝑝 = 𝑓(𝜃) для 3 режимов скорости потока, которые отличаются от теоретических. В теории максимальное давление приходится на переднюю и заднюю критические точки. В эксперименте же сохраняется только первое условие, когда максимальный коэффициент давления приходится на переднюю критическую точку. Для задней точки теоретическое распределение давления не выполняется, так как в кормовой части происходит отрыв пограничного слоя воздуха, и в потоке за цилиндром образуется рециркуляционная зона с вихревой структурой течения. Получившиеся результаты зависимости коэффициента лобового сопротивления одиночного цилиндра от числа Рейнольдса 𝐶𝑥 = 𝑓(𝑅𝑒) отличаются от значений, взятых из графика, построенного на основе многочисленных измерений.
Санкт-Петербург
2023

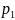 ,
Па
,
Па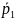

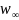 ,
м/с
,
м/с