САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа №МЖГ – 3

"Лобовое сопротивление одиночного цилиндра при поперечном обтекании"

Студент гр. 3231401/20002 ______Школьников А.С.

Студент гр. 3231401/20002 ______Сирош С.А.

Студент гр. 3231401/20002______Манифасова А.Н.

Преподаватель ________________ Коршунов А. В.

Содержание

1. Введение 3

2. Описание установки 10

3. Результаты эксперимента 12

4. Обработка результатов 13

1. Введение

В курсе «Механика жидкости и газа» в разделе «Плоское потенциальное течение несжимаемой жидкости» подробно рассматривается задача о поперечном обтекании круглого цилиндра однородным потоком идеальной несжимаемой жидкости. Получено, в частности, распределение давления по поверхности цилиндра

где – коэффициент давления; – давление на поверхности цилиндра, Па; , Па и , м/с – давление и скорость набегающего на цилиндр однородного потока; ρ – плотность текущей среды, кг/м³ ; θ – азимутальный угол, .

При обтекании цилиндра вязкой жидкостью в передней его части течение безотрывное, и вычисленное по формуле выше распределение давления близко к экспериментальному. В кормовой части цилиндра течение резко отличается от картины, полученной в потенциальной теории. Как следует из формулы коэффициента давления и теоретической кривой – θ, воспроизводящей эту формулу на рисунке 1, максимум давления расположен в передней (А) и задней (В) критических точках, где

где p^* – полное давление в потоке. Начиная от передней критической точки, давление в направлении течения снижается до минимума, соответствующего углам θ, равным 90 и 270°. Поэтому при обтекании вязкой жидкостью причин для отрыва пограничного слоя в передней части цилиндра нет. В кормовой же части цилиндра давление, согласно теоретическому решению, должно резко повышаться, что при обтекании вязкой жидкостью нереально: при значительном положительном градиенте давления пограничный слой срывается с поверхности цилиндра. В потоке за цилиндром образуется рециркуляционная зона со сложной вихревой структурой течения, что резко и отличает реальную картину распределения давления в кормовой части цилиндра от теоретической.

Рисунок 1 – Распределение давления: I – Re  100; II – Re  10⁵

В идеальной жидкости пограничный слой отсутствует, вследствие чего никакого отрыва с поверхности цилиндра произойти не может, и кривая распределения давления по поверхности цилиндра оказывается симметричной относительно вертикальной оси. Это результат проявления парадокса Даламбера, согласно которому при безвихревом обтекании тела конечных размеров идеальной жидкостью проекция суммарной силы давления потока на тело в направлении течения равна нулю.

Реальная картина поперечного обтекания цилиндра при различных числах Рейнольдса подробно изучена экспериментально. Результаты многочисленных опытов представлены на рисунке 2 в виде зависимости коэффициента лобового сопротивления С_х от числа Рейнольдса Re.

Коэффициентом лобового сопротивления называют безразмерную силу P_х, действующую на обтекаемое тело в направлении течения:

Где F_м – площадь миделева сечения.

В диапазоне чисел 0 < Re ⩽ 10 (точка 1 на рисунке 2 и фрагмент течения на рисунке 3) силы вязкости велики по сравнению с силами инерции, поэтому заметного отрыва потока в кормовой части цилиндра не наблюдается.

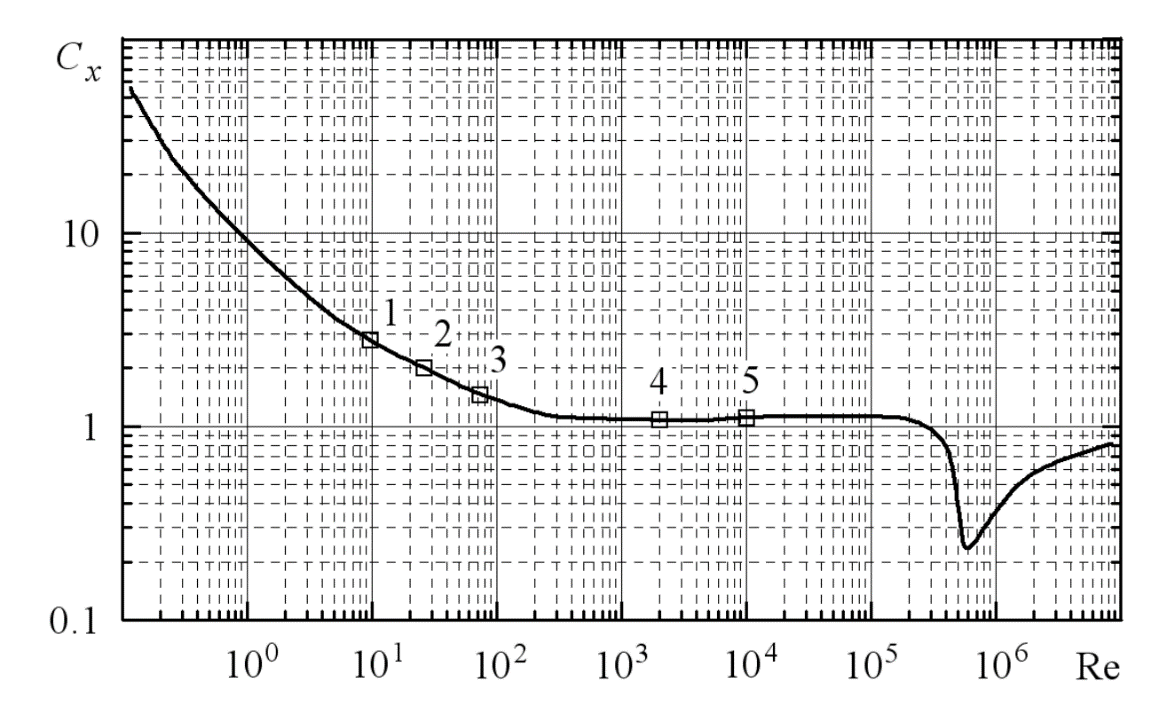
Рисунок 2 – Коэффициент сопротивления цилиндра

Распределение давления по поверхности цилиндра мало отличается от теоретического (симметричного), и проекция суммарной силы давления на направление течения мала. Эту проекцию силы давления называют силой сопротивления давления P_{х давл}. Ее в случае необходимости нетрудно вычислить по измеренному распределению давления на поверхности цилиндра (см. рисунок 2):

Рисунок 3 – Фрагмент течения вблизи цилиндра при Re = 9,6

Однако в вязкой среде на поверхности цилиндра возникают касательные напряж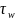ения , в результате чего появляется сила лобового сопротивления

Рисунок 4 – Фрагмент течения вблизи цилиндра при Re = 26

При более высоких числах Рейнольдса (точка 2 на рисунке 2 и фрагмент течения на рисунке 4) непосредственно за цилиндром развивается отрывное течение с явно выраженной почти симметричной и стационарной двухвихревой структурой. В диапазоне чисел Re 30≤ Re ≤40 двухвихревая структура теряет устойчивость, и при числе Рейнольдса Re ≈ 60, за цилиндром формируется движущаяся цепочка периодически образующихся вихрей (точка 3 на рисунке 2 и фрагмент течения на рисунке 5). Эту цепочку вихрей называют вихревой дорожкой Кармана.

Рисунок 5 – Фрагмент течения вблизи цилиндра при Re = 73

На этих режимах распределение давления по поверхности цилиндра становится резко несимметричным относительно вертикальной оси (см. рисунок 1), и силой сопротивления давления P_{х давл} пренебрегать уже нельзя. Силу лобового сопротивления теперь следует вычислять как сумму сил сопротивления трения и сопротивления давления:

Рисунок 6 – Фрагмент течения вблизи цилиндра при Re = 2·10³

Рисунок 7 – Фрагмент течения вблизи цилиндра при Re = 10⁴

При увеличении числа Рейнольдса вихревая дорожка за цилиндром продолжает формироваться, однако периодичность ее структуры нарушается (точка 4 на рисунке 2 и фрагмент течения на рисунке 6), а при числах Re порядка 10⁴ вихревые «комки» в дорожке становятся размытыми вследствие турбулизации течения в следе (точка 5 на рисунке 2 и фрагмент течения на рисунке 7). Заметим, что пограничный слой на передней части поверхности цилиндра при числах Re < 10⁵ вплоть до точки отрыва остается ламинарным.

Дальнейший рост числа Рейнольдса приводит к возникновению кризиса сопротивления. Как показывает опыт, при увеличении числа Re от 10⁵ до 7·10⁵ коэффициент лобового сопротивления снижается более чем в 3 раза (см. рисунок 2). Это связано с тем, что пограничный слой на поверхности цилиндра становится турбулентным. Турбулентные пульсации (в особенности их поперечные составляющие) резко интенсифицируют обмен количеством движения между пограничным слоем и внешним потоком, что препятствует появлению на стенке нулевого напряжения трения, которое предшествует отрыву. В результате угол отрыва потока θ перемещается вниз по потоку приблизительно от 80 до 120 (см. рисунок 1). Значительное сокращение зоны отрывного течения резко снижает сопротивление давления.

Явлением кризиса сопротивления широко пользуются в технике. Если обтекание какого-либо тела происходит с отрывом пограничного слоя, то практически всегда его целесообразно турбулизировать, чтобы резко снизить сопротивление отрыва. С этой целью применяют различные возмущающие течение турбулизаторы: выступы, канавки, повышающую шероховатость насечку на поверхности перед точкой ламинарного отрыва. Если же обтекание происходит безотрывно, то турбулизация пограничного слоя окажется, конечно же, вредной.

Данная работа посвящена экспериментальному определению лобового сопротивления цилиндра в зависимости от числа Рейнольдса. Лабораторная установка обеспечивает изменение числа Рейнольдса Re в диапазоне 10³…10⁴. В этой области сила сопротивления трения P_x составляет примерно 4…5 % от общей силы сопротивления. Поскольку неопределённость измерения давления составляет не менее 5 %, можно считать силу P_x пренебрежимо малой, полагая, что P_x ≈ P_{x давл}