САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа №МЖГ-2

"Местные сопротивления при течении в трубах"

Студент гр. 3231401/20002 ______Школьников А.С.

Студент гр. 3231401/20002 ______Сирош С.А.

Студент гр. 3231401/20002______Манифасова А.Н.

Преподаватель ________________ Коршунов А. В.

Содержание

1. Введение 3

2. Описание установки 5

3. Результаты эксперимента 6

4. Обработка результатов 7

5. Вывод 18

1. Введение

Работа посвящена экспериментальному определению потерь давления в местных сопротивлениях. Эти потери – составная часть общих потерь давления в трубопроводе, которые характеризуют диссипацию механической энергии в канале и входят в виде слагаемого в уравнение Бернулли.

Местные сопротивления возникают при изменении сечения и/или повороте потока, когда структура течения резко меняется. К местным сопротивлениям относятся, например, дроссельные шайбы (в частности, нормальные диафрагмы для измерения расхода), регулировочные устройства (клапаны, задвижки, вентили), внезапные расширения или сужения, повороты канала.

Как правило, для местных сопротивлений принимают, что вызванные ими дополнительные потери давления сосредоточены в одном сечении. В действительности местное сопротивление влияет на структуру потока как вниз, так и вверх по течению. Длина зоны возмущения от местного сопротивления за ним обычно значительно больше, чем перед ним. Для измерения потерь давления на местном сопротивлении отборы давления следует размещать в сечениях, где возмущения от местного сопротивления затухают.

При течении жидкости через местные сопротивления потери давления

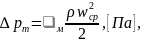
где _м – коэффициент местного сопротивления;  – плотность жидкости, м3/с; w_ср – осредненная по расходу скорость потока, м/с.

Структура формулы выше обоснована теорией гидродинамического подобия, согласно которой при стационарном движении несжимаемой жидкости и в отсутствие влияния силы тяжести для гидродинамически подобных течений число Эйлера Eu = 2p/(w²) однозначно связано с числом Рейнольдса Re = wD/. Поэтому коэффициент местного сопротивления зависит от числа Рейнольдса и от нарушающих гидродинамическое подобие факторов. Во многих местных сопротивлениях главный фактор, нарушающий структуру течения, – конфигурация проточной части, а влияние относительной шероховатости и числа Рейнольдса оказывается пренебрежимо малым. Говорят, что такое течение автомодельно как по числу Рейнольдса, так и по относительной шероховатости. Лишь для вычисления коэффициента сопротивления _м при внезапном расширении существует простая приближенная зависимость (формула Борда). Коэффициенты _м для других местных сопротивлений определяют, как правило, по обобщенным эмпирическим данным, сводка которых приводится в гидравлических справочниках. Данная работа посвящена опытному определению коэффициентов сопротивления _м для некоторых видов местных сопротивлений: дроссельной шайбы (нормальной диафрагмы), задвижки (дроссельного клапана), внезапного расширения, внезапного сужения и поворотов потока. Экспериментальные результаты сравниваются с обобщенными эмпирическими данными.

2. Описание установки

Схема лабораторной установки для исследования потерь давления на местных сопротивлениях показана на рисунке 1

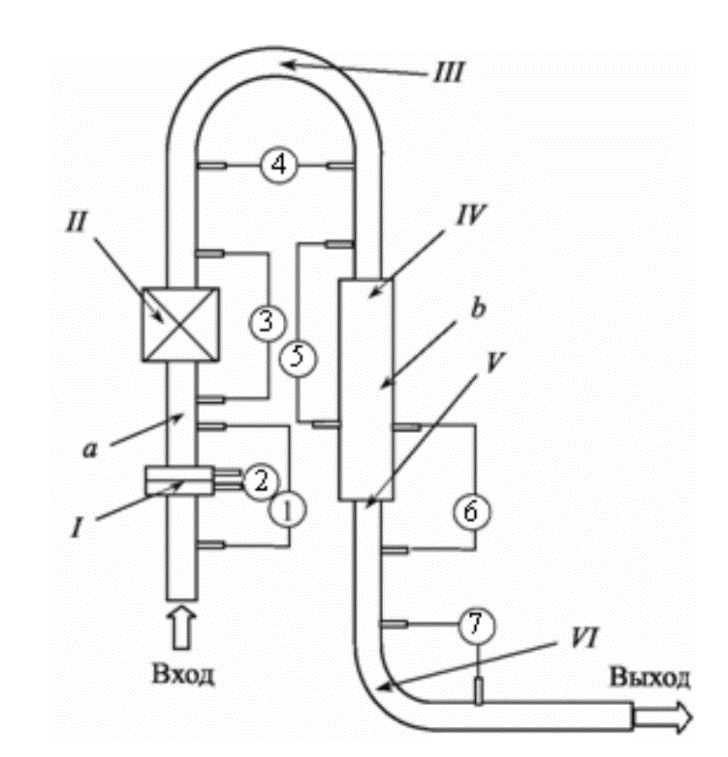
Рисунок 1 – Схема установки для определения потерь давления на местных сопротивлениях

Здесь I – дроссельная шайба (нормальная диафрагма), II – задвижка (дроссельный клапан), III – колено с поворотом потока на 180, IV – внезапное расширение, V – внезапное сужение, VI – колено с поворотом потока на 90, а – труба диаметром 16 мм, b – труба диаметром 26 мм. Перепады давления на участках трубопровода, в которых размещены местные сопротивления, измеряют дифференциальными манометрами 1, 3  7. Перепад давления в камерах нормальной диафрагмы измеряют дифференциальным манометром 2.