27. Сведение дифференциального уравнения к интегральному
Теорема 1. Пусть в уравнении
(4.1)
1)
функция f(x,y)
непрерывна в области
:
;
2) функция f(x,y) удовлетворяет условию Липшица по y:
,
.
Лемма:
Интегрировать лучше чем дифференцировать => интегрируем
(получили
интеграл)
Возьмем
x=
Пусть есть
,
т.е.
уравнение удовлетворяет нач. усл.
Из этого следует что дифф уравнение можно заменить интегральным при наличии начального условия
28. Теорема о существовании и единственности решения дифференциального уравнения 1-го порядка.
Теорема. Пусть в уравнении
(1)
1) функция f(x,y) непрерывна в области : ;
2) функция f(x,y) удовлетворяет условию Липшица по y:
, .
Тогда
существует и притом единственное в
решение y
= y(x)
уравнения (1), такое что
y(x0) = y0 (2)
где
,
.
Доказательство.
Рассмотрим
- совокупность всех функций
y(x),
определенных и непрерывных на
с расстоянием
- метрическое пространство (было доказано).
- полно (примем без доказательства).
Дифференциальное уравнение (1) с начальным условием (2) заменим эквивалентным уравнением
(3)
Справедливо следующее утверждение:
Если
f(x)
интегрируема на [a,
b],
то
непрерывна на [a,
b].
Положим
Оператор
ставит в соответствие всякой функции
y(x),
непрерывной на
и не выходящей из области G,
непрерывную функцию A(y)
,
график которой не выходит из области
G,
так как
,
где
и,
следовательно,
.
Оператор А - сжимающий.
Действительно
Оценим
Имеем
.
Возьмем максимум от обеих частей:
.
Выберем
h
так, чтобы
,
тогда
и
оператор А
- сжимающий.
Так
как 
-
полное метрическое пространство,
существует и притом единственное решение
уравнения
A(y) = y,
т.е. единственное решение задачи Коши (1). (2). (Его можно найти методом итераций).
Теорема доказана.
29. Теорема существования и единственности для линейных систем.
Система линейных дифференциальных уравнений первого порядка имеет вид
(32)
Здесь
неизвестные функции (искомые), а
известные функции, которые мы будем
предполагать непрерывными на отрезке
числовой прямой. Используя векторные
и матричные обозначения, систему (32)
можно переписать так:
(33)
где
столбец из неизвестных функций, а
из известных. Требуется найти решение
системы, удовлетворяющее начальному
условию
Заметим,
что система (33) является частным случаем
более общей системы
рассмотренной в предыдущем параграфе.
А именно, у линейной системы правая
часть представляет собой линейную
функцию от
Вектор-функция
определена для
и любых
следовательно,
область
для линейной системы представляет собой
часть пространства
ограниченную двумя плоскостями
и
(см.рис.5).
Д
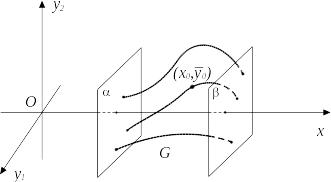
Рис. 5
алее будет доказано, что, в отличие от произвольных систем дифференциальных уравнений, для линейных систем можно гарантировать существование решения на всём отрезке
а не только на маленьком промежутке
Геометрически это означает, что через
каждую точку
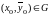проходит интегральная кривая, которая
одним концом “упирается” в плоскость
а другим – в плоскость
(т.е. интегральные кривые “не уходят в
бесконечность”). Сформулируем и докажем
это утверждение.
Теорема
(существования
и единственности решения линейной
системы).
Пусть
дана линейная система
где
матрица и столбец, состоящие из непрерывных
на
функций. Тогда для каждого
и любого вектора
существует решение системы, определённое
на всём отрезке
и это решение единственно.
Доказательство.
Единственность
следует из теоремы для произвольных
систем, поэтому надо доказать лишь
существование решения на всём отрезке
Для этого будем использовать метод
последовательных приближений. Построим
последовательность вектор-функций
Так
как компоненты матрицы
являются непрерывными функциями на
отрезке
то они ограничены. Поэтому существует
константа
такая, что
для всех
и любого вектора
Оценим разности двух соседних членов
последовательности
Для этого положим
Теперь получаем:
и
т.д., т.е.
Отсюда
следует, что для любых
Положим
Тогда
Очевидно,
при
поэтому последовательность
фундаментальна, а значит, равномерно
сходится на отрезке
Предельная функция этой последовательности,
очевидно, является решением дифференциального
уравнения.
Наконец, сформулируем теорему существования и единственности решения линейного уравнения п-го порядка, которая является непосредственным следствием только что доказанной теоремы.
Теорема (существования и единственности решения линейного дифференциального уравнения). Пусть дано линейное дифференциальное уравнение
(34)
где
и
непрерывные на отрезке
функции. Тогда для каждого числа
и любой точки
существует решение
уравнения (34),
определённое на отрезке
и удовлетворяющее начальным условиям
