21. Метрические пространства. Примеры. Дискретное пространство.
22. Пространства в Rn и С[a,b]
23. Предел последовательности точек метрического пространства.
24. Полные метрические пространства. Полнота пространства Rn.
25. Полнота пространства в С[a,b]
26. Принцип сжатых отображений.
27. Сведение дифференциального уравнения к интегральному.
28. Теорема существования и единственности решения диф ур-я 1 порядка
29. Теорема существования и единственности для линейных систем.
30. Формулы Эйлера. Комплексные функции действительного аргумента.
31. Равенство (fg)’=f’g+fg’ для комплексной функции.
32. Производная функции f(x)=eλx (λ из С)
33. Существование ФСР однородного ур-я и системы.
34. Дифференцирование векторов и матриц. Диф. определителя
35. Определитель Вронского и его свойства.
36. Метод вариации для линейных уравнений.
37. Метод вариации для линейных систем.
38. Линейная однородная система с постоянными коэф. Характеристическое уравнение. Решение в случае существования базиса собственных векторов.
39. ФСР однородного ур-я с постоянными коэф. Случай простых действительных и комплексных корней.
40. ФСР однородного ур-я с постоянными коэф в случае кратных корней.
41. Линейные ур-я с постоянными коэф со специальной правой частью: вид частного решения.
42. Уравнение Эйлера
21. Метрические пространства. Примеры. Дискретное пространство.
Метрическим
пространством называется
пара
состоящая из множества
и заданного на этом множестве расстояния
(метрики)
,
т.е. действительной, неотрицательной
функции двух элементов множества,
удовлетворяющей аксиомам
расстояния:
1.
2.
(аксиома симметрии);
3.
(аксиома треугольника).
Примеры:
1.
На любом непустом множестве Х можно
определить метрику следующим образом:
=
.
Такое пространство называется
пространством изолированных точек
(дискретным пространством)
2.
Пусть Х - множество действительных
чисел. В качестве расстояния между
точками возьмем функцию
=
.
Полученное метрическое пространство
называется одномерным арифметическим
пространством или числовой прямой.
Докажем,
что
-
метрика (удовлетворяет трем аксиомам):
из
определения
Симметричность очевидна из определения. Неравенство треугольника – следствие неравенства Шварца.
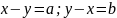
Скалярное
произведение
Следствие из неравенства Шварца
3.
Пусть Х - множество упорядоченных наборов
n вещественных чисел. Тогда для любых
двух его точек
определим расстояние
Получим метрическое пространство,
называемое n-мерным арифметическим
пространством, которое обозначается
4.
– манхэттенская метрика (расстояние
между двумя точками – сумма модулей
разностей координат)
Докажем выполнение аксиом:
Очевидна симметричность. Докажем неравенство треугольника:
известно
?
5. Множество оставим прежним, а метрику определим иначе
Полученное
пространство обозначают
.
6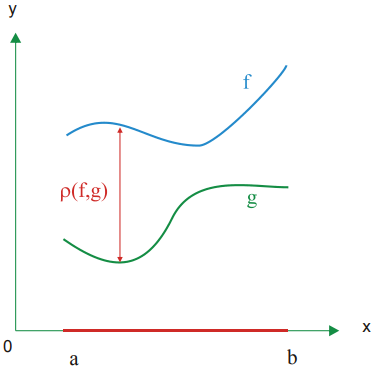
.
Воспользуемся множеством вех функций,
непрерывных на отрезке [a;b]. Расстоянием
между двумя его элементами будем
вычислять по формуле
.
Получили пространство непрерывных на
[a;b] функций (обозначается
)
1-ая
теорема Вейерштрасса: Непрерывная на
отрезке функция ограничена =>
2-ая теорема Вейерштрасса: Непрерывная на отрезке функция имеет наибольшее и наименьшее значение на нем (достигается sup, inf) (неверно для разрывных)
Докажем,
что
– метрика:
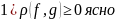
2)
3) Неравенство треугольника:
Неверно:
Верно:
;
7.
– метрика
–
метрика
8.
Возьмем множество числовых
последовательностей, квадраты членов
которых образуют сходящийся числовой
ряд. Метрику определим аналогично
метрике примера 3, т.е.
;
Получили
метрическое пространство, называемое
координатным пространством Гильберта.
22. Пространство и c [a, b]
|
= { (
|
}
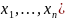n-мерное пространство над полем действ. чисел.
-
обычная евклидова метрика
.
Определение.
Множество Х
называется метрическим
пространством,
если любым двум элементам
поставлено в соответствие действительное
число
(называемое расстоянием
между
и
)
такое, что выполняются аксиомы:
(М1)
причём
(М2)
(симметричность);
(М3)
(неравенство
треугольника).
Докажем
неравенство треугольника для
– известно
x
= (
y
= (
Множество
всех функций, определённых на отрезке
и непрерывных на этом отрезке, является
метрическим пространством относительно
равномерной
метрики
(2)
Докажем
это. Неравенство
очевидно. Также ясно, что
и
Неочевидно лишь неравенство треугольника.
Пусть
Положим
Тогда
и
при всех
Следовательно, для всех
из этого промежутка мы имеем:
Поэтому
т.е.
. Получили пространство непрерывных на [a;b] функций (обозначается )
1-ая теорема Вейерштрасса: Непрерывная на отрезке функция ограничена =>
2-ая теорема Вейерштрасса: Непрерывная на отрезке функция имеет наибольшее и наименьшее значение на нем (достигается sup, inf) (неверно для разрывных)
Докажем, что – метрика:
2)
3) Неравенство треугольника:
Неверно:
Верно: ;
5)
Множество
всех функций
для которых существует
а расстояние, в котором определяется
по формуле
(3)
метрическим
пространством не является, так как в
нём не выполнена аксиома (М1): действительно,
если
при всех
а
функция, равная 0 при
и 1 при
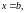то
а
Эту ситуацию можно исправить, отождествляя
такие функции
для которых
т.е. считая такие функции одним элементом
пространства
Тогда
будет метрическим пространством.
Расстояние, определяемое по формуле
(3), называется интегральной
метрикой.
Множество
всех функций
для которых существует
является метрическим пространством
относительно метрики
(4)
если
считать функции
и
для которых
одним и тем же элементом пространства
