16. Линейное уравнение 1 порядка

Дифф-ое уравнение вида y’ + a(x) * y = f(x), где а(х) и f(x) –непрерывные функции х, называется линейным неоднородным дифф-ым уравнением первого порядка

Рассмотрим 2 метода решения:

1)Использование интегрирующего множителя

2)Метод вариации постоянной

Использование интегрирующего множителя

Если линейное дифф-ое уравнение записано в стандартной форме:

y’ + a(x) * y = f(x), то интегрирующий множитель определяется формулой:

Умножение левой части уравнения на интегрирующий множитель u(x) преобразует его в производную произведения y(x) и u(x).

Общее решение диф уравнения выражается в виде:

Метод вариации постоянной

Сначала необходимо найти общее решение однородного уравнения:

y’ + a(x) * y = 0

Общее решение однородного уравнения содержит постоянную интегрирования С. Далее мы заменяем константу С на (пока еще неизвестную) функцию С(х). Подставляя это решение в неоднородное диф. уравнение можно определить функцию С(х)

17. Уравнение Бернулли

y′ + P(x)y = Q(x) ;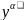

α є ℝ

Делим на :

+P(x) =Q(x)

Eсли α > 0, то теряется решение y = 0.

=z; z′=(1-α)

=

+P(x)z=Q(x)

Решаем, как линейное

z(x)=...

y(x)=...

(см. 16 в-с)

18. Уравнения в полных дифференциалах. Интегрирующий множитель.

Определение уравнения в полных дифференциалах

Дифференциальное уравнение вида

P(x,y)dx+Q(x,y)dy=0 (1)

называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение: du(x,y)=P(x,y)dx+Q(x,y)dy.

Общее решение ур-я в полных дифференциалах определяетсяформулой

u(x,y)=C, где C − произвольная постоянная.

Необходимое и достаточное условие

Пусть функции P(x,y) и Q(x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:

=

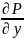
Общий интеграл уравнения (1) имеет вид u(x,y)=C

 или

Алгоритм решения уравнения в полных дифференциалах

1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:

=

2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):

3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:

u(x,y)= +φ(y).

4. Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:

= +φ(y)]= Q(x,y).

Отсюда получаем выражение для производной неизвестной функции φ(y):

φ′ (y)=Q(x,y)− ]

5. Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):u(x,y)=∫P(x,y)dx+φ(y).

6. Общее решение уравнения в полных дифференциалах записывается в виде:

u(x,y)=C.

Интегрирующий множитель

Дано ур-е Mdx+Ndy=0 , которое не является ур-ем в полных дифференциалах, т.е.

Метод введения параметра F(x,y,y’)= 0. Если ур-ие имеет вид: y=f(x,y’),x=f(y,y’)

y=f(x,y’)

y’=p;dy=pdx; y= f(x,y’): dy= df(x,y’)

dy=

pdx= -доказываем ,что оно решается

x= φ(P,c)-решение

Ответ: Ответ в параметрическом виде

x=f(y,y’);y’=p; dx= ;x=

dx=df(y,p)= = – допустим решается

Ответ: