1. Числовой ряд. Критерий Коши сходимости ряда.

2. Бесконечно убывающая геометрическая прогрессия.

3.Признак сравнения с неотрицательными членами

4. Признак Даламбера для рядов с положительными членами

5. Признак Коши (радикальный) для рядов с неотриц. Членами

6. Интегральный признак Коши

7. Условия сходимости ряда Дирихле

8. Абсолютная и условная сходимость ряда.

9. Возможность применения признаков Даламбера и Коши знакопеременными рядами и рядами с комплексными числами

10. Преобразование Абеля. Признаки Абеля-Дирихле.

11. Перестановка членов абсолютно сходящегося ряда

12. Теорема Римана об условно сходящихся рядах

13. Дифференциальное уравнение и система дифференциальных уравнений. Постановки задач. Задача Коши. Сведение уравнения к системе.

14. Уравнение с разделяющимися переменными

15. Однородные уравнения первого порядка

16. Линейное уравнение 1 порядка

17. Уравнение Бернулли

18. Уравнения в полных дифференциалах. Интегрирующий множитель.

19. Метод введения параметра для уравнений, не разрешённых относительно производной.

20. Понижение порядка дифференциального уравнения

1. Числовой ряд. Критерий Коши сходимости ряда.

Ряд – сумма бесконечного числа слагаемых.

Необходимый и достаточный признак сходимости ряда.

Теорема: Ряд сходится <=> последовательность его частичных сумм сходится.

{ } сходится <=> ∀ ε > 0 ∃ N: ∀ n, m ≥ N .

Необходимый признак сходимости:

Если сходится, то .

Д-во: берем .

∀ ε > 0 ∃ N: ∀ n ≥ N .

2. Бесконечно убывающая геометрическая прогрессия.

где

2. Признак сравнения с неотрицательными членами

Теорема (Признак сравнения 1)

Пусть даны два ряда

 a₁ a₂ ...  a_n  ... , n a_n  0 ,

 b₁b₂ ...  b_n  ... , n b_n  0 ,

И n a_n  b_n

Тогда если сходится ряд b_n , то сходится и ряд a_n .

Доказательство

Ряд bn сходится, значит ε  0 n  n (ε) n1, n2 n

<ε

 <ε

Значит : <ε

Замечание 1:

a₁ a₂ ... изменение нескольких членов не влияет на сходимость/ расходимость ряда

Замечание 2:

Аналогично можно доказать расходимость для a_n  b_n

(Если расходится ряд b_n , то расходится и ряд a_n.)

Теорема (Признак сравнения 2)

_a_{n }b_n a_{n ,}b_n >0

_{Если an}(b_n)=0 при n-->   _b_n сходится ,то сходятся и _a_n

_{αn=0 (βn)} при n-->  если |_αn|  c |_βn| c=const

Доказательство

<ε

 c* < c*ε

Следствие

_a_{n }b_n a_{n ,}b_n >0 и a_{n ~} b_n >0 при n--> 

то они сходятся(расходятся) одновременно

4. Признак Даламбера для рядов с положительными членами

_a_n ; a_n > 0

Пусть Ǝ = q

Тогда: при q < 1 - ряд сх-ся

q > 1 – ряд расх-ся

q = 1 - ?

Д-во:

а) q < 1 ; б) q > 1

Возьмём q < < 1 Возьмём q > > 1

q 1 1 q

<

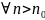
< при k

< = +

Значит, _{- расх.}

<

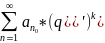_{– сх.,}

Значит, _{ - сх.}

беск. убыв. геом. прогр.

5. Признак Коши (радикальный) для рядов с неотриц. Членами

Пусть Тогда при q : < 1 ряд сходится;

> 1 ряд расходится;

= 1 признак не даёт ответа

Д-во :

1) Пусть q < 1 =>

Аналогично для расход-ти