21. Циркуляция векторного поля. Формула Грина.

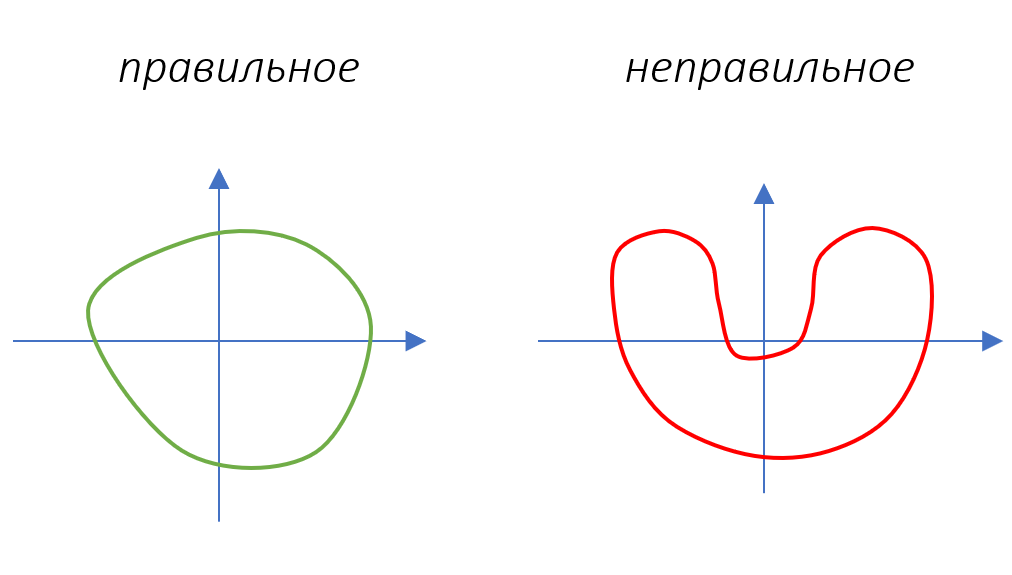
Правильное множество

Будем называть мн-во правильным относительно xy, если любая прямая, параллельная оси, пересекает границу множества в двух точках.

Формула Грина для правильного множества

Пусть есть правильное множество D⊂ℝ² с границей Г (гамма), причём Г ориентирована таким образом, что область остаётся слева.

П усть на всём Dсуществует замкнутое поле а̄ = (P, Q), причём оно такое, что и – непрерывны.

Тогда циркуляция по Г вектора а̄:

∮а̄dr̄ = ∮ Pdx + Qdy = ∬(по D) dxdy

Док-во:

Пойдём справа налево.

Рассмотрим интеграл:

∬(по D) dxdy ⊜

D можно записать так:

Т огда

⊜ = =

На L₂ и L₄ не изменяется =>dx = 0

∮(по Г)Pdx= ∫(по L₁)P(x, y) dx + ∫(по L₃)P(x, y) dx

где

L1: {	x = x	L3: {	x = x
	y = φ(x)		y = ψ(x)

22. Площадь поверхности. Определение. Вычисление площади поверхности, заданной в явном виде и заданной параметрически.

О п р е д е л е н и е. Пусть на поверхности S дана некоторая область ω, разобьём эту область произвольным образом на бесконечно малые ячейки . Тогда площадь поверхности равна сумме площадей всех ячеек .

.

Выберем произвольную точку внутри каждой ячейки, проведём касательную плоскость к поверхности в этой точке и спроектируем ячейку на эту касательную плоскость. Площадь проекции ячейки на касательной плоскости обозначим .. Тогда для площади поверхности имеем

Площадью поверхности называют предел

В ы ч и с л е н и е.

Пусть поверхность S определяется уравнением . Поверхность S предполагается гладкой в каждой точке этой поверхности, то есть существует нормаль к поверхности в каждой её точке. Пусть D есть область определения функции на координатной плоскости Оху. Площадь поверхности над областью D вычисляется по формуле

Доказательство

Угол между этой нормалью и осью Oz определяется соотношением

Спроектируем каждую ячейку на координатную плоскость XOY , в этом случае,

где угол вычислен в точке . В этом случае

Площадь поверхности в параметрическом виде

Пусть поверхность задана в параметрическом виде

Доказательство

Будем считать, что в уравнении поверхности F (x,y,z)=0 параметры x,y,z зависящими от других параметров . Используя правила вычисления производной сложной функции многих переменных, получим

Эти соотношения представляют собой условие перпендикулярности вектора (A, B, C) векторов

Если это так, то вектор с координатами (A, B, C) коллинеарен вектору . Используя условие коллинеарности (пропорциональность одноименных координат), будем иметь

В этом случае интеграл вычисления площади примет вид

при этом следует иметь ввиду, что . .Если ввести обозначения

то площадь поверхности можно вычислить по формуле

.