9. Модуль непрерывности функции многих переменных. Равномерно непрерывные функции. Кратный интеграл от непрерывной функции. Равномерная непрерывность функции. Модуль непрерывности.
Определение
1:
– функция, определенная на множестве
A,
и
при выполнении условия
,
называется равномерно непрерывной.
-
равномерно непрерывная функция на
множестве A,
если выполняется условие
при
.
Теорема 1:
Если
функция непрерывна на D
– измеримом, замкнутом и ограниченном
множестве, то f
– интегрируема на
Доказательство:
Если f – непрерывна на d – замкнутом и ограниченном множестве, то она равномерно непрерывна на d: , ) , . Так как f – непрерывна на d, то она ограничена;
т.к.
f
непрерывна на D,
то она непрерывна и ограничена на
,
)
;
0
Теорема 2 Функция непрерывная на d – измеримом замкнутом ограниченном множестве, равномерно непрерывна на нем
Доказательство:
Допустим что теорема неверна. Равномерно непрерывна:
.
Неравномерно непрерывна
,
тогда
)
значит
ограничено).
- сходящееся(
,
– сходящееся(
значит
Противоречие.
Кратный интеграл от непрерывной функции
Предположим
есть
где
интегрируема
на
Тогда
рассмотрим I(
=
, а потом
10. Свойства кратных интегралов.
Теорема 1. Аддитивное свойство.
Если
f-
интегрируема на
-
измеримом и
- измеримые множества, которые пересекаются
быть может только по границе, то f-
интегрируема на
и
и
+
.
И наоборот. (Доказательство в первом семестре).
Следствие. Пусть f- интегрируема на , если
,
|
|=0,
ограничена
на
,
то
интегрируема
на
и
Доказательство.
Следствие доказано.
Таким образом, понятие интеграла можно распространить на функции, определенные не на всем множестве, но везде, за исключением множества меры 0.
Теорема 2. Однородные свойства.
Если f и g интегрируемы на , то
1)
-
интегрируема
2) k*f- интегрируема.
3) f*g- интегрируема
4)
Если
, то
-
интегрируема.
При этом выполняются равенства:
Теорема 3. Неравенства и теорема о среднем.
Пусть
f
и
g
интегрируемы
на
- измеримом и 𝜑
- интегрируема на
,
,
f≤g
,
тогда по теореме 2
Если
f
ограничена
на
,
то есть A≤f≤B,
то
Доказательство самостоятельно или пока я не соберусь…
Следствие:
- связное измеримое замкнутое, ограниченное
множество, f-
непрерывна на
,
следовательно интегрируема, тогда
Доказательство.
В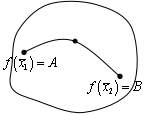
предыдущей теореме возьмем в качестве
,
тогда
.
Надо теперь доказать, что это C
достигается.
Можем рассмотреть функцию одной переменной F(t)
,
,
а так как функция F
у
нас непрерывная (множество связное), то
она принимает все промежуточные значения
между t1и
t2,
значит
.
.
Доказано.
11. Вычисление кратного интеграла для прямоугольной области. Вычисление кратного интеграла в общем случае. Применение общей теоремы для вычисления двойного и тройного интегралов.
Рассмотрим прямоугольную область
f
– интегрируема на
Предположим,
что
интегрируема по
по
теореме о среднем
Помещаем
область D
в прямоугольник
Тогда
