подгон 2018 (легендарный) / 1 курс-20241122T213915Z-001 / _4.1_ Комп Матан / 1 семестр / 3 / V_03_s1

Упражнение С1:

(Стоит формат format short e)!

1) z1 = (1+2*i)^2*(1-i)%. Получим z1 = 1.0000 + 7.0000i; 2) z2 = (1-i)^4-(1+i)^4%. Получим z2 = 0; 3) k = 20:1:40; %(Введем массив) zk = i.^k %(поэлементное возведение)

Получим:

zk =

Columns 1 through 2

1.0000e+000 0 +1.0000e+000i

Columns 3 through 4

-1.0000e+000 0 -1.0000e+000i

Columns 5 through 6

1.0000e+000 0 +1.0000e+000i

Columns 7 through 8

-1.0000e+000 0 -1.0000e+000i

Columns 9 through 10

1.0000e+000 0 +1.0000e+000i

Columns 11 through 12

-1.0000e+000 0 -1.0000e+000i

Columns 13 through 14

1.0000e+000 0 +1.0000e+000i

Columns 15 through 16

-1.0000e+000 0 -1.0000e+000i

Columns 17 through 18

1.0000e+000 0 +1.0000e+000i

Columns 19 through 20

-1.0000e+000 0 -1.0000e+000i

Column 21

1.0000e+000

z4 = (2+5*i)/(1-3*i)+1/(1-i) %Получим: z4 = -8.0000e-001 +1.6000e+000i format rational z4 %= 4/5 + 8/5i format short z4% = -0.8000 + 1.6000i format long z4 %= -0.800000000000000 + 1.600000000000000i format long e z4 %= -7.999999999999998e-001 +1.600000000000000e+000i format short e z4 %= -8.0000e-001 +1.6000e+000i

Упражнение С2:

(Стоит формат format short e)! z1 = sqrt(3)-i; z2 = 1+i*sqrt(3); 1) zc21 = z1*conj(z2)

Получим: zc21 =

0 -4.0000e+000i 2) format short

zc21 = (conj (z1)/z2)^2 Получим: zc21 =

0.5000 - 0.8660i

Упражнение С3:

zc31 = (5+4*i)*(3-2*i^3); %(zc31 = 7.0000 +22.0000i) conj(zc31) = %7.0000 -22.0000i (Сопряженное число) real(zc31) %= 7 (Действительная часть) imag (zc31) %= 22 (Мнимая часть) abs(zc31) %= 23.0868 (модуль комплексного числа) angle(zc31) %= 1.2627 (Аргумент комплексного числа в радианах) syms pi; (angle(zc31)*180)/pi %(Хотел вывести в формате πn. Не получилось) clear pi; pi format short (angle(zc31)*180)/pi %= 72.3499 (Аргумент в градусах)

2. zc32 = (1-i)^13; %= -64.0000 +64.0000i conj(zc32) %= -64.0000 -64.0000i (сопряженное число) real(zc32) %= -64 (действительная часть) imag(zc32) %= 64 (мнимая часть) abs(zc32) %= 90.5097 (модуль числа) angle (zc32) %= 2.3562 (аргумент числа в радианах) (angle(zc32)*180)/pi %= 135 (в градусах)

Упражнение С4: z =(-1 - sqrt(3)*1i)^(1/6); %(Комплексное число)

r = abs(z); %(r – модуль комплексного числа (радиус))

phi = angle(z); %(Аргумент к.ч. в радианах)

n = 0:1:5;

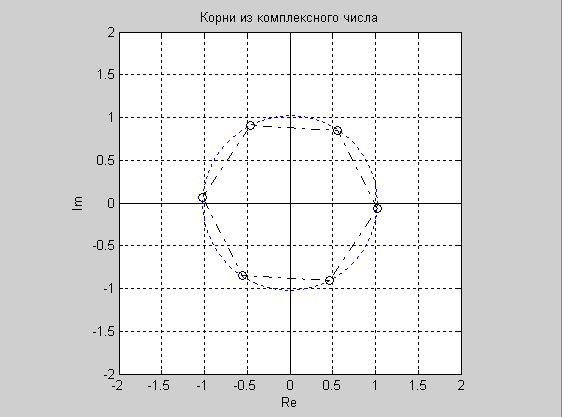
zroot = r^(1/6)*(cos((phi + 2*pi*n)/6)+1i*sin((phi + 2*pi*n)/6)); %(Находим расположение точек на комплексной плоскости)

plot(real(zroot),imag(zroot),'ok-.') %(по заданным точкам строим многоугольник)

hold on %(наносим окружность, на к-й располагаются точки)

t = 0:pi/1000:2*pi; %(По параметрическому уравнению окружности)

x = r^(1/6)*cos(t);

y = r^(1/6)*sin(t);

plot(x,y,'b:')

grid on

xlabel('Re')

ylabel('Im')

title ('Корни из комплексного числа')

axis equal

line([-2 2],[0 0],'Color','black')

line([0 0],[-2 2],'Color','black')

axis([-2 2 -2 2]); %(Выровняли)

Получили:

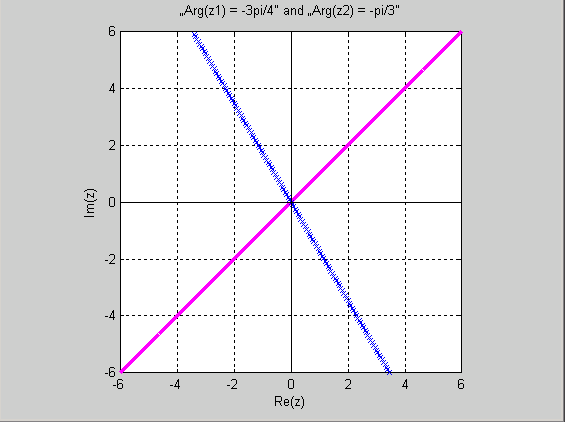
Упражнение С5:

figure (2)

phi1 = -3 * pi / 4;

r = -20:0.1:20;

z1 = r * (cos(phi1) + 1i * sin(phi1)); %(Тригонометрическая форма по аргументу)

phi2 = -pi / 3;

z2 = r * (cos(phi2) + 1i * sin(phi2));

plot(z1, '.m');

hold on

plot(z2, 'xb');

grid on

axis equal

axis([-6 6 -6 6])

line ([-6 6],[0 0],'Color','black')

line ([0 0],[-6 6],'Color','black')

title('_"Arg(z1) = -3pi/4" and _"Arg(z2) = -pi/3"')

xlabel('Re(z)')

ylabel('Im(z)')

Получили: