подгон 2018 (легендарный) / 1 курс-20241122T213915Z-001 / _2_ Физика / 2 семестр / Теория_доки / Lec8

Д

а «Ф

а. О

а. А

а

а»

М д

2.2. В

ва

ва

ва

а

Ле

8. Те

в е

е

е

О

в е

:

тепловое

излу ение, закон Кир гофа, закон Стефана-

Бол

мана, закон сме

ени

Вина, формула Р ле -Джинса, формула Планка.

3. Закон Стефана–Бол

мана и закон сме

ени

Вина.

4. Формула Р ле –Джинса.

5. Формула Планка.

1. Те

в е

е

е.

Те л

в

е

изл

е

ие

–

лектромагнитное

излу ение,

испускаемое

ве еством,

возника

ее за с ет его внутренней

нергии. Все

другие вид

све ени

(излу ени

света), возбуждаем

е за с ет л

бого другого вида нергии,

кроме теплового, наз

ва тс л минес ен ией.

Оп т показ вает,

то

единственн

м видом

излу ени , которое может

на одит с

в

равновесии

с излу а

ими

телами,

вл етс

тепловое

излу ение.

Равновесное

излу ение

устанавливаетс

в

адиабати ески

замкнутой

системе.

Допустим,

то равновесие нару

ено, и

тело

излу ает

бол

е,

ем

погло

ает.

Тогда

внутренн

нерги

будет уб

ват ,

то

умен

ит

температуру тела,

то

противоре ит

адиабати ности

систем .

Следовател но, и излу ение не будет равновесн

м.

Все

вид

л

минес ен ии

оказ

ва

тс

неравновесн

ми.

Например,

лектрол

минес ен

и

будет

продолжат с

до

те

пор,

пока

ест

рекомбиниру

ие

асти

, т.е. проис одит

про есс

иониза ии.

Об

н е

температур

практи ески не вли

т на

тот про

есс, т.е. неважно, скол ко

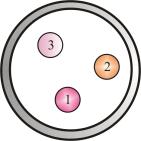
в состо ние теплового равновеси

(все

тела

и

оболо ка

будут имет одну и ту же температуру).

В

таком

состо нии

тело,

облада

ее

бол

ей

испускател ной способност , тер ет в едини у времени и

бол

е

нергии,

но T | const ,

следовател но

то

тело

должно обладат

и бол

ей погло

а

ей способност

:

Ри .1

§

rZT

·

§

rZT

·

§

rZT

·

const

(1)

¨

¸

¨

¸

¨

¸

© aZT ¹1

© aZT ¹2

© aZT ¹3

Соотно ение

(1)

в

ражает

установленн й

Кир гофом

закон,

котор

й

формулируетс

следу

им образом:

О

е ие и

ка

ел

й и

гл

а

ел

й

б

и е зави и

и

д

ела,

вл е

дл

в е

ел

д

й

и

й

же

(

иве

ал

й)

к ией

а

(дли

в л

) и

е

е а

:

rZT

f (Z,T )

(2)

aZT

Сами вели ин

rZT

и aZT

могут мен т с

при пере оде от одного тела к другому.

Отно

ение же и

оказ

ваетс

одинаков

м дл

все

тел.

Это озна ает,

то тело,

сил нее погло

а

ее какие-либо лу и, будет

ти лу и сил нее и испускат .

Дл

абсол

тно

ерного

тела

по

определени

aZT { 1.

Следовател но,

из

формул

(2)

в текает,

то

rZT

дл

такого

тела равно

f (Z,T ) . Таким образом

универсал на

функ и

Кир гофа

f Z,T ест

ни

то иное,

как испускател на

способност абсол

тно

ерного тела.

Равновесна

плотност

нергии

излу ени

св зана

с

нергети еской

светимост

абсол

тно

ерного тела соотно

ением:

f (Z,T )

c

u(Z,T ) .

4

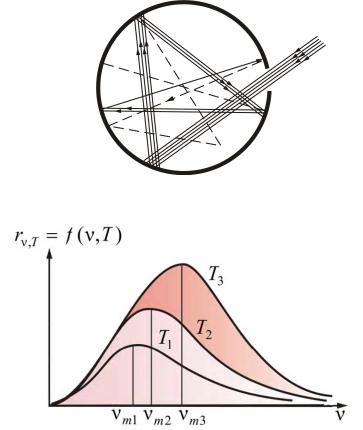
Абсол тно

ерн

тел в природе не су

ествует. Однако

полост

с

мал

м

отверстием о ен

близка по своим свойствам к

абсол

тно

ерному телу. Лу ,

попав ий внутр , после многократн

отражений

об зател но погло

а-

етс , при

м лу

л

бой

астот .

Испускател на

способност

такого

устройства

(полости) о ен

близка

к

f (Z,T ) .

Таким

образом,

если

стенки

полости

поддержива

тс

при

температуре

T,

то

из

отверсти

в

одит

излу ение вес ма близкое по

спектрал ному составу к излу ени

абсол тно

ерного тела при той же температуре.

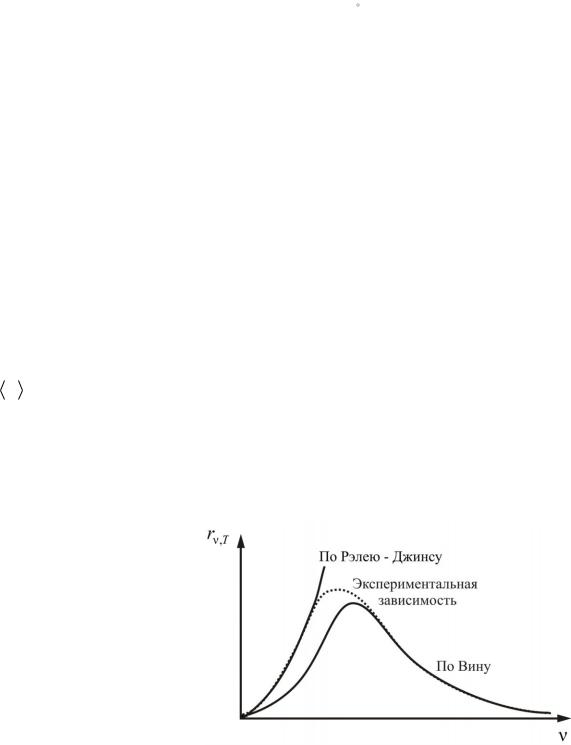
Разлага

то

излу ение в спектр, можно

найти

кспериментал н

й

вид

функ ии f (Z,T ) или f (v,T ) (рис.

3),

при

разн

температура

Т3 > Т2 > Т1.

Ри .2

Пло

ад ,

о ват

ваема

кривой,

дает

нергети еску

светимост

абсол

тно

ерного тела

при соответству

ей температуре.

Это

говорит

о

том,

то

нергети еска

совместимост

сил но зависит от температур .

Ри .3

Максимум излу ени

(излу ател ной способности) с увели ением температур

сме аетс

в сторону бол

и

астот.

3. За

С е а а–Б

а а

а

е е

В а.

Австрийский

физик

И.Стефан

в

1879

году,

анализиру

кспериментал н

е

данн е,

при ел

к

в воду,

то

нергети еска

светимост

л

бого тела пропор ионал на T 4 .

Позднее

Л

двиг Бол

ман,

применив

термодинами еский

метод

к

исследовани

ерного излу ени ,

показал,

то

то справедливо

тол ко дл

абсол

тно

ерного тела.

R*

³0f f (Z,T )dZ

VT 4

(3)

Где V

- посто нна

вели ина, T - термодинами еска

температура.

Соотно

ение

между

нергети еской

светимост

абсол тно

ерного

тела и

его

термодинами еской температурой полу ило название зак

а С

е

а а-Б л

а а.

Константу V наз ва т

й С е

а а-Б л

а а. Ее

кспериментал н е

зна ение равно

8

ª

В

º

V

5, 7 10

«

» .

2

К

4

¬ м

¼

Неме кий у ен

й Вил гел м Вин установил соотно

ение дл

Om :

T Om

b ,

которое наз

ваетс

зак

е

е и

Ви а.

Экспериментал ное зна ение констант

b равно

b

2.90 10 3 м К

2,90 107 A K

4. Ф

а Р

е –Дж

а.

В 1900 году Р лей подо

л к изу ени спектрал н

закономерностей

излу ени

ерного тела с пози

ии статисти еской физики

воспол зовав

ис

класси еским законом равномерного распределени

нергии

по

степен м

свобод .

К сто

им волнам, образу

имс

в промежутке между двум

стенками, Р лей

применил один из основн

законов статисти еской физики – закон о равномерном

распределении

нергии

между

степен ми

свобод

систем ,

на од

ейс

в

равновесии.

В 1905 году Джинс уто нил рас ет

Р ле

и полу ил,

то на кажду

сто

у

волну в

среднем при одитс

нерги

kT (колебател на степен

свобод ).

dU

du E

Z2kT dZ

(где

UZ (UO )

-

спектрал на

плотност

излу ени ,

dU

-

kT

c3T

uZ

нерги

едини

об ема

излу ени

с

астотами

f

ª Дж º

(Z,Z dZ) , dU UZ dZ UO dO U ³0

UZ dZ «

» )

м

3

¬

¼

Следовател но,

окон ател но

uZ

Z2

kT

(4)-

формула

c S

2

3

Р ле -Джинса

При

мал

астота

Z

оро

ее согласие с

оп

том,

но

при бол

и

астота

– резкое

рас ождение

–

«ул трафиолетова

катастрофа»

Ри .4

5. Ф

а П а

а.

В свои

рас ета

Планк

в

брал

наиболее

просту

модел

излу а

ей

систем

(стенок полости) в виде гармони ески

ос

илл торов

(

лектри ески

диполей) со всевозможн ми собственн

ми

астотами.

Здес

Планк

следовал

Р ле

.

Но

Планку

при ла м сл

св зат

с

нергией ос

илл тора не его

температуру, а его

нтропи .

Оказалос ,

то

полу енное

в ражение

оро

о

опис

вает

кспериментал н

е

данн е (окт бр

1900

г.). Однако обосноват

сво

формулу Планк смог тол ко в декабре 1900 года, после того, как более глу

боко

пон л веро тностн й

см

сл

нтропии,

на

котору

указал

Бол

ман

( S

k ln :).Термодинами еска

веро тност

:

–

исло

возможн

микроскопи ески

комбина ий,

совместимое с данн

м состо нием в

елом.

В

данном слу ае

то

исло возможн

способов распределени

нергии между

ос илл торами. Однако, такой про есс подс ета возможен, если

нерги

будет

принимат

не

л

б

е непрер вн е зна ени ,

а

ли

дискретн

е

зна ени ,

кратн

е некоторой

едини ной

нергии. Эта

нерги

колебател ного движени

должна б т

пропор ионал на астоте.

Ги

еза Пла ка: Излу ение и погло

ение света ве

еством проис одит не

непрер

вно, а коне н

ми пор и ми,

наз

ваем

ми квантами света или квантами

нергии. Энерги

в полости может принимат

тол ко дискретн е зна ени : 0 ,

E0 ,

2E0 , ..., nE0 .

Минимал на

пор и

нергии E0

Z , где

1, 05 10 34 Дж .

Прин ипиал ное отли ие в

вода Планка от в

водов Р ле

и други

в том,

то

«не может

б

т

и

ре и

о

равномерном

распределении

нергии

между

ос илл торами».

То,

то E0

Z –

то гениал на

догадка Макса Планка

Тогда (в

вод опу

ен) формула Планка будет в

гл дет

следу

им образом:

uZ

Z3

§

1

·

(5)

¨

¸

3

2

Z

¨

¸

c S

© e

kT 1 ¹

Формула Планка

оро о согласуетс

с

кспериментом, следовател но,

из нее

в

текает закон Стефана-Бол

мана и формула Вина.

Лек ионн

е демонстра ии

Показ комп

терной демонстра ии.

Изл

е ие аб

л

е г

ела

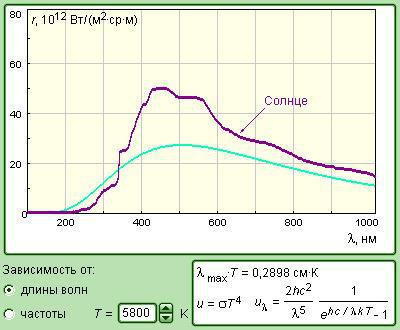
Комп терна модел (рис.5)

предназна ена дл

изу ени

спектрал ного

состава

излу ени

абсол тно

ерного

тела

при

разли н

температура

T.

рису тс

графики

спектрал ной

светимости r(O,T ) или r(v,T )

(в

относител н

едини а ).

Ри .5

Пере од от

астот к длинам волн и обратно осу

ествл етс при помо и кнопок

астота и длина волн .

Температуру

ерного тела можно измен т в интервале от 3500 К до 7000 К.

При изменении температур

график поднимаетс

или опускаетс , измен свой

вет, котор й соответствует длине волн λmax.

У еб - е

д е

е

а е а

О

в а

е а

а

вузов.- М.: Бином. Лаборатори базов

знаний, 2007.

6.

Лосев В.В., Морозова Т.В. Оптика. Лабораторн

й практикум по курсу

об ей физики. «Оптика» - М.: МИЭТ, 2008. (Част 1,

аст

2).

7.

Берестов А.Т., Боргардт Н.И., Куклин С.Ю. Лабораторн

е работ по

курсу об

ей физики «Строение ве

ества». - М.: МИЭТ, 2007.

8.

Кала ников Н.П., Кожевников Н.М. Физика.

Интернет

тестирование

Базов

знаний: у ебное пособие. – СПб.: Лан , 2009. – 160 с.

Д

е

а

е а

а

Пе е е

е

в е «И е е »

Пе е е

а

е

г

1. Корпоративна информа ионно-те нологи еска

платформа ОРИОКС -

http://orioks.miet.ru