подгон 2018 (легендарный) / 1 курс-20241122T213915Z-001 / _2_ Физика / 1 семестр / Лекции / Lec8

Лекция 8. Первое начало термодинамики

Лекция 8 Первое начало термодинамики

§8.1. Распределение Больцмана и барометрическая формула.

Если газ находится во внешнем силовом поле, то концентрация его молекул в разных областях пространства будет разной. Выведем формулу зависимости концентрации от координат: . Если нам удастся рассчитать долю молекул газа, находящихся внутри объёма dxdydz в точке с координатами (x,y,z), то задачу можно считать решенной. На прошлой лекции мы уже получили нужную нам формулу, но только в пространстве скоростей:

Оказывается, что распределение молекул по скоростям полностью определяется кинетической энергией молекулы, которая, собственно, и является функцией скорости. Очевидно, что за распределение молекул по координатам должна отвечать энергия, являющаяся функцией координат молекулы, а именно – потенциальная энергия . Более того, соответствующая формула оказывается той же самой!!!

► Функция плотности вероятности распределения молекул во внешнем поле называется распределением Больцмана.

Из полученной нами формулы легко перейти к концентрациям:

Эта формула позволяет рассчитывать концентрацию газа, находящегося в равновесии в произвольном внешнем силовом поле, например, в электростатическом или сил инерции.

Барометрическая формула

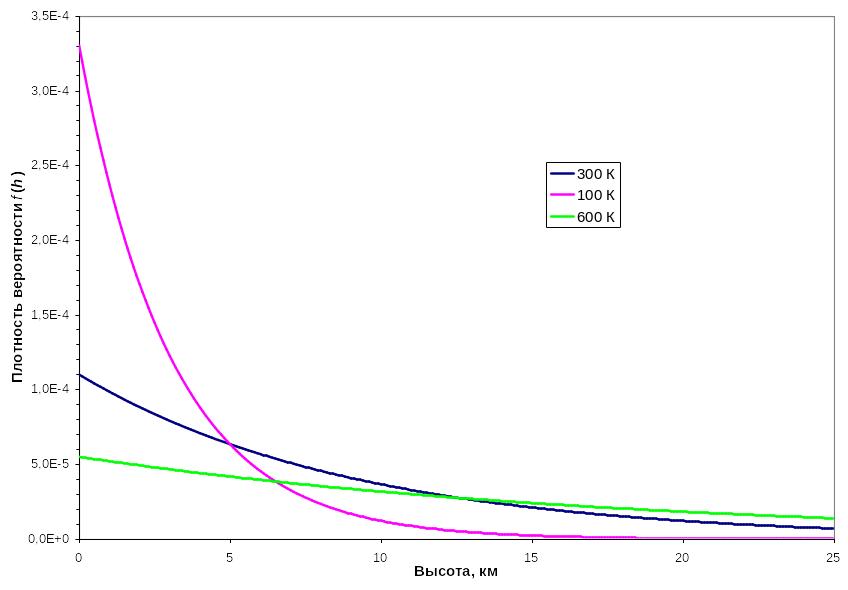
Рассмотрим идеальный газ во внешнем гравитационном поле . Поскольку при нормальных условиях воздух можно считать идеальным газом, эта модель описывает земную атмосферу. Будем считать, что температура газа по всей высоте столба одинакова. Распределение Больцмана в этом случае принимает вид: . На рисунке показан график этой функции для азота при различных температурах. Анализ графика показывает, что распределение Больцмана возникает в результате противоборства двух тенденций:

• Притяжение молекул к Земле стремится расположить их у её поверхности;

• Тепловое движение стремится разбросать молекулы равномерно по высоте.

Изменение концентрации с высотой приводит к изменению давления:

► Барометрическая формула – зависимость атм. давления от высоты:

Барометрическая формула может быть выведена непосредственным интегрированием условия равновесия газа в поле силы тяжести. Этот вывод не входит в программу данного курса. Те, кому интересно, как это делается, могут посмотреть в учебнике Савельева (Термодинамика) §1.14.

§8.2. Первое начало термодинамики

Термодинамическое описание основывается на постулировании небольшого числа начал термодинамики, из которых затем выводится большое количество следствий, позволяющих решать различные практические задачи. Исторически термодинамика возникла при попытках объяснить теоретически работу тепловых двигателей, которые, в свою очередь, были придуманы в процессе поисков вечного двигателя.

► Вечный двигатель 1-го рода: машина, совершающая работу без затрат энергии.

С точки зрения физики возможность существования вечного двигателя первого рода противоречит закону сохранения энергии. Поэтому после многих безуспешных попыток его создания было сформулировано первое начало термодинамики, согласно которому в любом тепловом процессе не должен нарушаться закон сохранения энергии.

► Первое начало термодинамики: «Тепло, поступившее в систему, расходуется на увеличение её внутренней энергии и на совершение работы»

► Физический смысл: Это закон сохранения энергии для тепловых процессов.

Внутренняя энергия

В состав внутренней энергии входят:	В состав внутренней энергии не входят:
Кинетическая энергия хаотического движения молекул (поступательная, вращательная и колебательная). Потенциальная энергия взаимодействия молекул системы. Внутренняя энергия молекул, атомов, ядер.	Потенциальная энергия во внешнем поле Кинетическая энергия движения тела как целого

Экспериментально установлено, что внутренняя энергия пропорциональна температуре.

► Функция состояния в заданном равновесном состоянии имеет вполне определённое значение, независимое от того, каким путём система в это состояние приведена.

• Примеры функций состояния: давление, объём, температура.

• Внутренняя энергия – функция состояния.

• Работа и количество теплоты не являются функциями состояния.

Поэтому в дифференциальной форме первое начало термодинамики записывают:

Работа идеального газа

Теперь первое начало термодинамики можно записать в виде:

§8.3. Теплоёмкость

► Теплоёмкость – физическая величина, численно равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на 1K:

• Если теплоёмкость не зависит от температуры, можно от бесконечно малых приращений перейти к конечным:

• Удельная теплоёмкость :

• Молярная теплоёмкость C:

Их взаимосвязь:

Теплоёмкость в различных процессах

1. Изохорический процесс: .

► Теплоёмкость при постоянном объёме:

из первого начала термодинамики получим . Подставим в определение теплоёмкости при постоянном объёме:

Тогда, если считать теплоёмкость не зависящей от температуры, можно с точностью до неопределённой константы считать:

2. Изобарический процесс: .

► Теплоёмкость при постоянном давлении:

Тогда первое начало термодинамики примет вид: .

Пусть у нас имеется один моль газа . Тогда уравнение состояния примет вид:

Подставив выражение для и заменив теплоёмкости на молярные, получим:

► Уравнение Майера:

Постоянная адиабаты

► Постоянной адиабаты (показателем адиабаты) называется величина

Величина показателя адиабаты различных газов обычно приводится в таблицах. Зная её, можно легко рассчитать обе теплоёмкости – при постоянном давлении и при постоянном объёме:

;

Если теплоёмкость не зависит от температуры, то: ;

Численные значения теплоёмкостей при постоянном давлении и постоянном объёме можно найти из молекулярно-кинетической теории.

Теплоёмкость и степени свободы молекулы.

Молекулы идеального газа не притягиваются и не отталкиваются, а значит, их энергия взаимодействия равна нулю, и внутренняя энергия газа равна сумме энергий молекул. Для 1 моля:

где – средняя кинетическая энергия молекулы. В неё входят:

• Энергия поступательного движения (о ней мы говорили при расчете давления газа)

• Энергия вращения молекулы;

• Энергия колебательного движения.

► Число степеней свободы – количество независимых величин, необходимых для задания положения тела в пространстве.

Формулу для поступательной части энергии мы уже получили ранее:

С поступательным движением связаны 3 степени свободы молекулы (вперед-назад; вправо-влево; вверх-вниз – 3 координаты). Таким образом, на одну поступательную степень свободы приходится энергия . Этот факт является проявлением важнейшего закона:

► Закон равнораспределения энергии по степеням свободы: на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия .

При этом имеются в виду не только поступательные, но и вращательные и колебательные степени свободы. Обозначим: i – полное число степеней свободы молекулы. Тогда:

С другой стороны,

Сравнив с выражением внутренней энергии через степени свободы, получим:

1. Одноатомный газ (инертные газы – He, Ne, Ar, Xe): i=3 (все поступательные)

2. Двухатомный газ (H₂, O₂, N₂): i=5 (3 поступательных и 2 вращательных)

3. Сложные молекулы (H₂O, CO₂ и т.п.): i=6 (3 поступательных и 2 вращательных)

§8.4. Работа идеального газа в различных процессах

Работу, совершаемую газом, рассчитывают по формуле

• И зохорный процесс:

• И зобарный процесс:

• Изотермический процесс Зависимость можно найти из уравнения состояния: .

Если выразить объём через давление из уравнения состояния, получим:

Адиабатический процесс.

► Адиабатический процесс происходит без теплообмена с окружающей средой.

► Уравнение адиабаты (уравнение Пуассона): (без вывода).

Это уравнение можно записать и в других переменных, исключив давление с помощью уравнения состояния:

П остроим график адиабаты и сравним его с изотермой.

• Уравнение изотермы:

• Уравнение адиабаты:

Пусть эти две кривые пересекаются в некоторой точке. Величина γ всегда больше единицы. Из курса математики известно, что в этом случае в точке пересечения угол наклона кривой будет больше, чем у кривой .

Работу газа для адиабатического процесса проще всего выразить через температуру:

Литература

Л-2. И. Е. Иродов. Физика макросистем. Основные законы: Учеб. пособие для вузов / Иродов И.Е.. - 4-е изд.. - М. : Бином. Лаборатория знаний, 2010. - 207 с.

Л-8. И. В. Савельев. Курс общей физики: Учеб. пособие для втузов: В 5-ти кн.. Кн. 3 : Молекулярная физика и термодинамика / Савельев И.В.. - М. : Астрель : АСТ, 2007. - 208 с.

8-5

Модуль 1.2 Термодинамика