Новый документ
.docxЛабораторна робота №7. Графічний метод розв'язування ЗЛП
Виконала:
Студентка 3 курсу, 1 групи
Економіка підприємства
Стешенко Тетяна
Тема: Графічний метод розв’язування ЗЛП Мета: оволодіти графічним методом розв’язку задач лінійного програмування. Завдання: побудувати задачу за алгоритмом графічного методу за варіантами. Методичні рекомендації:
На основі отриманих знань на Лекції та теоретичного матеріалу даного курсу, інформаційних джерел!!!:
1.Ознайомитися з поняттям п – вимірного простору (основних змінних задачі лінійного програмування).
2.Згадати, що означає геометрична інтерпретація обмежень-рівнянь та обмежень-нерівностей.
3.Ознайомитися (вивчити) поняття вектора-нормалі (вектора-градієнта, направляючого вектора).
4.Зрозуміти інтерпретацію лінійної форми (цільової функції) задачі як лінії рівня або гіперплощини рівня.
5.Навчитися знаходити область допустимих розв’язків задачі, далі вершин ОДР.
6. Знайти оптимальні розв’язки (max, min) задачі лінійного програмування
Розв’язати графічно задачу
1) Побудувати ОДР;
2) Провести вектор-градієнт;
3) Провести лінію рівня через початок координат та через точку екстремуму (якщо така існує);
4) Якщо задача не має розвязку - вказати причину;
5) Знайти координати точки екстремуму;
5) Написати відповідь.
Варіант
1
Крок №1. Побудуємо область допустимих рішень, тобто графічно розв'яжемо систему нерівностей. Для цього побудуємо кожну пряму і визначимо півплощини, задані нерівностями (півплощини позначені штрихом).
Побудуємо
рівняння
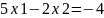 за двома точками. Для знаходження першої
точки прирівнюємо
за двома точками. Для знаходження першої
точки прирівнюємо
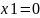 .
Знаходимо
.
Знаходимо
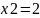 .
Для знаходження другої точки прирівнюємо
.
Для знаходження другої точки прирівнюємо
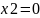 .
Знаходимо
.
Знаходимо
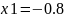 .
Поєднуємо точку
.
Поєднуємо точку
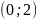 з
з
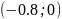 прямою лінією. Визначимо півплощину,
задану нерівністю. Обравши точку (0; 0),
визначимо знак нерівності в півплощині:
прямою лінією. Визначимо півплощину,
задану нерівністю. Обравши точку (0; 0),
визначимо знак нерівності в півплощині:
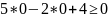 ,
тобто
,
тобто
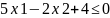 в півплощині вище прямої.
в півплощині вище прямої.
Побудуємо
рівняння
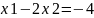 за двома точками. Для знаходження першої
точки прирівнюємо
.
Знаходимо
.
Для знаходження другої точки прирівнюємо
.
Знаходимо
за двома точками. Для знаходження першої
точки прирівнюємо
.
Знаходимо
.
Для знаходження другої точки прирівнюємо
.
Знаходимо
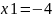 .
Поєднуємо точку
з
.
Поєднуємо точку
з
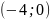 прямою лінією. Визначимо півплощину,
задану нерівністю. Обравши точку
прямою лінією. Визначимо півплощину,
задану нерівністю. Обравши точку
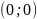 ,
визначимо знак нерівності в півплощині:
,
визначимо знак нерівності в півплощині:
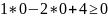 ,
тобто
,
тобто
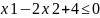 в півплощині вище прямої.
в півплощині вище прямої.
Побудуємо
рівняння
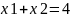 за двома точками. Для знаходження першої
точки прирівнюємо
.
Знаходимо
за двома точками. Для знаходження першої
точки прирівнюємо
.
Знаходимо
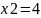 .
Для знаходження другої точки прирівнюємо
.
Знаходимо
.
Для знаходження другої точки прирівнюємо
.
Знаходимо
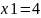 .
Поєднуємо точку
.
Поєднуємо точку
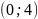 з
з
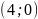 прямою лінією. Визначимо півплощину,
задану нерівністю. Обравши точку (0; 0),
визначимо знак нерівності в півплощині:
прямою лінією. Визначимо півплощину,
задану нерівністю. Обравши точку (0; 0),
визначимо знак нерівності в півплощині:
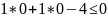 ,
тобто
,
тобто
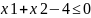 в півплощині нижче прямої.
в півплощині нижче прямої.
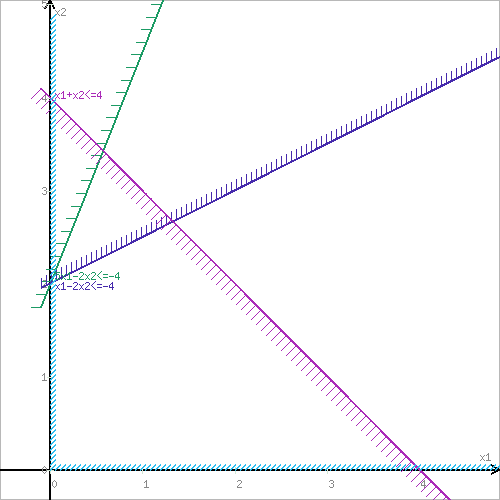
Графік 1
Або

Графік 2
Крок №2. Межі області допустимих рішень.
Перетином півплощин буде область, координати точок якої задовольняють умову нерівностям системи обмежень задачі.
Позначимо межі області багатокутника рішень.

Графік 3
Крок
№3. Розглянемо цільову функцію задачі
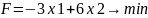 .
.
Побудуємо
пряму, що відповідає значенню функції
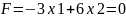 .
Вектор-градієнт, складений з коефіцієнтів
цільової функції, вказує напрямок
максимізації
.
Вектор-градієнт, складений з коефіцієнтів
цільової функції, вказує напрямок
максимізації
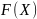 .
Початок вектора – точка
,
кінець – точка
.
Початок вектора – точка
,
кінець – точка
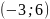 .
Будемо рухати цю пряму паралельним
чином. Оскільки нас цікавить мінімальне
рішення, тому рухаємо пряму до першого
дотику вказаної області. На графіку ця
пряма позначена пунктирною лінією.
.
Будемо рухати цю пряму паралельним
чином. Оскільки нас цікавить мінімальне
рішення, тому рухаємо пряму до першого
дотику вказаної області. На графіку ця
пряма позначена пунктирною лінією.
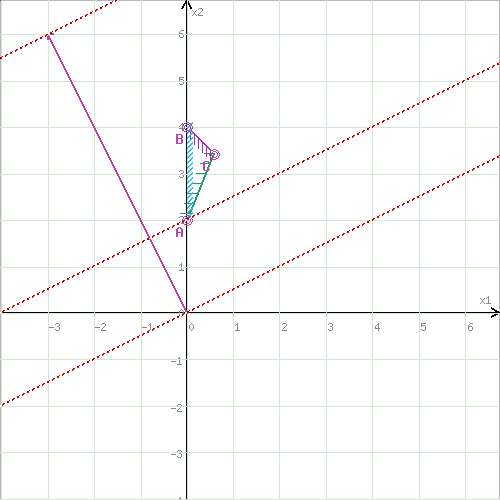
Графік 4
Пряма
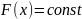 перетинає область в точці
перетинає область в точці
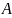 .
Оскільки точка
отримана в результаті перетину прямих
.
Оскільки точка
отримана в результаті перетину прямих
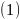 і
і
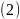 ,
то її координати задовольняють рівнянням
цих прямих:
,
то її координати задовольняють рівнянням
цих прямих:
Розв'язавши систему рівнянь, отримаємо: ,
Звідки знайдемо мінімальне значення цільової функції: