Новый документ (3)

Лабораторна робота №3. Складання задач лінійного програмування та зведення їх до стандартної форми

Виконала:

Студентка 3 курсу, 1 групи

Економіка підприємства

Стешенко Тетяна

Тема: Складання задач лінійного програмування та зведення їх до стандартної форми. Мета:вміти застосовувати отримані знання для зведення їзадачі  до стандартної форми за варіантами.  Методичні рекомендації: 1. Вхідні знання та навички отримати з теоретичного матеріалу та практичних занять реалізувати, сзавдання 2. Звести задачу до стандартної форми.

21 Варіант

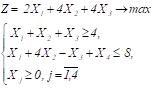
У першому нерівності зі знаком (≥) вводимо базисну змінну x5 зі знаком мінус. У другому нерівності зі знаком (≤) вводимо базисну змінну x6.

Перехід к СЗЛП.

Розширена матриця системи обмежень-рівностей даної задачі:

1	1	1	0	-1	0	4
1	4	-1	1	0	1	8

Приведемо систему до одиничної матриці методом жорданових перетворень.

1. В якості базової змінної можна вибрати x5. Отримуємо нову матрицю:

Отримаємо нову матрицю:

-1	-1	-1	0	1	0	-4
1	4	-1	1	0	1	8

2. В якості базової змінної можна вибрати x6.

Оскільки в системі є одинична матриця, то в якості базисних змінних приймаємо X = (5,6). Відповідні рівняння мають вигляд:

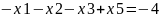
Виразимо базисні змінні через інші:

Підставимо їх у цільову функцію:

Система нерівностей:

Приведемо систему нерівностей до наступного вигляду:

Спростимо систему.

Якщо задача ЛП розв’язується на пошук мінімального значення, то стандартна форма матиме наступний вигляд:

Перехід к КЗЛП.

Для приведення ЗЛП до канонічної форми необхідно:

1. Змінити знак у цільовій функції. Зведемо задачу F(X) → min до задачі F(X) → max.

Для цього помножимо F(X) на (-1).

У першому нерівності зі знаком (≤) вводимо базисну змінну x4. У другому нерівності зі знаком (≥) вводимо базисну змінну x5 зі знаком мінус.

Цільова функція для вирішення задачі на min:

Перехід до СЗЛП.

Розширена матриця системи обмежень-рівностей даної задачі:

1	2	3	1	0	12
4	8	3	0	-1	24

Приведемо систему до одиничної матриці методом жорданових перетворень.

1. В якості базової змінної можна вибрати x4.

2. В якості базової змінної можна вибрати x5.

Отримуємо нову матрицю:

1	2	3	1	0	12
-4	-8	-3	0	1	-24

Оскільки в системі є одинична матриця, то в якості базисних змінних приймаємо X = (4,5).

Відповідні рівняння мають вигляд:

Виразимо базисні змінні через інші:

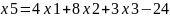
Підставимо їх у цільову функцію:

Система нерівностей:

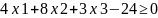
Приведемо систему нерівностей до наступного вигляду:

Спростимо систему.

Якщо задача ЛП розв’язується на пошук максимального значення, то стандартна форма матиме наступний вигляд: