Новый документ (1)

Лабораторна робота №8. Симплексний метод розв'язку ЗЛП

Виконала:

Студентка 3 курсу, 1 групи

Економіка підприємства

Стешенко Тетяна

Тема: Симплексний метод розв’язку ЗЛП Мета: Оволодіти універсальним методом розв’язку задач лінійного програмування.

 

Завдання: забезпечити формування практичних навичок розв’язку задач лінійного програмування універсальним симплексним методом.

Виконати роботу за варіантами,дотримуючись наступних методичних рекомендацій:

1.Вивчити алгоритм повних виключень Жордана-Гауса для розв’язування системи лінійних алгебраїчних рівнянь

2.Згадати систему лінійних алгебраїчних рівнянь розміром m ×n

3. Ознайомитись та вивчити алгоритм (по крокам) розв’язку системи лінійних алгебраїчних рівнянь.

4 .Навчитися знаходити базисний розв’язок системи лінійних алгебраїчних рівнянь, залежних (базисних) та незалежних (небазисних) змінних

5. Вивчити алгоритм розв’язку системи лінійних алгебраїчних рівнянь у спеціальних повних таблицях, правило прямокутника.

4. Навчитися знаходити «розв’язуючий елемент», рядка та колонки (стовпчика).

5. Знайти загальний, частинний (окремий) розв’язки системи лінійних алгебраїчних рівнянь

Варіант 1

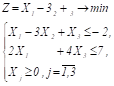
Розв’яжемо пряму задачу лінійного програмування симплексним методом, використовуючи симплексну таблицю. Оскільки в правій частині присутні від’ємні значення, помножимо відповідні рядки на (-1). Визначимо мінімальне значення цільової функції 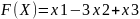за наступних умов-обмежень:

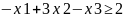
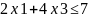
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних (перехід до канонічної форми).

У 1-му нерівності смислу (≥) вводимо базисну змінну x4 зі знаком мінус.

У 2-му нерівності смислу (≤) вводимо базисну змінну x5.

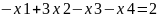
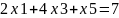
Розширена матриця системи обмежень-рівностей даної задачі:

-1	3	-1	-1	0	2
2	0	4	0	1	7

Приведемо систему до одиничної матриці методом жордановських перетворень.

1. В якості базової змінної можна вибрати x4.

Отримуємо нову матрицю:

1	-3	1	1	0	-2
2	0	4	0	1	7

2. В якості базової змінної можна вибрати x5. Оскільки в системі є одинична матриця, то в якості базисних змінних приймаємо .

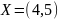Виразимо базисні змінні через інші:

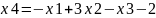
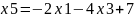
Підставимо їх у цільову функцію:

Серед вільних членів є від’ємні значення, отже, отриманий базисний план не є опорним.

Замість змінної x4 слід ввести змінну x2. Виконуємо перетворення симплексної таблиці методом Жордано-Гаусса.

Базис	B	x1	x2	x3	x4	x5
x2	2/3	-1/3	1	-1/3	-1/3	0
x5	7	2	0	4	0	1
F(X0)	2	0	0	0	-1	0

Представимо розрахунок кожного елемента у вигляді таблиці:

B	x1	x2	x3	x4	x5
-2 : -3	1 : -3	-3 : -3	1 : -3	1 : -3	0 : -3
7-(-2*0):-3	2-(1*0):-3	0-(-3*0):-3	4-(1*0):-3	0-(1*0):-3	1-(0*0):-3

Виразимо базисні змінні через інші:

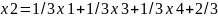
Підставимо їх у цільову функцію:

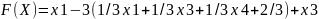
або

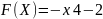
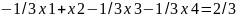
При обчисленні значення 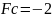тимчасово не враховуємо. Матриця коефіцієнтів 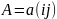цієї системи рівнянь має вигляд:

A =

-1/3	1	-1/3	-1/3	0
2	0	4	0	1

Базисні змінні це змінні, які входять тільки в одне рівняння системи обмежень і при цьому з одиничним коефіцієнтом.

Економічний сенс додаткових змінних: додаткові змінні задачі ЛП позначають надлишки сировини, часу, інших ресурсів, що залишаються в виробництві даного оптимального плану.

Розв’яжемо систему рівнянь відносно базисних змінних: x2, x5 Припускаючи, що вільні змінні дорівнюють 0, отримуємо перший опорний план:

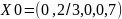
Базисне рішення називається допустимим, якщо воно не від’ємне.

Базис	B	x1	x2	x3	x4	x5
x2	2/3	-1/3	1	-1/3	-1/3	0
x5	7	2	0	4	0	1
F(X0)	0	0	0	0	1	0

Переходимо до основного алгоритму симплекс-метода.

Кінцевий варіант симплекс-таблиці:

Базис	B	x1	x2	x3	x4	x5
x2	2/3	-1/3	1	-1/3	-1/3	0
x5	7	2	0	4	0	1
F(X1)	0	0	0	0	1	0

Останній рядок містить додатні елементи. Простір допустимих рішень необмежений. Рішення не існує.