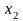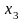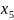лаб 1, Стешенко

Лабораторна робота №1. Побудова задач математичного програмування

Виконала:

Студентка 3 курсу, 1 група

Економіка підприємства

Стешенко Тетяна

Мета: опанування методами формалізації загальних задач лінійного програмування Завдання: забезпечити формування вмінь та навичок формалізації економічної інтерпретації задач оптимального використання ресурсів.

Ознайомитися з теоретичним матеріалом (Лекція1) виконати Ваші завдання  по варіантах інформаційної характеристики, записати свою постановку задачу.

Методичні рекомендації:

1. Записати постановка задачі оптимального використання ресурсів, визначити обмеження та критерій оптимізації.

2. Записати у векторно-матричному вигляді та розгорнутому вигляді.

3. Надати інформаційну характеристику задачі.

4. Побудувати розгорнуту числову економіко-математичну модель.

Економіко-математична модель задачі матиме вигляд:

Для виготовлення чотирьох видів продукції використовується три види сировини. Надати свою постановку задачі, як показано у довідковому файлі опису роботи. Дані наведені в таблиці.

Таблиця 1

Вид сировини	Норми витрат сировини на одиницю товару					Ресурс сировини
	А	Б	В	Г	Д
ВАРІАНТ 1
1	1	2	1	3	2		18
2	1	1	2	1	2		30
3	1	3	3	2	2		40
Ціна товару	12	7	18	10	10

Структурний запис економіко-математичні моделі:

Цільова функція

Обмеження змінних

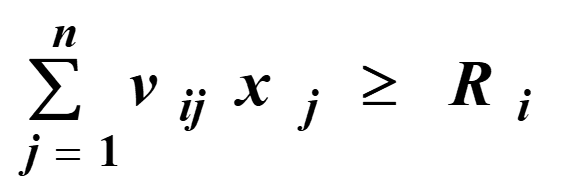
Умова невід’ємності змінних

Для побудови числової економіко-математичної моделі:

Позначимо через Х₁, Х₂ , Х₃ , Х₄ кількість продукції кожного виду:

Х₁ -кількість морозива,

Х_{2…………….}

_……., Х_{4 …………..}

Будуємо числову економіко-математичну модель задачі, яка матиме вигляд:

Ц ільова функція – це вираз, що необхідно максимізувати (в нашому випадку – загальна виручка від реалізації продукції, грош.од.):

F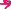 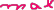( x) =12 Х₁ +7 Х₂ +18 Х₃ + 10Х₄ + 10Х_5.

Обмеження по ресурсах:

1. Використання сировини 1:

1 Х₁ + 2 Х₂ + 1 Х₃+ 3 Х₄+ 2 Х₅ <= 18.

2. Використання сировини 2:

1Х₁ + 1 Х₂ + 2 Х₃+ 1 Х₄+ 2 Х₅ <= 30.

3. Використання сировини 3:

1 Х₁ + 3 Х₂ + 3Х₃+ 2 Х₄+ 2 Х₅ <= 40.

Обмеження на знак змінних:

Х₁, Х₂ , Х₃ , Х₄ , Х₅ >=0.

Матриця задачі буде мати вигляд:

№ п/п	Умови	А	Б	В	Г	Д	Тип обмеження	Обсяг обмеження
1	1	1	2	1	3	2		18
2	2	1	1	2	1	2		30
3	3	1	3	3	2	2		40
R	Функція мети	12	7	18	10	10		max