ДМ

19. Основные понятия теории графов. Определение и разновидности графов. Способы задания графов: аналитический, геометрический, матричный. Изоморфизм графов. Примеры. 2 ЧАСТЬ

Элементы теории графа – раздел математики имеющий широкое практическое применение, в её терминах формулируется большое количество задач с дискретными объектами.

Первая работа была написана Эйлером в 1736г (Задача о кенигсбергских мостах)

Определение графа

Термин граф появился в 1936г в книге Кенига.

Пусть V не пустое множество.

Элементы множества V называют вершинами графа, а элементы Е – рёбрами графа. Число вершин графа G=(V,E)

называется его порядком. Вершины графа обозначаются по разному, можно числами, можно прописными буквами. Ребра соединяют две вершины.

Вершина, из которой выходит ровно одно ребро - такую вершину называют концевой.

Инцидентность - вершина и ребро называются инцидентными, если вершина является для этого ребра концевой.

Кратные рёбра — это два и более рёбер, инцидентных одним и тем же двум вершинам.

Простой граф – граф не содержащий кратных рёбер.

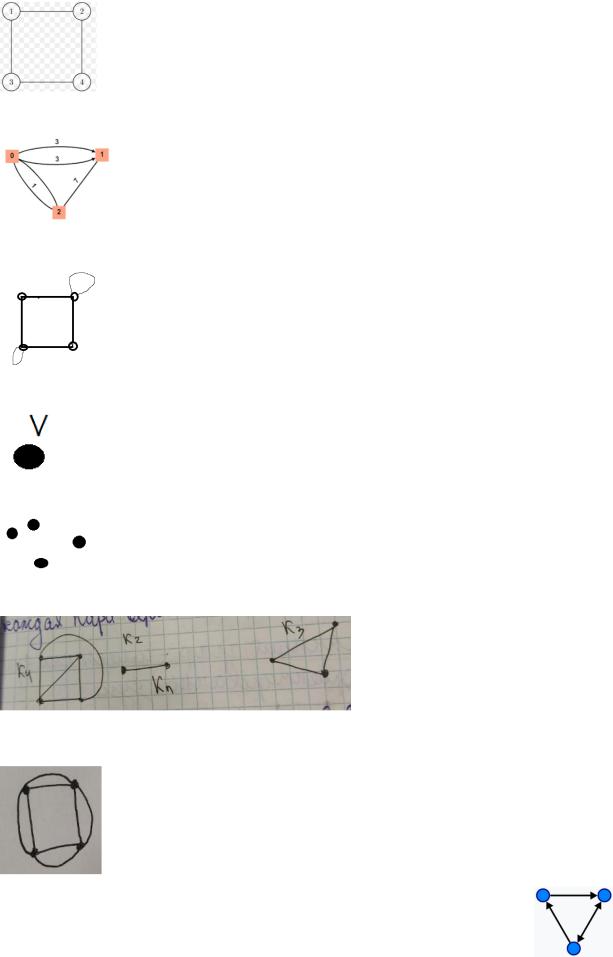
Мультиграф – простой граф с кратными рёбрами.

(0.1) и (1.0) кратные рёбра. (0.2) и (2.0) кратные рёбра

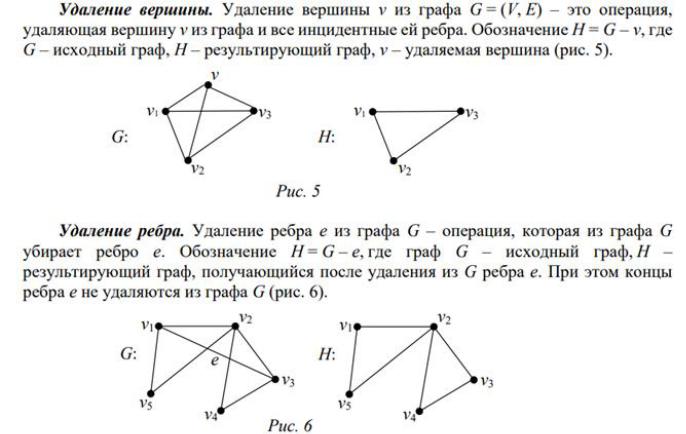
Псевдограф – граф с петлями.

Тривиальный граф – состоит из одной вершины.

Нулевой граф – это множество вершин, но рёбра в неё отсутствуют.

Полный граф – простой граф, в котором каждая пара вершин – смежны(связаны). Каждая вершина связана с другой.

Правильный граф – степени всех вершин между собой равны. В каждую вершину входит одинаковое количество ребёр.

Ориентированный граф (кратко орграф) —граф, рёбрам которого присвоено направление.

Смешанный граф – имеет как дуги, так и ориентированные дуги.

Двудольный граф -существует способ разбить вершины на 2 подмножества так, чтобы ребра соединяли только вершины из разных подмножеств.

Граф можно задать – 1) Перечислением 2) Графически 3) Матрицей

Существуют: матрица смежности, матрица инцидентности, список ребер графа. Изоморфизм графов – два графа

G1 и G2 называются изоморфными, если между множествами их вершин существует такое взаимное однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только том случае, если в другом графе ребрами соединены соответствующие им вершины.

20. Операции над графами с примерами.

Удаление вершины, удаление ребра, добавление вершины, добавление ребра(добавляется вместе с точками), слияние вершин, стягивание ребра, расщепление вершин(одно ребро убирается появляется два новых), дополнение графа (существует граф и рядом добавляют другой граф при слиянии с этим графом – наш граф станет полным-то есть каждая вершина будет связана с другой вершиной), объединение графов(есть два графа, у них есть вершина которая одинакого называется и эти вершины слияют в одну), сумма графов (дано два графа и теперь каждая из вершин одного и другого соединены ребром), произведение графов(смотри рисунок).

Если графы

соединить получится полный граф, где каждая вершина соединяется друг с другом.

21. Маршруты, цепи, циклы. Связность. Определения и примеры. Нахождение сильных компонент орграфа. Выявление маршрутов с заданным количеством ребер.

22. Метрические характеристики графа.

23.Понятие сети. Матрица весов. Нахождение кратчайших путей в ориентированной сети с помощью алгоритма Дейкстры.

24.Нахождение кратчайших путей в ориентированной сети с помощью алгоритма Беллмана-Мура.

25.Деревья и их свойства, лес. (4 теоремы, примеры)

Дерево – связный неориент ациклический граф. Лес – граф без циклов. Свойства деревьев –